沥青针入度仪器

在今年的两会上，与会代表提出“取消重大节假日高速公路免费通行政策，与此同时，全面降低高速公路收费标准”的建议，引起了大家的热议。高速公路已经与人们出行密不可分，影响高速公路质量的重要材料——沥青。沥青乳液沥青乳液不仅使沥青的加工和储存变得简单，也使得道路的铺设过程更为方便（1）。沥青乳液的物理、化学及应用性能在很大程度上取决于沥青、乳化剂和水的含量比，以及沥青乳液的粒径分布（2）。常温下，沥青是不可加工的。因此，为了使沥青变的可加工，需采用不同的工艺对其处理。最常见的技术是将沥青加热到液态。另一种技术是将沥青加工成乳状液。然而，单纯将沥青和水混合在一起并不能形成一个稳定体系。因此，要根据具体的应用需求在沥青中添加一定的稳定剂和乳化剂。沥青乳液使用起来非常方便，同时也更容易对其储存、运输和进一步加工。沥青乳液的优势及化学组成沥青乳液的优势：良好的润湿能力低能源消耗和环境友好可通过增塑剂对其改性状态的多样性(如粘度)沥青乳液的化学组成：在沥青乳液中，沥青为分散相，水为连续相。为了保证能够乳化充分并形成稳定的颗粒，对乳化剂的选择变得十分重要。而粒径和乳化剂也同样会影响沥青乳液的加工性能和存储稳定性。乳化剂分子附着在沥青颗粒的表面，使这些颗粒具有均匀的电荷。这导致颗粒间的静电斥力，从而阻止乳液颗粒在运输和储存过程中固化。根据电荷(正电荷或负电荷)的不同，可以将其分为阳离子或阴离子的沥青乳液。沥青乳液的应用取决于其电荷、沥青质量分数、乳化剂、水以及沥青乳液的粒径（2）。实验实验中选取四种不同的沥青乳液(样品1 - 4)，固含量均为63%。实验分别研究了样品的粒径、电位及流变行为。电位zeta电位的测量采用安东帕Litesizer 500。样品经水稀释，pH 为8.6±0.2。实验中对电位的测量采用Ω样品池，分别对样品进行三次系列测试。Litesizer 500粒径粒径分布(PSD)采用安东帕PSA 1090 L测定。实验设置为三次系列测量，水为流动相。样品分散不需要超声处理，搅拌和泵速分别设置为中速，遮光度设为10%，并采用夫琅和费近似理论对粒度分布进行计算。PSA流变行为为了表征沥青乳状液的流变特性，采用Anton Paar公司的流变仪及其平板测量系统PP25对样品进行测试。实验中，对每个样品在25°C下的流变曲线和振幅扫描进行测量。流变曲线的剪切速率范围为0.01~100s -1，时间范围为100s~1秒。振幅扫描的角频率为10 rad / s，形变范围为0.01~100% 。SmartPave结果与讨论zeta电位对稳定性的评估通过对沥青乳液zeta电位的表征，可得到样品稳定性的相关信息。zeta电位值越高，体系越稳定。实验中的所有样品zeta电位均为负值，说明沥青乳状液为阴离子型。如表1所示。这说明热处理对沥青乳状液的稳定性没有影响。样品加工性能的表征实验中，对样品1和样品2的加工性能进行了比较。样品1比样品2的粒径分布更宽，同时包含了大颗粒和小颗粒(图1)。两个样品的D90值差异最为明显（表2）。图2显示了样品的剪切速率粘度函数。样品1的小颗粒含量较少，与样品2（小颗粒含量较多）相比其表面积较小。较小的表面积说明颗粒和液体之间较小的界面，导致两相之间的摩擦力和相互作用力较小。从而造成较低的粘度，如图2所示。样品的屈服应力也不同。样品1 (2.33 Pa)颗粒较大(图3)，其屈服应力低于样品2 (15.99 Pa)。质量控制沥青配方及工艺参数对其最终产品的粘度均有影响，为了控制产品的粘度，可在生产过程中对工艺参数进行监测。例如，样品3和样品4在粘度上没有差异，但在加工后表现出不同的流变特性（图4）。样品3的屈服应力为31.78 Pa，高于样品4的22.63 Pa。此外，样品3的损耗模量G”更高，这意味着它比样品4的粘性更大(图5)。这些结果表明，沥青乳液样品的界面性质不同，可通过测量粒度分布来实现质量控制。表3和图6汇总了各个样品的粒径结果。结论及参考文献结论实验展示了粒径对不同沥青乳液流变性能的影响。一般认为，沥青乳液的稳定性很好，同时具有以下特性：粒径越小，粘度越大粒径分布越宽，粘度越小具有混合粒径的沥青乳液，比只有单一粒径的沥青乳液粘度更低粒径分布影响样品的粘弹行为和屈服点利用现代测量技术，有利于开发出黏度相对较低但固体含量较高的高稳定性沥青乳液。沥青乳液的屈服应力和粒径分布影响着沥青乳液的应用性能，因此对这些参数的分析具有重要的意参考文献安东帕中国总部销售热线：+86 4008202259售后热线：+86 4008203230官网：www.anton-paar.cn在线商城：shop.anton-paar.cn

无锡的陆经理，8月1日致电北京路晨伟业仪器设备有限公司，电话010-56429861,13693675139咨询沥青三大指标仪器，我公司销售员工小刘给予了陆经理详细的解释，山东和江苏这两个省份，省级要求延伸仪的温度分辨率是0.01摄氏度，经过周密的分析和讲解，陆经理采购了北京路晨伟业仪器设备有限公司的LYY-9A智能低温沥青延伸度测定仪、SZR-6加热型沥青针入度测定仪，HR-2806E电脑智能沥青软化点测定仪各一台，发货物流：江浙沪专线，发货日期：2016年8月4日，到货日期：2016年8月6日，请陆经理保持电话畅通，等待接货，期待与您的再次合作。 LYY-9A智能低温沥青延伸度测定仪 1、最大测定工作长度：1500mm2、拉伸滑板移动速度：50mm/min 和 100mm/min3、拉伸电机功率：120W 4、水浴搅拌电泵：45W5、制冷功率：1.5KW6、水浴温度控制范围：5---50℃ 7、控温精度：±0.1℃ 温度分辨率：0.01℃ 8、制冷量：4000卡/min 9、工作电源电压：220V

2010年10月21日-23日， 美国TA仪器作为主要赞助商参加了中国第五届沥青国际峰会， 在此次会议上美国TA仪器向广大沥青行业的客户介绍以及展示了TA仪器的沥青行业的专业级流变仪AR-G2。 .AR-G2专业的沥青流变仪从96年推出一来，现在在全球已经被几百家公司选用，区别于一般流变仪，TA沥清流变仪保持了TA流变仪一贯优点的同时，提供有专用的沥清加热水槽，专用标准油，沥青样品盘，专业的中英文分析及操作软件、专业的沥青分析引导软件等。能满足美国联邦高速公路局指定，用于对高等级公路沥青进行分级的流变分析和研究。 参会者对TA仪器这款沥青流变仪都表示出了极大的兴趣。

沥青的三大指标测定沥青耐老化性能方法一、实验目的测定沥青的耐老化性能，评估其在使用过程中的稳定性和耐久性。二、实验原理通过模拟沥青在自然环境中的老化过程，如加热、光照、氧化等，然后测定老化前后沥青的物理和化学性质的变化，来评价其耐老化性能。三、实验设备和材料1.老化箱：能够模拟不同的老化条件，如热老化、紫外老化等。2.沥青样品：不同类型和来源的沥青。3.针入度仪：用于测定沥青的针入度。4.软化点测定仪：测定沥青的软化点。5.延度仪：测量沥青的延度。6.薄膜烘箱：用于热老化试验。7.旋转薄膜烘箱：模拟沥青在实际使用中的老化过程。8.电子天平：精确称量沥青样品。9.烧杯、玻璃棒、镊子等实验室常用器具。四、实验步骤1.样品准备 选取具有代表性的沥青样品，确保样品的均匀性。 将沥青样品加热至流动状态，以便进行后续的实验操作。2.热老化试验 使用薄膜烘箱或旋转薄膜烘箱对沥青样品进行热老化处理。设定老化温度和时间，一般温度为 163℃，时间为 5 小时或更长，具体根据实际需求确定。 在老化过程中，定期观察沥青样品的状态，确保老化条件的稳定性。3.紫外老化试验 将沥青样品放置在紫外老化箱中，设定合适的紫外辐射强度和时间。 观察沥青样品在紫外辐射下的变化，如颜色、硬度等。4.物理性能测定 针入度测定：使用针入度仪测定老化前后沥青的针入度。将一定质量的标准针在规定的温度和时间内垂直刺入沥青样品中，测量针入的深度，以表示沥青的软硬程度。 软化点测定：采用软化点测定仪测定老化前后沥青的软化点。将沥青样品加热至一定温度，使其软化，然后测定其在特定条件下的软化温度。 延度测定：使用延度仪测量老化前后沥青的延度。将沥青样品制成特定形状的试件，在规定的温度和拉伸速度下进行拉伸，测量其断裂时的伸长长度。5.化学性能分析 可以采用红外光谱分析、热重分析等方法，对老化前后沥青的化学结构进行分析，了解其在老化过程中的化学变化。6.数据处理与结果分析 计算老化前后沥青的物理性能指标变化率，如针入度比、软化点增值、延度保留率等。 根据化学分析结果，分析沥青在老化过程中的化学变化机制。 综合物理性能和化学性能的分析结果，评价沥青的耐老化性能。五、注意事项1.实验过程中要严格控制老化条件，确保实验结果的准确性和可靠性。2.操作仪器时要按照操作规程进行，避免因操作不当而损坏仪器或影响实验结果。3.沥青样品在加热和处理过程中要注意安全，避免烫伤和火灾等事故的发生。4.对实验数据要进行认真记录和分析，确保数据的真实性和有效性。通过以上解决方案，可以较为全面地测定沥青的耐老化性能，为沥青的选择和使用提供科学依据。测试项目老化前数据老化后数据变化率/%针入度（0.1mm，25℃）865（80-65）/80×100=18.75软化点（℃）4552（52-45）/45×100≈15.56延度（cm，10℃）3020（30-20）/30×100≈33.33质量变化（g）50.250.8（50.8-50.2）/50.2×100≈1.2针入度比（%）8572（72/85）×100≈84.71（变化为100-84.71=15.29）在这个表格中： 针入度：反映了沥青的软硬程度，针入度值越大，沥青越软。老化后针入度减小，说明沥青经过老化变得更硬。 软化点：体现了沥青的热稳定性，软化点升高表示沥青在加热时变得更不容易软化。 延度：表示沥青的塑性和韧性，延度值越大，沥青的塑性越好。老化后延度降低，说明沥青的塑性变差。 质量变化：可以反映沥青在老化过程中由于挥发、氧化等原因导致的质量变化。 针入度比：是老化后针入度与老化前针入度的比值，针入度比越大，说明沥青的抗老化性能越好。需要注意的是，具体的测试数据会因沥青的种类、老化条件、测试方法等因素而有所不同。在实际的沥青耐老化测试中，需要根据相关的标准和规范进行操作，并对测试数据进行准确的记录和分析，以评估沥青的耐老化性能。

沥青密度数字化测量石化行业中，沥青、半固体沥青、软焦油沥青是土木工程、道路工程和石油化工中重要的工业原料。质量检测最简单快速的方法是密度测量对于沥青材料的密度测量，数字式密度计相较于传统密度测量方法如比重瓶法，有多方面的优势。2018年美国材料实验协会（ASTM）发布了《用数字密度计（U型管）测量沥青、半固体沥青和软焦油沥青相对密度和密度的方法》（ASTM D8188-18）。2020-2021年间，ILS（国际实验研究组织）使用安东帕密度计DMA 4200 M 基于该标准进行了沥青密度的测量。DMA 4200 M要求和建议：原理上采用振荡U型管法，根据U型管的振荡频率计算其中样品的密度；测量池的样品中必须没有气泡，气泡会严重影响测量结果；报告中密度的准确度应达到0.3 kg/m3，实验室内的重复性标准偏差应达到0.9kg/m3；对于流动性小的样品，加热至可倾倒，但是加热时间不宜过长以防气泡混入，同时应避免局部温度下降引起凝固和堵塞；如果需要将密度转化为API值，可以参考ASTM D1250，导出合适的公式（排除玻璃膨胀系数）。沥青密度数字化测量最佳的解决方案脉冲激发法安东帕基于传统的U型振荡管法进行了改良，发明了脉冲激发法（PEMTM），提升了黏度修正的效率。得益于原理上的突破，DMA 4200 M搭载了自动气泡检测功能FillingCheckTM，能自动对测量池中的气泡发出警告。达到四位准确度和五位重复性标准偏差，满足标准中的要求。DMA 4200 M的测量池材质为哈氏合金C276，耐腐蚀、耐高温、耐高压。采用帕尔帖半导体控温，测量池最高可升温至200℃。可选配件进出样口加热附件，保证不出现局部降温导致堵塞。内置各种条件下密度与API值转换的表格，可自动将测得的密度转化为API值，并支持特殊样品自定义输入转换表。密度计系列更多石化样品的测量及自动化需求请联系安东帕安东帕中国总部销售热线：+86 4008202259售后热线：+86 4008203230官网：www.anton-paar.cn在线商城：shop.anton-paar.cn

石油沥青简介石油沥青是原油加工过程中的一种产品，在常温下是黑色或黑褐色的粘稠的液体、半固体或固体，主要含有可溶于氯仿的烃类及非烃类衍生物，其性质和组成随原油来源及生产方法的不同而变化。从元素组成上，石油沥青是由多种碳氢化合物及非金属（氧、硫、氮）衍生物组成的混合物，其元素组成主要是碳（80~87%）、氢（10~15%）；其余是非烃元素，如氧、硫、氮等（＜3%）；此外，还含有一些微量的金属元素。 从组份分析，石油沥青的主要组分是油分、树脂和地沥青质，还含2~3%的沥青碳和似碳物，还含有蜡。沥青中的油分和树脂能浸润沥青质。沥青的结构以地沥青质为核心，吸附部分树脂和油分，构成胶团。虽然目前对于沥青质的分子结构尚无定论，但是一般认为可以把沥青质分子看成是由若干个单元片所构成，每个单元片中含有一个芳环－环烷环系，分之中单元片之间由以碳原子为主的链连接。此类单元片的结构大体可以用下图1所示的结构模式来表示。应强调的是，这仅仅是一个虚拟的模式，并不是单元片实际的分子结构。 沥青状组分单元片结构模式示意图石油沥青评价体系目前，在世界范围内具有代表性的道路沥青的评价体系有三种，即针入度分级体系、粘度分级体系和PG分级体系。 针入度分级体系是由针入度、软化点、延度、闪点、溶解度、蜡含量、抗老化等指标构成，是一个相对比较完整的体系；粘度体系主要考虑了沥青的高温性能，主要是由粘度、针入度、老化、延度和闪点组成；PG分级体系是美国联邦公路局研究的成果，是以气候分区确定沥青的使用范围。目前针入度评价体系是我国技术规范中采用的评价体系。由于我国石油应用的行业比较广泛，制定相应标准的部门包括国家标准化管理委员会、生产加工领域的石油化工部门、应用领域的交通部，采用的评价标准也因行业不同、用途不同而有差异。就以70号道路石油沥青技术标准为例，针对三种技术标准进行了比较分析，汇总如下表所示。三种技术标准对比表70号道路石油沥青技术标准项 目 国家标准 (GB/T15180-2010) 中石化1 标准 (Q/SHR 003 - 2000) 交通部标准 * (JTG F40-2004) 针入度（25℃，100g, 5s），1/10mm 60~80 60~80 60~80 针入度指数 PI//-1.5~1.0延度（10℃，5cm/min）,cm 不小于 // 15 延度（15℃，5cm/min）,cm 不小于 100 150100 软化点（环球法），℃ 44~57 46~54 ≮46溶解度（三氯乙烯），% 不小于 99.0 99.5 99.5 闪点，（开口）℃ 不小于 230 230 260 密度（25℃），g/cm3 实测1.00~1.05 实测蜡含量，%（m/m） 不大于 3.0 2.0 2.2 60℃动力粘度，Pa 不小于//160薄膜烘箱试验（163℃，5h） 质量变化，% 不大于 0.8 0.5 0.8 针入度比，% 不小于 55 6861 延度（10℃，5cm/min）,cm不小于 //6 延度（15℃，5cm/min）,cm 不小于 30 100/*：交通部JTG F40-2004中给出的是70号A等级石油沥青的技术要求。从上表分析中可以看出，国家标准综合考虑了全国性的实际情况，对沥青指标的要求总体上相对宽松，如延度指标的试验条件为15℃，而交通部标准中还规定了10℃的延度；软化点、蜡含量、针入度比及溶解度等指标较石化标准和交通部标准也相对较低。对比分析中Q/SHR 003-2000 与JTG F40-2004可以发现，Q/SHR003-2000标准在部分指标上对要高于交通部标准，如15℃延度、蜡含量及质量损失等指标。交通部标准根据道路应用实际情况加强了低温性能的指标要求，新增了10℃延度及60℃动力粘度检测指标，以及针入度指数。关键技术指标1、针入度沥青的针入度与沥青路面的使用性能具有密切的关系，是我国选择沥青标号的最主要依据。针入度表示沥青软硬程度和稠度、抵抗剪切破坏的能力，反映在一定条件下沥青的相对黏度的指标，是指在规定温度条件下，以规定质量的标准针经过规定时间贯入沥青试样的深度，以 0.1mm计，如图所示。针入度测试示意图2、高温稳定性指标高温稳定性是指沥青混合料在高温、慢速荷载作用下抵抗变形的能力，最典型的高温变形就是车辙。车辙的产生是路面破坏的起点，在车辙下凹处如果不能够很好的排除，就容易导致水损害。车辙处积水还是行车的安全隐患，行车舒适性变差。所以车辙等高温稳定性破坏的后果严重，必须加以防止。在抵抗高温变形中，沥青起到重要的作用，SHRP研究表明沥青的性能提供了40%的抗车辙能力，所以准确评价沥青的高温稳定性指标非常的关键。目前，用于表征沥青高温稳定性的指标主要有软化点、粘度。沥青软化点是人为选定的沥青由固态到液态度转变温度的范围中的一个条件粘度，同时也是沥青达到规定条件粘度时的温度。一般来说，沥青软化点越高，沥青的温度稳定性越好。因此，软化点即是反映沥青材料温度稳定性的一项指标，又是沥青粘度的一种量度，我国乃至许多国家均把沥青软化点作为一项重要的性能指标。软化点作为我国道路沥青最常用的三大指标之一，为一般技术人员所熟悉，数值表达也很直观，直接与表示路面发软变形的程度相关联，较高的软化点可以抵抗高温永久变形。粘度是对流体流变特性的一种量度，反映流体发生流动时其内部分子间摩擦阻力的大小。粘度大的沥青在荷载作用下产生较小的剪切变形，弹性恢复性能好，残留的永久性塑性变形小，其抵抗车辙的性能好。60℃粘度指标常作为反映沥青在盛夏季节耐热性的指标。粘度的测试方法比较多，有动力粘度、运动粘度、旋转粘度、标准粘度、恩式粘度等。目前我们采用比较多的是旋转粘度，采用的是布洛克菲尔德黏度计进行测试。旋转粘度是由淹没在沥青试样内转子的阻力力矩和转动的速率计算所得，旋转粘度本质上是剪应力与剪变率的比值，单位Pa• s。旋转粘度测定的是沥青的表观粘度。3、低温性能指标沥青的低温性能也是一个非常重要的指标，因为低温性能直接与路面的功能相关。目前道路沥青的技术规范中，评价低温的指标是延度。脆点在一定程度上也可以表征沥青的低温性能。SHRP研究计划中提出两种评价指标，分别是BBR和DDT。路用沥青的延度是通过在规定的速度和温度下，拉伸标准试件的两端直到断裂的长度，用以表征沥青的延伸性。所谓延性是指受到外力拉伸作用时，所能承受的塑性变形能力，用于衡量沥青的内聚力。沥青的延度与沥青路面的低温抗裂性密切相关。一般而言，沥青延度越大，说明沥青柔性越好，在低温下开裂的风险就越小。沥青延度示意图脆点的实际意义是沥青弹性破坏的界限，作为一种低温抗开裂的指标。通过图4这个沥青形态分布可以看出，软化点到脆点的温度范围是沥青的弹塑性范围，也就是同时兼顾高温和低温性能的范围，所以性能好的沥青软化点要高，脆点要低。粘弹性形态分布图4、温度敏感性指标 沥青的感温性也是一个非常重要的指标，目前用来评价沥青感温性的指标主要有针入度指数PI值，针入度粘度指数PVN和复数模量指数GTS。目前纳入技术规范中的只有针入度指数。针入度指数是由下列公式 计算来的，依据就是针入度的对数与温度之间存在线性关系，A就是直线的斜率。针入度粘度指数是麦克劳德提出的，用25℃的针入度和60℃的粘度计算出来的，见公式3 。对于PI和PVN两个指标哪个更能表征沥青的感温性，不同学者有不同的看法，北美和加拿大的学者们比较认可针入度粘度指数，而我国学者指出针入度粘度指数在表征改性沥青的感温性能上存在弊端，与针入度指数PI值相冲突。 在美国SHRP研究计划中，提出了复数模量指数，就是复数模量的双对数与温度的对数之间存在线性关系，线性关系的斜率就作为复数模量指数，详见公式4。 由于复数模量的测试温度范围是28~76℃，可以表征沥青中温和高温区的感温性。下表给出了三个感温性指标的优缺点，其实将针入度指数和复数模量指数相结合可以有效的评价沥青的感温性，但是由于复数模量的测试采用的仪器弯曲梁流变仪，价格较贵，普及比较困难。三种温度敏感性指标的优缺点PIPVNGTS参数针入度针入度，粘度复数模量温度15℃，25℃，30℃25℃～60℃（或135℃）28℃～76℃试验仪器针入度仪针入度仪和粘度仪动态剪切流变仪试验时间长较短较长优点试验设备普及，容易操作。试验设备较普及，评价温度区间较宽。温度区域很宽，数据采集点的温度差很小，能够反映沥青流变性能随温度的变化趋势。缺点评价温度区域较窄，无法反映整个使用范围内的性能变化，针入度属于条件性指标，计算结果受试验方法精度的影响很大。数据采集点的温度差较大，无法准确反映沥青随温度变化的趋势。试验设备不普及，其准确性和适用性还需要进一步验证，对操作者要求高。5、抗老化指标由于沥青组成的不稳定性，因此抗老化指标也是表征沥青性能的重要指标。目前评价沥青老化性能的方法主要有两种，第一种是自然老化方法，第二种时室内模拟老化的方法。在自然老化方法中，主要有大气老化实验法和路用性能跟踪实验法。大气老化法就是将沥青放在一定的容器中，放在室外固定的位置经受风吹日晒，一定时间后对沥青进行测试；路用沥青跟踪试验法就是将沥青铺建在道路上后，一定时间后从路面中取样，将沥青从石料表明分离出来后进行评价和测试。室内模拟沥青老化的方法主要有两种，一种是短期老化，有薄膜烘箱法（TFOT）和旋转薄膜烘箱法（RTFOT），模拟的是沥青和石料拌合过程中的老化程度，还有一种是长期老化，采用的是压力老化法（PAV），模拟的是在道路上使用10年后的沥青的老化程度。日本和加拿大的沥青联合试验研究对TFOT和RTFOT做出了评价认为TFOT试验的精度虽高，但重现性较低，且对于不同的沥青未必给予同等程度的老化效果。而RTFOT试验则不仅精度高，且重现性也好，尤其是对于不同的沥青能给予同等程度的老化影响。但是众多研究表明，两种试验的结果大体上是相当的，因此许多与沥青有关的标准中注明两种试验方法可以相互替代。目前压力老化容器试验(PAV)已经成为国内外公认的标准长期老化方法，并已经被许多国家推广采用。但压力老化容器试验(PAV)有一定的局限性，它主要考虑到了动态车载、氧、热对沥青性能的影响，并未涉及紫外光与氧的联合作用及水分对沥青性能及组分的影响。6、蜡含量蜡含量是评价沥青性能的一个重要指标，如果沥青中含有较高的腊，高温时，会使沥青变软，导致出现车辙；低温时，容易使沥青变脆，使得沥青路面出现开裂；同时蜡可以降低沥青和石料之间的粘附性，使得沥青和石料发生剥离，此外，沥青中含有蜡的话会使沥青路面的抗滑性能降低，容易出现安全事故。目前蜡含量的测试方法比较多，有裂解法、吸附法、硫化法、色谱法和差示扫描量热法等，目前我国采用的是裂解法。裂解法测试沥青的蜡含量是一个非常复杂的过程，而且影响因素很多、主要过程是先在高温条件下蒸馏，将蜡蒸馏出来，在用无水乙醚和乙醇的混合液溶解后，在低温条件下让腊析出，在通过洗涤将析出蜡纯化，再用石油醚溶解将蜡从漏斗中洗脱下来，再通过蒸发和真空干燥等恒重得到腊的含量。（作者：中华人民共和国泰州海关 才洪美）

随着“十四五”规划的发布，高速公路建设规模将不断扩大，而石油沥青作为高等级道路建设不可或缺的材料之一，需求量也随之步入快速增长的轨道，与此同时，为了提高路面寿命，减少维护费用，国家对公路沥青质量要求将不断提高。为了助力国家交通建设，实现“人享其行、物优其流”的美好愿景，安东帕提供全面的沥青质量控制解决方案，并提供检测设备限时促销活动。限时活动即日起到2022年3月31日，安东帕针对沥青和沥青测试客户推出优惠购买活动。活动期间，只要购买以下三款仪器中的任意一款，将免费获得指定款配件：01自动针/锥入度测试仪PNR 12购买赠送测试杆自动针/锥入度测试仪PNR 12适用于测量高黏性材料如沥青的稠度，定制化的各种配件满足不同标准的测量需求。自动表面检测，无需手动调节样品表面针尖，自动释放测试头传感器连杆可在液面下进行自动对针手动模式下放大镜和LED灯助力样品表面检测测试结果可转换为 NLGI等级、EN沥青值、C值等测试结果可直接导入LIMS系统PNR12选择不同的配件可满足如下标准：ASTM D5、ASTM D217、ASTM D937、ASTM D1321、ASTM D1403、ASTM D7342、ISO 2137、ISO 6873、GB/T 4985、GB/T 269、GB/T 4509。02全自动开口闪点和燃点测试仪CLA 5购买赠送大礼包：软件、杯子一个、点火头一个自动克利夫兰开杯 (COC) 可用于测量和描述样品对热以及对受控条件下测试火焰的响应特性，闪点可测出其与空气形成可燃混合物的趋势，而燃点则可表征其持续燃烧的趋势。适用于润滑剂或沥青材料闪点和燃点测试。可存储 1000 次测试、20 个操作员、100 种样品名称、21 种测试方法统计分析（最小值、最大值、平均值、重复性）测量含硅样品的闪点没有任何问题自动点燃测试火焰，通过电子点火器可将其重新点燃，并且在测试结束时可切断气源对不符合技术规格的结果发出讯息提示Pt100 样品温度探头可通过经用户认证的ASTM 温度计进行动态校准，或通过具有21 个校准点的校正表进行校准标准方法：ASTM D92、ISO 2592、JIS K 2265-4、 AASHTO T48、FTM 791-1103、IP 36、GOST433303弗拉斯脆点测试仪BPA 5购买赠送熔点测试仪BPM 5（熔点是指物质由固态变为液态时的温度，BPM 5可用于测量各种有机结晶物质的熔点）脆点测试仪能够自动测定低温下沥青的脆性。涂有试样的平直薄钢片在规定条件和连续递减的温度下被弯曲，直至沥青涂层出现裂纹为止，沥青涂层出现裂纹时的温度即为沥青的脆点。自动固定和调节涂层测试板无需使用温度计进行冷凝速率调整和温度监测脆点探测系统，无需人工监测数据存储(单机存储 99个数据)，无需传输数据到实验室管理系统，BPA5单机可实现管理测试结束后，无需手动记录结果、测试条件和样品温度EN 12593, JIS K2207, IP 80，GB/T 4510,JTGE20-2011《公路工程沥青及沥青混合料试验规程》中的T0613-1993《沥青脆点试验(弗拉斯法)》熔点测试仪BPM 5安东帕自动针/锥入度测试仪PNR 12、全自动开口闪点和燃点测试仪CLA 5和脆点测试仪BPA 5，安东帕通过这三台代表性仪器为沥青实验室用户提供了一套非常可靠且成熟的测量方案：测量设备通过分析所用的添加剂，帮助您微调沥青产品的弹性。测量结果为评价沥青的长期稳定性以及成分的变形和流动特性提供了依据。您可以联系我们咨询详情或点击下方文字留下您的信息 促销活动 （该活动仅限沥青行业用户）※本活动最终解释权归安东帕公司所有

2017年4月25日，西派特（北京）科技有限公司(以下简称“西派特”）携自主研发的HF-03沥青快速分析仪亮相山西省公路养护技术与管理创新研讨会。本次会议由山西省交通企业协会主办，历时两天，有来自交通运输部科学研究院、公路养护技术国家工程研究中心、交通运输部公路科学研究院交通公路工程研究中心等单位的专家出席此次会议。 HF-03沥青快速分析仪是西派特自主研发的一款高科技产品。该产品通过提取沥青成分中的有效信息、结合化学计量学方法快速同时测定沥青全性质（针入度、软化点、延度、蜡含量、四组分、SBS含量等），可以对沥青的品牌、型号、批次、原产地等信息进行分析和鉴别。 相对于沥青实验室分析，HF-03沥青快速分析仪具有以下明显优势：1. 同时全性质分析；2. 可定性、定量检测；3. 检测速度快；4. 样品用量少；5. 操作简单，无需专业背景；6. 仪器简单便携。 会议期间，西派特参会代表与公路养护技术国家工程研究中心、交通部道路结构与材料重点实验室的各位专家就HF-03沥青快速分析仪采用的快速检测技术进行了深入探讨。HF-03沥青快速分析仪在此次会议中备受关注，并得到在场专家的一致好评。

p 　　 span style=" font-family: 楷体, 楷体_GB2312, SimKai " 在“洛阳铲”、“分金定穴”、“摸金校尉”等荧屏印象之下，大众眼中，考古充满着神秘的色彩，是一个不折不扣的文学类学科。实则不然，考古自诞生以来，就与自然科学及科技手段有着密不可分的关系。改革开放以后，随着考古仪器设备的不断发展和多学科合作观念的深入，中国的科技考古逐步进入快速发展阶段。 /span /p p span style=" font-family: 楷体, 楷体_GB2312, SimKai " 　　在科技考古界分支——硅酸盐质文物研究领域，尤其是古代玻璃研究，有家机构不得不提，那就是上海光学精密机械研究所(以下简称“上海光机所”)。由于上海光机所较早介入该领域且积累了一系列优秀成果，在国内只要从事古代玻璃相关研究工作，就几乎很难避免引用上海光机所的相关成果。而仪器信息网本次采访的主人公——李青会研究员，就是在这里与科技考古结缘。采访中，李青会畅谈了自从事近二十年的科技考古工作，并为我们揭开了它神秘的面纱，包括与科学仪器等科技手段之间的故事。 /span /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 450px height: 253px " src=" https://img1.17img.cn/17img/images/201912/uepic/fd226901-6902-430f-8162-6689c5afa751.jpg" title=" 李老师.jpg" alt=" 李老师.jpg" width=" 450" height=" 253" border=" 0" vspace=" 0" / /p p style=" text-align: center " span style=" color: rgb(0, 176, 240) text-align: center " 上海光学精密机械研究所科技考古中心李青会研究员 /span /p p 　　在内容展开之前，我们首先对李青会的研究领域分支做一个简要介绍。 /p p 　　李青会博士期间师从我国光学材料、非晶态物理学家干福熹院士，目前主要以丝绸之路(草原丝绸之路、绿洲丝绸之路、西南丝绸之路、海上丝绸之路)为主线，利用现代的分析技术(主要采用无损/微损分析技术，基于光学和光谱学技术构建文物的科学表征体系)，研究丝绸之路沿线地区出土的相关文物材料。研究文物材料主要聚焦在无机材料中的古代硅酸盐材料(如玻璃、陶瓷、玉器、硅酸盐类颜料等)。研究内容是在系统整理古代玻璃、古代玉器等出土文物的历史文化背景材料基础上，与国外同时期或相近时期同类文物进行比较研究，将古代硅酸盐质文物的材料属性、加工工艺、产地和溯源研究、病害特征等物质属性研究与文物的社会属性研究有机结合，以求对古代社会生活、经济发展，以及相关的国内各地区间及中、外文化、技术交流有深入认识。 /p h1 label=" 标题居中" style=" font-size: 32px font-weight: bold border-bottom: 2px solid rgb(204, 204, 204) padding: 0px 4px 0px 0px text-align: center margin: 0px 0px 20px " span style=" font-size: 18px color: rgb(255, 0, 0) " strong span label=" 明显强调" style=" font-size: 18px font-style: italic font-weight: bold line-height: 18px " 结缘近20年：与科技考古的故事 /span /strong /span /h1 p 　　 strong 学科前序：干福熹院士与古代玻璃科技考古 /strong /p p 　　20世纪50年代，干福熹院士最初加入中科院时，从事的是两大学科的研究：理学下的光学和凝聚态物理、工学下的材料科学与材料物理化学。 /p p 　　1959年，干福熹在苏联考察期间，与苏联著名古代玻璃科学家Besbrodov教授交流，Besbrodov教授曾问干福熹，“人们都在讲中国古代玻璃是公元6-7世纪从西方传入的，中国发明瓷器很早，为什么不会制造玻璃?” 干福熹当时对中国古代玻璃一无所知。但回国参观中国历史博物馆时，看到了战国时代的蓝色“琉璃”，干福熹便产生了一个想法，如果这是玻璃，那么中国古代玻璃产生的时间就更早了。从此，干福熹对中国古代玻璃产生兴趣并密切关注。此后，他在1964年和1979年先后两次拜访剑桥大学Joseph Needham教授，并获得中国洛阳金村古墓的玻璃成分与西方古代玻璃完全不同的信息。这更激发了干福熹对中国古代玻璃研究的兴趣，于是其研究领域进一步跨入了科技考古学中。 /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 450px height: 299px " src=" https://img1.17img.cn/17img/images/201912/uepic/40dbc5aa-0306-4062-a11d-8d791e952513.jpg" title=" 2012会议.jpg" alt=" 2012会议.jpg" width=" 450" height=" 299" border=" 0" vspace=" 0" / /p p style=" text-align: center " span style=" color: rgb(0, 176, 240) " 2012国际古代玻璃学术研讨会 /span /p p 　　干福熹认为，科技考古的目的是保护历史文物和进行文明探源。在后来的学术研究中，干福熹成果丰硕,并多次主持了关于古代玻璃研究的国际研讨会，为中国古代玻璃研究作出了重要的贡献。 /p p 　　2002年，师从干福熹院士的李青会完成了博士学位，并开始协助干福熹进一步开展古代玻璃研究。由此缘起，李青会开启了他科技考古近20年的研究工作。 /p p 　 strong 　缘起缘续：与科技考古这20年 /strong /p p 　　2002年，李青会师从干福熹院士完成博士学位后，开始迈入科技考古领域，这近20年的科技考古研究工作历程，大致可以用两个转变来概括，即从兼职到全职 从以化学成分特征分析等简单自然科学手段解决科技考古问题，到将文物历史背景、着色工艺、制作工艺等文物学、历史学与自然科学相融合方式来解决科技考古问题。 /p p 　　2002年开始，李青会由于人手不足，同时还要进行存储材料相关技术研究，古代玻璃相关的科技考古研究工作只能作为副业兼着做。到2004年前后，随着干福熹院士主导举办的一系列古代玻璃相关学术会议与论坛的开展，历史领域、科学技术领域、考古学领域等交叉领域专家开始不断交流与合作。此时，上海光机所与国内考古研究所、博物馆等相关文博单位也逐渐建立起联系，并开展了一系列合作。这样，科研机构与文博单位从两个相互独立的学科单位，经过合作研究中的不断磨合，互相关注各自需求，逐渐形成了合作共享的良好关系。经过一段时间的积累，上海光机所目前已经与国内大部分文博单位进行了合作。 /p p 　　2007年，李青会前往东京理科大学访学，同时参与两个课题方向，一是仪器开发(下一代扫描电镜系统、TES能谱仪等的开发及应用)，二是科技考古。在之前五年科技考古研究经验与考古学家的合作积累下，李青会感到新的研究方向更加得心应手。随着科技考古研究的逐渐深入，李青会也逐渐认识到，他所从事的古代玻璃研究，若仅仅做化学成分特征研究，只是纯粹的数据获取，并不能更好的解决考古问题。于是，基于古代玻璃特色及与现代玻璃的区别，他将着色工艺、制作工艺等也逐渐列入到研究内容中，希望能更好的协助科技考古研究。 /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 450px height: 299px " src=" https://img1.17img.cn/17img/images/201912/uepic/01d7ce8d-f667-41a1-954e-1d33a9aa92be.jpg" title=" 玻璃珠.jpg" alt=" 玻璃珠.jpg" width=" 450" height=" 299" border=" 0" vspace=" 0" / /p p style=" text-align: center " span style=" color: rgb(0, 176, 240) " 随州擂鼓墩M1(曾侯乙墓)出土的战国早期玻璃珠 /span /p p 　　2009年，李青会回国。此时，随着团队与科研力量的加强，他便逐渐专职开展科技考古工作，并在研究过程中认识到，在利用仪器检测手段获取广泛数据基础上，还需进一步解决考古学术问题，使得科技考古研究更加知其所以然、有据可依。比如对出土器物进行研究，要结合考古学对墓葬的背景材料或其他相关器物的认识，把古代玻璃研究得出的结论与考古学得出的结论进行比对才可以，这样就相当于利用成分分析等科技手段获得的补充数据去解决考古学的问题。 /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 600px height: 202px " src=" https://img1.17img.cn/17img/images/201912/uepic/c7a211f4-ecb2-4018-a6f7-c7642ce35bf1.jpg" title=" 玻璃珠研究.jpg" alt=" 玻璃珠研究.jpg" width=" 600" height=" 202" border=" 0" vspace=" 0" / /p p style=" text-align: center " 　　 span style=" color: rgb(0, 176, 240) " 著名的“蜻蜓眼玻璃珠”拉曼光谱现场测试照片 /span /p p style=" text-align: center " span style=" color: rgb(127, 127, 127) " ( /span span style=" color: rgb(127, 127, 127) " 有文献记载“遂候以要做珠”，大家普遍认为曾侯用的这个“珠”可能是国产玻璃。但李青会团队通过结合这批玻璃器皿的乳浊、着色特征还有成分体系(利用拉曼光谱)，证明这批玻璃珠由西方输入，而且很可能就在地中海东岸地区生产) /span /p h1 label=" 标题居中" style=" font-size: 32px font-weight: bold border-bottom: 2px solid rgb(204, 204, 204) padding: 0px 4px 0px 0px text-align: center margin: 0px 0px 20px " span style=" font-style: italic font-weight: bold line-height: 18px font-size: 18px color: rgb(255, 0, 0) " 神秘科技考古背后：多学科交叉与融合 /span /h1 p 　　干福熹院士曾表示，科技考古要人文科学与自然科学相结合，要做无损分析，要不断改进研究方法，中国考古的成果要拿到世界的环境下对比。正如所言，科技考古的多学科融合，在上海光几所科技考古中心不仅体现在自然科学与历史学、文物学等人文科学的融合，也体现在团队人才培养的“文理全才”。 /p p 　 strong 　科技考古的升级——多学科融合 /strong /p p 　　据了解，上海光机所科技考古中心采用的自然科学与考古学、历史学领域的文理交叉融合研究的方法，在国内是比较成功的，也是比较先进的。学科融合不仅体现在学术上的相互借鉴，更体现在科技考古工作中与考古学家或历史学家的交流。通过彼此的借鉴与交流，科技考古便从单纯的数据获取为主，升级到满足自然科学与人文科学双方的需求，从而实现真正的学科融合。 /p p 　　李青会表示，“我们是用现代科学技术分析古代材料，实际上从学科角度来说，它就是一个材料学的一个研究思路和一个科学分析仪器方法选择的问题。而解决完材料学研究思路与仪器选择后，融合人文科学进一步研究，才能让自然科学获得的数据在科技考古中获得真正意义。“ /p p 　　学科的融合对科技考古意义重大，比如分析器具的来源问题，就需要对器具的器形纹饰特征和科技的结论结合起来。法门寺地宫里面有一套玻璃茶托和茶盏，在当时没有科技考古检测情况下，由于唐代盛行喝茶，有瓷器，所以大家认为这两种玻璃是国产的。但李青会团队对样品检测后，发现这两种玻璃都是从西方输入的伊斯兰玻璃，并不是国产的。 /p p 　　 strong 多元融合下的特殊需求——“文理全才” /strong /p p 　　上海光机所之所以较短时间内在科技考古领域取得不错的成绩，除了光机所在仪器开发应用方面的优势，在人才培养方面重视“文理全才”也是一个重要因素。 /p p 　　据介绍，科技考古团队的研究生都是理工类出身，他们在仪器应用方面就具有了一定优势。同时，科技考古研究组与其他小组还有一个很大的不同，就是内部主导的科研数据都是研究人员自己获取，而不是交给测试员。另外，研究人员基本上都要接触文物，所以无论之前是学光学的还是学材料或分析的，每个人最终都要补上考古历史的知识，与检测样品相关的考古历史学背景知识都要增强。这就相当于团队中每个人都需要走完样品检测、样品历史背景资料了解，检测和数据的解析等全部流程，需要从头到尾参与，而不是每人只负责其中的某个流程，这就要求研究人员必须成为科技考古的“文理全才”。 /p h1 label=" 标题居中" style=" font-size: 32px font-weight: bold border-bottom: 2px solid rgb(204, 204, 204) padding: 0px 4px 0px 0px text-align: center margin: 0px 0px 20px " span style=" font-size: 18px color: rgb(255, 0, 0) " strong span label=" 明显强调" style=" font-size: 18px font-style: italic font-weight: bold line-height: 18px " 科技考古与科学仪器那些事 /span /strong /span /h1 p 　 strong 　科技考古实验室的仪器“很忙” /strong /p p 　　李青会表示，科学仪器对于科技考古十分重要，是获取数据信息的主要工具。“除了节假日，我们的仪器基本是保持开机状态的，使用十分频繁。对于我们来说，古代玻璃研究的每一项检测都需要信息，如果某个仪器一周不能工作，相当于我们研究的许多数据获取就停滞了。所以，实验室的仪器基本上一年都在工作状态中。” /p p 　　 strong 科技考古都用哪些仪器?与其他领域有啥不一样? /strong /p p 　　由于科技考古的样品对象比较特殊，比如相对完整的文物或者级别比较高的文物，这样的样品不能随意损坏或丢弃，所以我们对仪器技术就有了一定的要求，尤其越珍贵的文物样品，我们所选择的仪器检测技术局限性就越大。上海光机所科技考古中心经过经过多年的系统调研和实践应用，最终总结出来光学和光谱分析技术(包括需要取样、无损的，或只需要少量，比如激光剥蚀等)是比较适合的检测技术。 /p p 　　李青会表示，“我们实验室应用最广泛的仪器，主要是化学成分分析类的，因为无论是无机质文物、金属还是非金属，要测合金比例或玉石的元素组成等都涉及到成分分析。对于古代玻璃无机材料，最普遍的还是能量色散型X射线荧光光谱仪，因为这种仪器即可以是大型的，也可以是便携的，比较实用。” /p p 　　上海光机所利用自身在光学仪器研发方面的优势，逐渐将一系列以往在材料科学领域的科学仪器检测方法系统地引入到科技考古行业中，并从基础研究到推广应用都做了大量工作，比如推动激光拉曼技术、光学相干断层扫描(OCT)技术等的大面积应用和组合使用。 /p p 　　那么，科技考古的科学仪器应用与其他领域有什么不同呢? /p p 　　首先看看检测流程。检测流程往往影响最终的获取信息，比如陶瓷做热释光，由于外界辐射对其影响较大，检测流程就需要先做热释光，再做X射线荧光成分分析，顺序颠倒就会对后期释光剂量有影响。 /p p 　　定量标准也不同。由于文物样品特殊性，许多材料需要针对不同物质做相应定量标准，这就涉及到基础标准物质的研发，或者是校准方法的制作。因为只有统一的标准参考样品，才能和别人的数据共享。另外，仪器中若没有古代颜料等样品对应的数据库选择，还需要去做数据库图谱管理工作。 /p p 　　 strong 科技考古仪器选购、应用二三事 /strong /p p 　　所谓科技考古仪器的选购，就是根据考古科技的实际需求，选择现有的或进行一定改进的仪器设备，并在实践应用中摸索出合理的技术方法的组合。李青会认为，“选择适合的仪器方案，并不是越高端越好。为了减少国家科技资源浪费，我们在购买仪器设备之前，至少在已经配置相关产品的三家以上单位，拿样品去做测试评估。” /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 450px height: 253px " src=" https://img1.17img.cn/17img/images/201912/uepic/814c2af5-5365-4c33-915c-17509669dc09.jpg" title=" 李老师研究.jpg" alt=" 李老师研究.jpg" width=" 450" height=" 253" border=" 0" vspace=" 0" / /p p style=" text-align: center " span style=" color: rgb(0, 176, 240) " 李青会老师与XploRA& #8482 /span /p p 　　比如拉曼光谱仪(XploRA)的引进，在引进前，相关文物材料的结构分析是由粉末X射线衍射仪(XRD)承担的。虽然XRD分辨率很高，但对粉末样品百分含量有要求，比如5%或以下就探测不出来，这对文物检测是很不方便的。而且XRD对于大尺寸样品也受样品槽的限制。而显微拉曼光谱技术则有微区分析、灵敏度高、无损等优势，可分析小量样品，甚至是微量样品，这对考古类珍贵样品分析来说是至关重要的。 /p p 　　在仪器附加功能的选配方面，也需要根据需求选配。李青会讲到“还以XploRA为例，起初实验室使用的是其反射照明模式观察和定位样品，在与HORIBA产品人员的一次交流中，了解到了XploRA的透射照明模式，在增加了该透射功能后，对于半透明和透明的样品，如宝石内部的包裹体特征就很容易观察清楚，从而可以方便地对样品内部细节进行表征。而XploRA的另外一个特色——针孔共聚焦功能，可以获取亚微米级别的空间分辨率，对于不能破损、透明或半透明的样品，激光能穿透到特定样品深度，获取该深度的样品信息，实现样品内外层组成物相的差异分析，特别是对需要分析分层范围、分层厚度在仪器共焦范围(亚微米)之内的时候，这个功能十分管用。” /p h1 label=" 标题居中" style=" font-size: 32px font-weight: bold border-bottom: 2px solid rgb(204, 204, 204) padding: 0px 4px 0px 0px text-align: center margin: 0px 0px 20px " span style=" font-style: italic font-weight: bold line-height: 18px font-size: 18px color: rgb(255, 0, 0) " 关于中国科技考古发展 /span /h1 p 　　 strong 中国科技考古现状：蓬勃发展 /strong /p p 　　李青会表示，党的十八大以来，习近平总书记高度重视文化自信这一更基本、更深沉、更持久的力量，并多次就传承中华优秀文化发表重要讲话，而文物又是历史文化信息的一个重要载体。在国家高度重视下，我国有越来越多的高校开设了科学技术史、文化遗产，或文化遗产保护等相关学科，去年就增加约六七十所，比如浙江大学、复旦大学、上海交通大学等。 /p p 　　相关人才得到培养的同时，国家还在省一级博物馆、考古所等投入大量资金，大大提高了科研设备硬件水平，如许多综合类的科研设备都达到了千万元级别。从硬件条件方面，我国已经赶上甚至超过国外水平，包括相关高校院所相关文物研究设备条件在国际上都是不弱的。 /p p 　　这些都说明我国科技考古正处于蓬勃发展的时期。 /p p 　 strong 　我国科技考古发展的一些建议 /strong /p p 　　虽然我国科技考古呈现繁荣发展景象，但也存在一些不足。李青会也就此谈了一些看法和建议。 /p p 　　人才缺乏导致仪器利用率低。由于文物单位相关工作人员，有的是文科背景出身，有的是仪器等理工背景出身，这就需要把他们培养成即懂文物本身，又懂仪器等科技方法的综合人才，这是比较难的，国内整体上也比较缺乏此类人才，这也直接导致了科学仪器利用率不高，造成一定资源闲置浪费等问题。而提高一系列供应效率，集中人员、技术、仪器装备等力量共享利用就是一个很有效的方案。欧美在这方面做的就比较好，集中人才、仪器设备等各方力量开展研究，在一些重要的文化遗产保护或科技考古研究中就发挥了重要作用。 /p p style=" text-align: center" img style=" max-width: 100% max-height: 100% width: 450px height: 253px " src=" https://img1.17img.cn/17img/images/201912/uepic/ab0c8388-1884-4ef5-a9b4-0e4c87121c16.jpg" title=" 实验室介绍.jpg" alt=" 实验室介绍.jpg" width=" 450" height=" 253" border=" 0" vspace=" 0" / /p p style=" text-align: center " span style=" color: rgb(0, 176, 240) " 李青会老师介绍实验室 /span /p p 　　文物监管比较严。我国的现状是，往往文物越珍贵，监管的就越严。在文化遗产对社会资源敞开研究程度角度讲，我国与国外还有差距。虽然我们也在开放方面采取一些措施，但总体来讲，在资源公众开放利用，加强其价值方面，我们还是比国际发展的步调要缓慢，在此方面，我国还要做更多努力。 /p p br/ /p

石油中胶质和沥青质怎样检测??从煤油馏分中开始，随馏分沸点的升高，其含量不断增加，渣油中含量大，沥青质全部集中在渣油中。怎么检测出具体数据，山东盛泰仪器厂家家推出的SH8019实际胶质测定仪是专门用于测定航空汽油和车用汽油中实际胶质含量的仪器。适用于按GB/T 8019-2008《燃料胶质含量的测定喷射蒸发法》等效ASTM D381中规定的方法，对航空汽油和车用汽油进行实际胶质试验，配备专用的无油静音空压机。 [object Object]石化油品检测仪器系列全自动开口闪点仪全自动闭口闪点仪微量水分仪运动粘度仪破抗乳化仪自动酸值酸度仪全自动凝点倾点仪自动脱气震荡仪泡沫测定仪锈蚀腐蚀仪铜片腐蚀仪石油密度仪全自动水溶性酸碱仪气相色谱仪耐压测试仪油介损电阻率测试仪闪点仪运动粘度仪凝点倾点仪破抗乳化仪泡沫测定仪润滑油脂水分仪酸值仪锥入度仪滴点仪宽温滴点仪润滑脂相似粘度仪润滑油蒸发损失度仪润滑油氧化安定性仪（旋转氧弹）润滑油脂蒸发损失度仪润滑脂油铜片腐蚀仪抗水淋性仪空气释放值仪全自动四球机开口闪点仪闭口闪点仪量热仪定硫仪全自动酸值酸度仪全自动微量水分仪全自动冷滤点测定仪全自动凝点倾点仪饱和蒸汽压测定仪馏程测定仪沸程测定仪馏分燃料油氧化安定性仪实际胶质测定仪铜片腐蚀仪石油密度仪全自动汽油氧化安定性仪石油残炭测定仪机械杂质度仪十六烷值辛烷值仪石油色度仪硫含量测定仪石油产品苯胺点测定仪机械杂质度仪防冻液冷却液冰点仪全自动表观粘度仪发动机油泵送温度测定仪滚筒安定性试验仪油污颗粒度仪梯姆肯试验机十万次剪切试验机液压油热稳定性测定仪液压油过滤性测定仪液压油水解安定性试验仪绝缘油带电倾向性测定仪有机热载体氧化安定性测定仪内燃机油成焦倾向性测定仪全自动自燃点仪化学发光定氮仪石油产品硫醇硫测定仪体积电阻率测定仪润滑脂漏失量测定仪润滑油脂机械杂质度仪润滑脂合成橡胶试验仪全自动沸程仪盐雾腐蚀试验器石油产品灰分仪液体石油产品烃类测定仪润滑脂压力分油器润滑脂钢网分油器润滑脂粘附性测定仪润滑油脂防冻液仪器清单明细化学发光定氮仪SH0248C全自动凝点冷滤点仪SH128 全自动防冻液冷却液冰点仪SH0048B 全自动相似粘度仪全自动苯胺点测定仪SD262B全自动结晶点测定仪低温闭口闪点仪SRH12润滑油抗磨试验机减压馏程测定仪SD0165石油产品流程测定仪原油6孔水分仪康氏残碳测定仪油品烟点测定仪sd382高低温锥入度仪SD2801E喷气燃料银片腐蚀测定仪SH0023发动机冷却液腐蚀测定仪SH0085发动机冷却液沸点测定仪SH0089全自动机械杂志仪SH101B石油产品密度测定仪SH102A自动表面张力仪SH107自动酸值测定仪SH108B表面粘度测定仪SH110发动机冷却液泡沫倾向性测定仪SH126C润滑油高温泡沫测定仪SH126E润滑脂滚筒性测定仪SH129辛烷值和十六烷值测定仪SH131馏分燃料油氧化安定性测定仪SH0175自动选装氧化安定性测定仪SH0193C变压器油氧化安定性SH0206凝点倾点冷滤点测定仪SH0248自动碱值测定仪SH251石油产品酸值酸度测定仪SH258全自动水溶性酸碱测试仪SH259B润滑脂手动捣脂器SH269-1便携式油污颗粒计数器SH302A全自动油污颗粒计数器SH302B石油产品密封适应性指数仪SH305润滑脂氧化安定性SH325深色石油硫含量测定仪SH387石油产品硫氯测定仪SH409高温剪切测定仪SH417防锈油脂湿热试验箱SH601自动溴价溴值测定仪SH630发动机冷冻也与制冷剂相容性SH0669紫外荧光定硫仪SH706B 自动抗燃油自燃点测定仪固体自热实验仪石蜡熔点测定仪石油蜡含量测定仪液化石油蒸汽压测定仪原油蜡含量测定仪自动石油产品蒸气压测定仪石油产品蒸气压测定仪工业芳烃铜片腐蚀仪梯姆肯磨损试验仪石油产品酸值酸度试验仪润滑脂蒸发度仪发动机胶质测定仪抗水喷雾试验仪润滑脂防腐性测定仪全自动沸程仪沸程仪sd260b 双联石油水分仪SH607内燃机油成焦倾向性测定仪SH8018 汽油氧化安定性sd8022 齿轮油抗乳化仪SH107B 自动表面张力仪SH0209液压器油氧化安定性SH0325 B全自动润滑脂氧化安定SH606防锈油脂湿热试验箱SH706b自动自然点测定仪SH706c固体自然点测定仪全自动奥氏运动粘度仪平衡法低温闭口闪点仪SHD385B绝缘油带电度全自动测定仪

2020第二届重载沥青与桥面铺装技术大会于8月27-28日在山西太原召开，本届大会以“更好的桥面铺装，更耐久的桥梁”为主题，共设置三个分论坛、十三场主题报告、两场圆桌讨论和两场参观观摩，共同探讨国内外桥面铺装现状、桥面铺装的结构形式、桥面铺装设计标准与方法、桥面施工工艺及装备、复合浇注式沥青混凝土铺装、环氧沥青铺装、超高性能混凝土UHPC铺装、桥面防水防腐材料、智能管养与检测技术、其它桥面铺装新技术、新材料、新工艺、新装备等。 上海昌吉地质仪器有限公司携多款新型浇筑式沥青检测设备精彩亮相展会。展会上公司生产的新型浇筑式沥青检测设备吸引了大批专业人士的驻足、咨询与交流。 本次展会，上海昌吉展出的多款新型浇筑式沥青检测设备，其中本公司专门研发的新品SYD-0768 浇筑式沥青混合料贯入度试验仪吸引了大批专业客户的目光，收获广大好评，咱们一起看看吧！SYD-0768浇筑式沥青混合料贯入度试验仪 主要用于测量浇筑式沥青混合料的贯入度，即在指定的温度和荷载作用下，沥青混合料的变形量，从而评价浇筑式沥青混合料的高温稳定性，并指导其配比设计。 下列两款仪器，动稳定度和破坏应变也是浇筑式沥青必须检测指标，仪器名称：SYD-0719C-2自动车辙试验仪和SYD-0730A 多功能全自动沥青压力试验仪。想了解设备详细资料的用户可给小编留言，或关注上海昌吉公众号，联系我们公众号客服。SYD-0719C-2 自动车辙试验仪（三轮科研）SYD-0730A 多功能全自动沥青压力试验仪 本次展会，上海昌吉推出多款浇筑式沥青检测新产品，向来自全国各地的客户多角度、深层次地展示产品与服务。好的产品少不了客户的检验，欢迎新老客户对咱们上海昌吉新产品提出改进意见。立足客户需求，完善产品与服务，上海昌吉地质仪器有限公司始终如一！

从镇江检验检疫局传来消息，由该局主持研究的《煤沥青微量元素测定方法 电感偶合等离子体-原子发射光谱法》由国家质检总局正式发布，作为国家行业标准于2010年7月16日正式实施。 　　该标准适用于煤沥青、石油焦及煅后石油焦中钙、铁、钠、镍、硅、钛、钒的测定，具有一次性检测多种元素的优点，测定煤沥青中镍、硅、铁、钙、磷、钠、钒、钛等金属元素含量，克服原来使用化学方法中逐一检测元素含量的缺点。同时具有排除元素之间的干扰、法简单高效，具有较高的准确性和精密度，可满足产品质量控制的需要。 　　煤沥青是我国向美国、俄罗斯、澳大利亚、欧洲等国家出口的重要产品之一。镇江检验检疫局科研工作小组人员从2005年就开始研研究实践，先后完成了情况调研、标准查新、规程编制规划、规程草案编写、规程草案讨论、征求意见、规程草案修订、形成规程送审稿、审定、报批等各个阶段的工作。该标准的正式实施将对炼铝企业发展提供技术保障。

一、沥青软化点测定仪的原理沥青软化点测定仪是一种通过试验测定沥青在特定条件下的软化点的设备。在道路桥梁、建筑等领域，沥青作为一种重要的建筑材料，其性能指标对工程质量有着至关重要的影响。而沥青软化点是评价沥青性能的重要指标之一，因此，沥青软化点测定仪在这些领域的应用具有重要意义。二、沥青软化点测定仪在道路桥梁工程中的应用在道路桥梁工程中，沥青作为一种主要的铺装材料，其性能对道路桥梁的质量和寿命有着重要影响。沥青软化点测定仪的应用可以有效地控制沥青的性能指标，从而提高道路桥梁的耐久性和使用寿命。例如，在高速公路的路面施工中，沥青的铺设需要具有高耐久性和抗滑性能。为了确保沥青的性能符合要求，施工单位可以使用沥青软化点测定仪进行检测，从而保证沥青的质量和铺设效果。三、沥青软化点测定仪在建筑工程中的应用在建筑工程中，沥青作为一种重要的防水材料，其性能对建筑物的防水效果和使用寿命有着重要影响。沥青软化点测定仪的应用可以有效地控制沥青的性能指标，从而提高建筑物的防水效果和使用寿命。例如，在建筑物的屋顶防水施工中，沥青的铺设需要具有优良的防水性能和耐久性。为了确保沥青的性能符合要求，施工单位可以使用沥青软化点测定仪进行检测，从而保证沥青的质量和铺设效果。

安东帕为沥青、柏油行业及应用量身定制高质量的解决方案。安东帕提供多种产品线的综合解决方案，ProveTec系列产品在石油石化分析领域有多年经验，拥有软化点测试仪、弗拉斯脆点测试仪、数字延度仪等产品，结合密度计、旋转流变仪等多达9种仪器，为您提供测量21种参数的可能并符合36项标准，测量柏油组成和成分的粘度、形变和流动特性、后续跟踪分析的消解柏油样品、软化点、渗透力、延展性、拉伸性能、脆点等。 2017年，安东帕隆重推出全新的SmartPave 92动态剪切流变仪。SmartPave 92可以满足实验室对于沥青结合料以及混合料的检测和质控的需要。如同SmartPave 102，这一新产品基于安东帕成功的模块化智能流变仪技术，确保您获得最精确和最稳定的测量结果。 SmartPave 92采用帕尔贴温控系统对沥青样品进行精确的温度控制，从而可以按照各种行业标准进行结合料和混合料的测试，符合的标准包括AASHTO T315, AASHTO T350, AASHTO TP101, ASTM D7175, ASTM D7405, DIN EN16659，和DIN EN14770。 同时，SmartPave92流变仪可以使用同心圆筒帕尔帖温控测量系统，替代旋转粘度计，进行符合AASHTO T316, ASTM D4402 和 DIN EN13302标准的黏度测试。 SmartPave 92 的优势1.RheoCompass软件提供功能强大，又易于上手的测试模板，手把手协助您展开对于沥青的测试2. 独特的环形TruRay光源让您更清楚的观测样品和测量区域，确保正确的样品填充量3. 使用快速连接器，单手即可方便快捷地安装或更换测试夹具，无需使用额外的工具4. ToolmasterTM自动识别功能，快速自动识别测量夹具和温控系统的型号并设置参数

热烈祝贺上海衡平仪器仪表厂于2016上半年成功发布*--DV-1C：粘度计 旋转粘度计 沥青*粘度计产品特点全新*LCD显示屏，操作简单方便，屏蔽性能*显示信息：粘度（mPa.S, Pa.S）%扭矩转速/转子剪切速率/剪切应力量程符合*标准中华人民共和国交通行业标准JTJ052《公路工程沥青及沥青混合料试验规程》中的T0625《沥青布氏旋转粘度试验（布洛克菲尔德粘度计法）》可选配电脑连接口及粘度上位机软件：选配RS-232通讯接口连接电脑选配粘度上位机软件可实现数据采集和数据分析,全程监控粘度-温度曲线其他可选配配件：加热炉：使用温度＜250℃外循环式20ml小量样品适配器：使用温度＜120℃粘度计*恒温水浴产品介绍：DV-1型布氏旋转粘度计，是按照中华人民共和国交通行业标准JTJ052《公路工程沥青及沥青混合料试验规程》中的T0625《沥青布氏旋转粘度试验（布洛克菲尔德粘度计法）》规定的要求*制造的，主要用于按布洛克菲尔德粘度计旋转法测定道路沥青在45℃以上200℃以下温度范围内的表观粘度。根据粘度-温度曲线还可用来确定沥青混合料的施工温度。DV系列沥青*旋转粘度计测量数值数据表图实时显示测试记录*参数型号DV系列沥青*机测量范围1~2× 105mPa.S转子规格标配21、27、28、29号转子转子转速（转/分）5、10、20、50PC接口选配打印机接口√ 测量精度± 1%（牛顿液体）供电电源交流110~240VAC 50/ 60HZ工作环境5℃ ~35℃ ，相对湿度不大于80%外形尺寸380mm× 320mm× 390mm净重4.5kg标配21、27、28、29号转子图与小量样品适配器配套图

研究背景铁尾矿是铁矿石经破碎、筛分、研磨、分级、浮选等工艺流程，筛选出铁元素后的剩余产物，其主要成分与公路工程用集料相同。但现阶段我国的铁尾矿综合利用率较低，主要采取堆存方式进行处置，该做法造成了资源的浪费。公路工程建设过程中需要大量的筑路材料，若能将铁尾矿用作筑路材料，即可以降低公路工程造价，也可减少其对环境的污染。本文以表面自由能理论为依据,采用座滴法测量铁尾矿和不同沥青的表面能参数,并计算沥青与不同集料间的粘附功,以衡量铁尾矿与沥青间的粘附性能。实验方法与仪器1.表面能测试本文使用蒸馏水、甘油以及甲酰胺作为测定接触角的试剂，后测定这三种试剂在试样表面的接触角，并计算沥青与集料的表面能及其分量。本文采用德国KRÜ SS公司的DSA100接触角测量仪在25℃下对四种集料和沥青的接触角进行测试。DSA100接触角测试仪2.原材料本文研究过程中采用东海70号沥青、SBS改性沥青（I-D）和SBR改性乳化沥青蒸发残留物三种沥青，集料采用石灰岩、玄武岩和铁尾矿石。原材料各项技术均能满足现行技术规范要求，其中沥青技术指标如表1所示，四种集料矿物成分如表2所示。表1 沥青技术指标表2 矿物成分组成表结果与讨论1.接触角图1 接触角测试结果由图1实验结果可以发现，四种集料与测试液体的接触角差别较小，且不同材料与各测试液体的接触角试验的重复性较高。其主要原因可能是，各集料在测试前均对其表面进行了分割和磨平，这使得其空隙情况差别不大，因此各接触角差别不是很大。整体而言，蒸馏水与集料间的接触角随SiO2含量的增加而减小，其主要原因是水为极性分子，SiO2对水的极性能力较大，二者接触时更倾向于吸附更多的水以平衡表面力场，降低表面能，所以表现出水与集料间的接触角随SiO2含量的增加而减小的现象。SBS改性沥青与水和甘油间的接触角最大，SBR改性乳化沥青蒸发残留物与水间的接触角次之，基质沥青最小；SBR改性乳化沥青蒸发残留物与甲酰胺间的接触角最大，SBS改性沥青次之，基质沥青最小。图2γL与γLcosθ的关系为进一步验证测试结果的准确性，将不同测试液体的表面能γL与γLCOSθ进行线性拟合，结果如图2。由图 2可以发现，测试液体的表面能γL与γLCOSθ 线性拟合后的相关系数（R2）均大于0.90。表明二者之间具有良好的线性关系，即测试结果可靠。2.表面自由能图3表面能计算结果分别综合3种测试液体的表面能参数及其在集料和沥青的接触角计算集料和沥青的表面能及其分量，计算结果如图3所示。由图3(a)-(c)可以看出，四种集料的表面能相差不大，其中石灰岩的表面能最大，铁尾矿1的表面能最小，该现象的主要原因是石灰岩中的SiO2含量最小，铁尾矿1中SiO2含量最大，已有研究结果表明集料的表面能与SiO2含量呈负相关关系。四种集料中，铁尾矿2的极性分量最大，色散分量最小，石灰岩的极性分量最小，色散分量最大。由(d)-(f)三种沥青的表面能存在较大的差异，其中SBS改性沥青的表面能最大，SBR改性乳化沥青蒸发残留物的表面能最小，其可能原因是改性乳化沥青制备过程中需要加入乳化剂，乳化剂的作用原理是降低沥青与水间的界面能，提高二者间的稳定性，蒸发残留物制备过程中的乳化剂未能完全蒸发，导致其表面能的降低。SBS改性沥青的极性分量最小，色散分量最大，SBR改性乳化沥青的极性分量最大，色散分量最小，其可能原因是SBS蒸发残留物中的乳化剂未能充分挥发，使得其蒸发残留物的极性增强。3.粘附功的计算图4不同沥青与集料间的粘附功通过沥青和集料的表面能数据计算得到二者间的粘附功，计算结果如图4。由图4可以发现，不同沥青与不同集料间的粘附功存在一定差别，其中SBS改性沥青与石灰岩间的粘附功最大，为71.16mJ/m2，而SBR改性乳化沥青蒸发残留物和铁尾矿1之间的粘附功最小，为66.24mJ/m2。整体而言，石灰岩与各沥青间的粘附功要大于玄武岩和铁尾矿，该现象产生的原因是石灰岩的SiO2含量仅为0.76%，其碱性要强于玄武岩和铁尾矿。SBS改性沥青与集料间的粘附功要大于70号基质沥青和SBR改性乳化沥青蒸发残留物，究其原因，SBS改性剂的加入使得沥青的极性降低，而SBR改性乳化沥青蒸发残留物中乳化剂在挥发不完全情况下，其极性更大，且残留物制备过程中需要经过高温蒸发，使得沥青发生了一定程度的老化，老化后的沥青极性增强。小结石灰岩的表面能最大，铁尾矿的表面能小于石灰岩和玄武岩，且铁尾矿的极性分量大于石灰岩和玄武岩，色散分量小于二者。不同沥青与不同集料间的粘附功存在一定差别，SBS改性沥青与集料间的粘附功大于基质沥青和SBR改性乳化沥青蒸发残留物，石灰岩与沥青间的粘附功要大于玄武岩和铁尾矿。参考文献：[1]王鑫洋,苏纪壮,祁冰.基于表面能理论和拉拔试验的铁尾矿与沥青黏附性研究[J/OL].武汉理工大学学报(交通科学与工程版):1-11[2022-12-15].

锥入度测定仪仪器维护、注意事项A3030技术指导产品介绍产品名称：锥入度测定仪产品型号：A3030概 述：自动锥入度测定仪适用于石油、化工、冶金、电力、交通、商检及科研等部门。适用标准：GB／T 269仪器维护1、安装仪器时，必须平稳牢固。不准在潮湿，有腐蚀性气体的环境中存放或使用。2、本仪器在使用过程中如果出现故障，切勿乱拆乱动应请专业技术人员检修，或电告我厂，以便及时修理。3、本公司的仪器自发货之日起，一年内确属仪器本身的质量问题，免费保修。若由于是交通运输中出现的问题，协商解决，保修期已过的可提供收费服务。注意事项1、油样需在25℃环境中存放，试验。2、试验操作中，当将试样金属盛器放到针入度仪器的台面上时，应轻轻平放，不应与台面互相砸撞，有助于保持台面的水平。4、有释放针入件落下后，需要重新提起撞杆时，应先用手按松手动释放按钮，而不应在撞杆仍被锁紧的状态下进行用力抽拔，以免损伤撞杆表面和撞杆套的内孔。5、每次进行试验工作后，都应立即取下各种已装好撞杆上的标准针入件，并进行适当台面保护。6、各种选用的标准针入件，平时应上油保护，放入专用盒内。

傅立叶变换红外光谱法测定改性沥青中SBS改性剂含量解决方案 公路建设和养护对改性沥青的需求量上升，沥青改性技术也得到了日新月异的发展 ////////////SBS改性沥青是目前公路工程中用量最大的改性沥青品种，SBS的掺入，提高了沥青的高低温性能和弹性恢复性能。然而只有当基质沥青中SBS的掺入量达到合适的比例时，才能形成弹性稳定体系，发挥最好的路用性能，SBS的含量对SBS改性沥青的路用性能起着决定性影响。2019年交通运输部发布的最新一版《公路工程沥青及沥青混合料试验规程》中，改性沥青中SBS含量检测成为强检项目，傅立叶变换红外光谱法是唯一检测方法。北分瑞利行业解决方案目前傅立叶变换红外光谱法用于改性沥青中SBS含量检测时常用的测样方法如ATR法和窗片法，看似简单，实际上由于光程不固定等因素导致测试的重复性较差，对一线操作人员要求极高。而各个标准中都规定了多次测量的相对误差要控制在5%，这就使得一线操作人员在实际运用傅立叶变换红外光谱法进行改性沥青中SBS含量分析时经常需要反复重复测试，耗时耗力。本方案使用光程固定的液体池进行测样，方法重复性好、误差小，配合专用的沥青分析软件，能够实现改性沥青中SBS含量的快速、准确测量。标准依据及测试原理标准依据DB36/T 1131-2019 改性沥青中SBS、SBR类改性剂含量测定 红外光谱法DB33/T 989-2015 改性沥青中SBS含量的测定 红外光谱法JT/T 1177-2017 改性沥青SBS含量测定仪JTG E20-2019 公路工程沥青及沥青混合料试验规程 测试原理根据Lambert-Beer定律，利用待测物质特征官能团在特定波长（波数）处的红外吸收强度与物质浓度的正比关系，进行改性沥青中SBS含量测定。选取改性沥青红外光谱图中966cm-1处的C=C基团上碳氢键弯曲振动特征吸收峰（来源于SBS），和1377cm-1处的CH3基团上碳氢键弯曲振动特征吸收峰（来源于基质沥青），作为SBS含量测定的特征吸收峰。分别测量特征吸收峰面积（S966和S1377），计算两峰面积的比值（A），以比值（A）与SBS含量建立线性标准曲线。通过对待测改性沥青试样进行红外光谱检测、两特征峰面积测量以及比值（A）的计算，对照标准曲线，确定试样中SBS的含量。仪器设备与测试条件仪器设备_名称规格型号No.1主机WQF-530傅立叶变换红外光谱仪No.2主机WQF-1910便携式傅立叶变换红外光谱仪No.3软件MainFTOS Suite采集软件+傅立叶变换红外沥青测量系统No.4附件KBr液体池耗材试剂分析纯四氯化碳、不同SBS含量改性沥青标样。 测试条件波长范围4000~400cm-1；分辨率4cm-1；扫描次数16次。测试结果A值计算图 1 沥青专用软件计算A值示例图测试光谱数据直接导入傅立叶变换红外沥青测量系统专用软件自动计算A值，避免了繁琐的手工计算。标曲建立图 2 沥青专用软件建立标曲示例图傅立叶变换红外沥青测量系统专用软件具有自建标曲、未知样检测、报告输出和打印等功能，极大的提升了用户的工作效率。实验结论本方案使用固定光程液体池配合实验室/便携式傅立叶变换红外光谱仪进行改性沥青中SBS含量测定，方法重复性好，大大降低了一线操作人员的实操难度，节省了客户的人力成本；傅立叶变换红外沥青测量系统专用软件将A值计算、标曲建立和未知样检测等需要大量手工计算的工作全部自动化，避免了繁琐地手动计算过程，提高了客户的效率；所建标曲拟合度达到0.99以上，满足相关标准要求。

LUM集团在法国建立沥青和石油分析战略伙伴关系 柏林, 2021年11月9日: 2021年10月，LUM GmbH与法国VIALAB SARL建立长期战略合作伙伴关系，以便为法国客户提供更多沥青、石油和相关乳液领域的专业知识以及解决方案。在LUM法国分公司的协助下，VIALAB SARL将利用其在这一市场领域的专业知识以及渠道，大力推广LUM分析仪器的优势。 VIALAB SARL公司致力于生产和销售用于乳液参数检测的实验室设备，符合欧洲NF EN 13808标准和ASTM标准。Vialab还同时也运营自己的直属实验室，有针对性的对客户的乳化液试验系统进行相对应的技术培训。 LUM GmbH成立于1994年，总部位于柏林。LUM分别再在法国、美国、中国和日本设有分公司。LUM GmbH在以下领域拥有数十年的科学和计量专业知识： • 颗粒表征 • 悬浊液和乳液分析 • 检测粘结强度和剪切强度 • 质量控制和过程优化。 在石油和沥青乳液领域，LUMiReader PSA被广泛客户使用进行对沥青质表征，其检测方法基于ASTM D7827（通过光学装置检测重燃料油中正庚烷诱导的沥青质相分离作为可分离数的标准试验方法）。此外，根据ISO 13318，LUMiFuge和LUMiSizer能够快速直接进行稳定性分析和粒径分布测定。 LUM GmbH首席运营官Susanne Lerche Merchant陈述：“通过这一新的合作伙伴关系，我们将能更有效更针对性的接触石油和沥青领域的用户。我们正有计划的战略布局，将LUM各地的子公司发展成当地的运营中心。同时，由LUM 法国和VIALAB之间的这次密切合作，我们也看到了巨大的潜力。我们可以结合国际沥青乳液联合会成员VIALAB的专业知识和有效的渠道，开拓LUM仪器新的分析领域。”VIALAB首席执行官Vincent HESRY陈述：“向我们的客户提供由LUM GmbH开发的新技术，其前景看来令人很期待。我们致力于生产专门用于沥青粘合剂的实验室设备。我们相信，这种合作关系将使我们能够为客户带来更加有效的解决方案，为实践的发展做出更大的贡献。法国在这一领域是世界知名的参与者，而Vialab也希望参与新检测方法的研究和探讨，以改进基于纯粘合剂乳液（改性或甚至创新）的路面。” 附上的图片人物为: 左一：LUM法国 - Sylvain Gressier右一：VIALAB首席执行官 - Vincent Hesry

最近《This Old House》这档节目介绍了家居装修的内容，在该节目中，着重研究太阳能反射沥青瓦的特性。对这些瓦片进行了加速老化测试，以保证太阳能反射沥青瓦的反射性能。太阳能反射沥青瓦在家居装修的使用具有非常重要的作用，研究表面，建筑材料的选择对建筑物的导热性能非常重要，深色材料的太阳反射率比浅色材料的太阳反射率低，因此选择浅色建筑材料可以降低室内温度，在夏天这是非常重要的。屋瓦对室温温度起到了重要性作用。沥青瓦是是一种具有装饰和防水保温隔热功能的屋面材料，传统的沥青瓦由压在沥青玻璃纤维基材上的小岩石状颗粒制成，具有深色的外观，但具有低的太阳反射率。随着技术的发展，圣戈班等制造商研发了新型的太阳能反射沥青瓦，能保留深色外观的同时，提高太阳反射率，有效反射大部分红外光，具有以下的优点：1.沥青瓦可以抵御各种气候条件，如光照，雨水和冰冻等2.太阳能反射沥青瓦能保温隔热，在夏天阻断热量由外向内传导，在冬天防止热量由内向外散失3.耐腐蚀性，太阳能反射沥青瓦不会在酸雨等恶劣环境下，出现锈蚀、花斑现象然而沥青瓦也有一定的缺点，最大的缺点是易老化，因此对在沥青瓦投入市场使用之前对其进行老化测试非常重要。节目中，圣戈班代表详细介绍了使用QUV紫外老化试验箱对太阳能反射沥青瓦进行加速老化测试，详细说明了各种沥青瓦暴露在太阳辐射的情况，以及如何选择QUV老化测试循环周期更好模拟室外气候条件。翁开尔40年专业资深代理美国Q-LAB系列产品，欢迎致电咨询更多关于Q-LAB耐候老化测试箱，如紫外老化试验箱，氙灯老化试验箱，盐雾腐蚀试验箱等。

2023年8月初，欧美大地邀请了意大利CONTROLS公司的技术工程师Jesse Bedra来华进行了为期一周的内部培训。此次培训旨在进一步提高欧美大地国内技术服务团队对于UTM等沥青混合料多功能道路材料试验机的操作水平和培训水平，更好的服务国内客户。自欧美大地2018年成为意大利CONTROLS公司的中国合作伙伴以来，双方一直致力于提高为中国用户服务的水平，此次实地培训也是时隔3年，双方组织的一次重要技术培训活动。此次培训首先由Jesse在会议室内进行了动态试验机控制技术的理论培训，为大家深入讲解PID控制的理论和注意事项。随后的几天，在山东高速集团有限公司，山东建筑大学和山东省交通科学研究院3个用户的实验室内，使用各种类型的动态试验机（液压的UTM-30和UTM-130，电动的AsphaltQube），及传统的UTS软件和新版的UTS Neutron软件实际开展了多个试验方法的实际操作培训。在此次培训的试验方法中，不但选择了国内用户目前普遍熟悉的单轴压缩动态模量试验（JTG E20-T0738）和四点小梁弯曲疲劳寿命试验（JTG E20-T0739），还关注了其他应用不普遍，但今后可能借鉴的美国、欧洲的方法体系及欧美标准，并了解了低温性能试验新方法的研究进展。这三个方面的培训内容，即针对目前国内客户普遍关心的试验方法，又涵盖了沥青路面材料未来的研究发展方向，对于欧美大地更好的协助客户，推动创新研发起着重要作用。 方向1：欧盟方法欧盟在确定沥青路面材料设计参数时，除法国主要使用梯形梁2点弯曲试验方法外，其他主要使用间接拉伸的试验方法，2018年更新的EN 12697-26刚度模量试验方法中增加了方法F间接拉伸动态模量试验方法（德国AL-SP-Asphalt-09）。在评价疲劳性能时，则可以使用EN-12697-24疲劳试验方法中的方法E。与我国交通行业标准选择的单轴压缩动态模量和四点小梁疲劳试验方法相比，间接拉伸试验方法的主要优点在于试件获取更加方便，甚至能够直接使用现场取芯的试件和马歇尔试件进行试验。相比之下，单轴压缩动态模量和四点小梁弯曲疲劳的试件获取要麻烦一些，这也是目前制约方法推广普及的原因之一。因此，提高间接拉伸试验的操作和培训水平，有助于我们满足国内众多欧洲留学归来的专家学者的研究需要，也可以在部分情况下试件获取困难时使用现场芯样或马歇尔试件来对路面性能给予评价。间接拉伸试验（左-动态模量/右-疲劳寿命）方向2：美国方向继我们邀请Richard Kim教授在国内就基于AMPT的沥青混合料性能评价体系开展理论教学推广后，我们再次请Jesse就试验的实际操作进行了深入培训。而且，基于目前国内AMPT用户数量较少，而UTM类型的动态试验机较多的现状，我们此次培训AASHTO T400 S-VECD（原TP105，目前已成为正式试验标准）和AASHTO TP134 SSR试验是基于AsphaltQube和UTM试验机进行的，实测结果表明：即使用户没有AMPT，也可以成功开展相关试验研究。（AMPT作为开发整套体系的试验设备基础，操作上要更加方便）PASSFlexTM试验方法培训（左-SVECD/右-SSR）基于目前国内试验方法体系仍重视四点小梁疲劳试验，以及要兼顾低温性能评价的现状，资金预算有限的用户，可以考虑购买AsphaltQube系列电动多功能动态试验机。AsphaltQube系列通过将AMPT的三轴室改变为环境箱，增加了荷载量程（最大±30KN动态），扩大了温控范围（最大-40℃~+80℃），并可以进行四点小梁弯曲疲劳试验，以及低温性能试验。同时还具有环保，集成度高，移动性强，操作便利等优势，是用于替代UTM-30的动态试验机产品。电动型AsphaltQube动态试验机方向3：低温性能评价新方法目前我国行业标准中评价沥青混合料低温性能的试验方法是JTG E20 T0715沥青混合料弯曲试验方法，一般称作“三点小梁弯曲试验”。但该试验方法因为数据离散性大，业内同行普遍对这种试验方法感到不满意。因此，近年来国内外同行提出了多种试验方法希望替代三点小梁弯曲试验。这些主要的方法有：（1） AASHTO T394（原TP105） SCB，低温半圆弯曲试验；（2） AASHTO TP10-93 TSRST，约束试件温度应力试验；（3） ASTM D8303 UTSST，单轴温度应力应变试验；（4） ASTM D7313 DCT，碟型试件偏心拉伸试验；（5） EN 12697-46低温性能试验方法。 在这些方法中，我们主要选择了方法1和2作为了此次培训的主要内容。原因在于：（1） 低温SCB试验方法与DCT试验方法大同小异，都是基于断裂能理论来评价沥青混合料的低温性能。相比低温SCB，DCT试验方法目前没有进入AASHTO试验规范体系，试件制备过于复杂（需要特制的切缝机和钻芯机），全球应用也不够多。（2） TSRST试验方法在美国和欧盟都是行业标准的一部分，国内对此方法比较熟悉，有很多单位开展过相关研究。UTSST试验方法是在TSRST试验的基础上增加了测量沥青混合料在低温条件下无约束的收缩应变，因此，试验操作是类似的，理解了TSRST，也就理解了UTSST。低温性能试验方法培训（左-TSRST冻断/右-低温SCB）此次在山东高速集团有限公司，山东建筑大学和山东省交通科学研究院的3个实验室进行培训，使得制造商、技术服务工程师与用户，有了更多现场交流的机会。在欧美大地的技术服务团队加强了对动态试验机的理解、对以上试验方法的理解、提高了试验的操作水平、提高数据质量，为今后帮助用户充分挖掘设备潜能，顺利开展试验研究打下了坚实的基础的同时，还解答了全国用户遇到的各种问题。也与现场用户进行了沟通，加深了用户对于动态试验机的认知，对于将动态试验机更好的应用于沥青混合料未来发展与研究中，起到了积极作用。 结语：在此，感谢山东高速集团有限公司，山东建筑大学和山东省交通科学研究院3个用户在场地，设备，试件等基础条件方面的大力支持。如想进一步了解情况，请登录欧美大地仪器官网咨询。

能谱科技与山东青岛路桥建设集团有限公司携手合作，成功完成了一项关键的仪器安装项目。本次合作中，能谱科技为青岛路桥提供了先进的沥青红外光谱仪，为其沥青材料分析提供了强大的技术支持。 山东青岛路桥建设集团有限公司作为业内的路桥建设企业，一直致力于提升工程质量和技术水平。为了更精准地分析沥青材料的性能与质量，公司选择了能谱科技的沥青红外光谱仪作为关键测试设备。该仪器采用先进的红外光谱技术，能够快速、准确地分析沥青中的化学成分，为公司的材料选择和质量控制提供了有力支持。 在安装过程中，能谱科技的工程师团队展现了高超的技术水平和专业素养。他们严格按照安装规范进行操作，确保仪器能够稳定、高效地运行。同时，他们还根据用户的实际需求，对仪器进行了个性化的配置和优化，使其能够更好地满足公司的测试需求。 青岛路桥建设集团对能谱科技的现场仪器安装工作给予了高度评价。他们表示，能谱科技的技术人员专业熟练、细致周到，不仅迅速解决了安装过程中出现的问题，还提供了全面的操作培训和技术支持。这使得他们能够顺利开展沥青材料的分析测试工作，并获得了准确可靠的结果。 能谱科技拥有一支经验丰富、技术的团队，他们致力于为客户提供的服务和支持。此次合作再次证明了能谱科技在红外光谱应用领域的地位和专业水准。能谱科技将继续致力于为客户提供的仪器和优质的服务，为各行业的科研与生产工作提供有力支持。 如果您对能谱科技的沥青红外光谱仪或其他产品感兴趣，欢迎随时联系我们，了解更多详细信息。

近日，神木煤化工天元公司申请的“沥青取样器”实用新型专利获得国家知识产权局授权。至此，天元公司累计申请专利179件，获得授权专利130件，其中发明专利42件。一直以来，天元公司坚持把科技创新摆在企业高质量发展全局的核心位置，不断延伸煤炭及煤焦油深加工产业链条，形成了具有自身特色的煤炭清洁高效综合利用技术体系。持续强化知识产权创造、运用、管理和保护，建立了比较完善的知识产权管理体系，坚持将知识产权管理融入生产经营全过程、各环节，全力推动知识产权工作规范化实效化，企业竞争力及知识产权综合实力得到稳步提升。公司先后被认定为陕西省知识产权示范企业、中国石油和化工行业知识产权示范企业、国家知识产权优势企业。“一种煤热解提质一体化成套系统及工艺”荣获陕西省专利奖一等奖，“中温煤焦油生产针状焦关键技术研究与示范”荣获陕西省第二届秦创原高价值专利大赛优胜奖等。今后，天元公司将聚焦企业转型升级需要，加速推进创新成果向产业链高效转化，加快煤基精细化学品等核心产品技术攻关，不断提升产业价值链和产品附加值，以高水平科技创新助推企业实现高质量转型发展。

中小企业在确保国民经济适度增长、缓解就业压力、优化经济结构等方面的作用越来越重要，对整个国民经济更具有战略性。但中小企业发展现状面临的问题依然严重。中小企业总体素质较低、增长方式粗放、产品结构雷同，主业不突出，竞争力不强，依法经营、诚实守信意识淡薄；在协调配套生产、劳动密集型产业、服务业等可以发挥特色的领域发展不足。 　　无论大小企业，目的无非都是为了积极寻求发展。为扶持深圳本地仪器仪表中小企业健康、快速成长，6月23日，深圳市仪协特召开“深圳市仪器仪表与自动化行业沙龙会议”， 深圳市仪器仪表与自动化行业协会杜如彬执行会长兼秘书长及近百家企业参加了此沙龙。会议从政策讲解、融资、工业用地、转变生产方式等方面为行业内的企业理清自身发展中存在的突出问题，针对性地采取措施解决企业外部和内生的约束，有效帮助中小企业保持健康、持久的发展。 　　会议由深圳市仪器仪表与自动化行业协会秘书长助理黄艳聪先生主持，他表示，如今，政府及企业到个人都在提倡如节能减排，但如果没有仪器仪表、传感器、变频器这些低碳技术做为基础，智能电网、物联网、低碳经济、节能减排无从谈及，虽然仪器仪表行业迎来好的机遇，国内外经济形势渐好，但不得不承认，民营中小企业在发民过程中面临物料成本，人工成本上升、工业用地困难、融资难等诸多问题。 　　深圳市中小企业服务中心副主任杨宇清先生首先就民营及中小企业发展专项资金管理与使用说明及申请条件、流程等进行了演讲，他表示，深圳市政府推出了一系列如人才培训、企业基地、创业板等针对中小企业的扶持政策。但大部分中小企业对政府政策不够关注、不同步。有些企业，明明在符合政府中小企业资金申请资格，但公司负责人对此事并不关注，结果错失好机会。杨宇清先生提醒仪器仪表民营中小企业，在忙生产、忙技术、忙管理的同时，还要关注政府政策。实施政府“两化”政策，做成像中兴、华为等有影响力的企业。 　　深圳发展银行深圳分行贸易融资部副总经理李博对深圳市中小企业融资难进行了分析。 　　深圳市航工业地产投资发展有限公司经理杨青先生就企业工业用地需求进行演讲，他表明，深圳市仪器仪表中小型企业大可不必在深圳市内狭小空间互挤，可朝周边如惠东等区域发展。 　　会议最后由中国产业转移发展促进会副会长、中国移动营销工程师、国际注册法律顾问师刘耕伯先生发表“三网融合，中国产业变革之路”的演讲作为结束。

国家标准《石油蜡针入度测定法》由TC280（全国石油产品和润滑剂标准化技术委员会）归口上报，TC280SC3（全国石油产品和润滑剂标准化技术委员会石油蜡类产品分会）执行，主管部门为国家标准化管理委员会。本标准将于2022年5月1日正式实施，主要起草单位：中国石油化工股份有限公司大连石油化工研究院、中国石油化工股份有限公司荆门分公司、中国石油化工股份有限公司茂名分公司、中国石油天然气股份有限公司大连石化分公司、中国石油天然气股份有限公司抚顺石化分公司、辽宁省检验检测认证中心。主要起草人：郭士刚、王少军、高旭锋、凌凤香、张会成、蒋秀华、刘锦凤、于锡闻、吕申宏、段卫宇。本文由标准由中国石化大连石油化工研究院首席专家 张会成著，文章禁止任何形式的转载、摘录，违者必究。一、修订背景石油蜡针入度是在规定条件下标准针刺入蜡试样的深度，是石油蜡硬度的测量结果，影响到蜡的使用性能。GB/T 4985-2010随着形势发展已不能满足指标表征的需要：一是蜡的来源渠道增加，市场出现非天然石油蜡蜡等产品；二是GB/T 254《半精炼石蜡》、NB/SH/T 0013《微晶蜡》中含有35℃下针入度指标，而方法中未规定测定精密度，市场又出现了40℃针入度要求；三是部分石油蜡产品25℃下针入度不能充分区分产品性能；四是方法中缺乏自动化仪器操作过程，而市场用户已普遍使用；五是我国是蜡生产大国，更是蜡出口大国，但不是标准强国，执行标准需紧跟国际先进标准或严于先进标准。满足要求的修订标准已发布实施。不同试验温度针入度，1/10mm样品25℃30℃35℃40℃45℃半精炼蜡60#1523314871半精炼蜡54#183977139163全精炼蜡64#1619233244微晶蜡70#1922324968 二、修订的技术内容标准主要修订技术内容：1.增加了费托蜡、合成蜡、生物蜡等产品；2.增加了自动针入度计的试验过程；3.修订了制样试验温度；4.增加了质量控制内容；5.增加了35℃、40℃下结果精密度。标准主要技术变化GB/T 4985-2010GB/T 4985-2021适用范围石油蜡石油蜡、费托蜡、合成蜡、生物蜡仪器设备手动针入度计手动针入度计、自动针入度计制样温度23.9℃±2.2℃24.0℃±2.0℃质量控制无增加了质量控制要求精密度25℃精密度25℃、35℃、40℃下精密度三、修订过程大连石油化工研究院负责起草，组织6家单位参与，共使用5种自动和手动设备，10个样品包括全精炼蜡、半精炼蜡、粗石蜡、工业石蜡、食品添加剂石蜡、费托蜡、石蜡，测定结果使用GB/T 6683进行数据处理，获得精密度。四、试验过程注意事项1、仪器调节：水准仪保证标准针垂直，脱落无明显阻力。2、零”点调节：自动设备科自动零点调节，手动设备可以转动数字表盘达到指针指“0”，也可以记录指针位置作为相对零点，用减差法计算针入度。3、水浴控制：温度变化控制在±0.1 ℃以内，水液面高于试样上表面25mm。4、温度测量：全浸型温度计保证水液面高于水银柱，必要时需进行校正。5、精密温度计、标准针、秒表须检定校准并实验室确认。

执行国家标准GB/T269。广泛适用于石油、化工、冶金、电力、交通、商检及科研等部门。核心主机采用TI 公司AM3354处理器，Cortex-A8内核，1GHz主频；操作系统采用Windows Embedded Compact 7实时工控系统。彻底摈弃了无核无操裸奔的单片机，真正实现了仪器操控的现代化，使仪器步入新的智能时代显示器采用群创原装7.0英寸800×480像素LCD液晶显示屏，全中文操作界面，显示细腻直观大方。操作采用电容式触摸屏,其优点在于无机械损耗、防尘防水、抗射频干扰、使用寿命长。历史数据存储采用FLASH数据存储器存储，可存储2010个历史数据，数据可保存10年不丢失，储存数据不可更改。后置USB，后期软件更新电，以及仪器维护检查，可连接鼠标键盘操作打印机可选择采用嵌入式热敏、可选装针式打印机，打印更安静、快速、清晰（可选装针式打印机）。锥入度检测采用无接触位移检测技术，使锥体移动瞬间快速准确捕获，在测试过程中完全避免了误检与漏检。具备自动提起，自动释放，自动测定,自动打印测试结果,零点调整等功能零点自动追踪，实验过程自动找寻零点，自动回位试样杯面与锥尖的基础面，免去每次实验时都要对平面的烦恼，提高实验效率。内部机械部分均采用防腐防锈高强度304不锈钢材料打造，更耐用使用寿命更长。可拆卸式锥杆，方便工作人员做精密测试。仪器标配全尺寸锥，可加装1/2锥，1/4锥功能为单独仪器配置仪器支持送检对其精度、锥杆质量以及椎体质量出具资格证书（检测费用自费）。 参数：测量范围：0～640个锥入度单位(全尺寸测量范围)标准锥及牵引锥杆质量：全尺寸锥：标准锥质量:102.5±0.05g（符合国家标准GB/T269的规格要求）牵引锥杆质量:47.5±0.05g（符合国家标准GB/T269的规格要求）总重150±0.05g1/2尺寸锥：标准锥质量:22.5±0.025g（符合国家标准GB/T269的规格要求）牵引锥杆质量:15±0.25g（符合国家标准GB/T269的规格要求）总重37.5 ±0.06g1/4尺寸锥：锥体和可移动附件总质量为9.38g±0.025容器尺寸：（全自尺寸、1/2 1/4容器）石油脂试料容器:直径φ100±0.6mm 高：≥65mm(内径)润滑脂试料容器:直径φ76.2±0.6mm 高: ≥65mm(内径)测量精度：1个锥入度单位释放时间：5S时间控制：自动环境温度：10℃～45℃ 环境湿度：≤85%操作方式：触摸屏操作，使用简便，操作更加直观电源电压：220±10% V.AC电源频率：50±10% Hz消耗功率：100W外形尺寸： 580mm（L）×370mm（W）×590mm（Ｈ）仪器重量：25Kg 创新点：市面所销售锥入度仪器多为手动1/4锥测定仪，我司设计产品为全自动1/4锥入度测定仪，可自行零点自动追踪、自动提起、自动释放、自动测定、自动打印测试结果等功能，而市面所销售均为全尺寸自动锥入度，全自动1/4Z锥测定仪具有一定义填补空白市场 1/4锥入度试验仪

近年来，随着公路工程的迅速发展，沥青供应市场也愈发的混杂，需要对沥青质量沥青进行进一步地质量控制。传统试验依赖试验人员的专业水平和仪器设备的准确性，耗时较长，稳定性较差。如今，道路工作者发现无论是基质沥青还是SBS改性沥青三大指标都满足规范要求，但是越来越接近规范控制下限，沥青在日后的抗老化性能中表现较差，短时间内即出现老化、开裂、坑槽、车辙等病害，严重影响了行车的安全性和舒适性。如何辨别真假沥青？现在通过沥青指纹识别技术一测即可获得结果。由浙江道路养护工程技术研究中心引进能谱科技沥青指纹识别技术，通过该技术对工程项目进场沥青进行检测，能够可靠的鉴别基质沥青的品质，确保了进场沥青的质量。近日，工程技术研究中心技术人员赴在建项目利用该技术对2019年进厂沥青逐车进行了检测，检测结果全部匹配。　　能谱科技HWLQ-1红外光谱沥青分析系统是利用iCAN 9傅里叶变换红外光谱仪（iCAN 8 Plus便携式红外光谱仪）采集沥青的红外谱图，以确定沥青样品的分子结构和特定化学结构的精确含量，并与数据库中的沥青标准样品红外谱图进行比对，从而实现沥青品牌的快速识别，杜绝沥青混兑、掺假或以次充好。通过供货样品与施工现场使用沥青的两种指纹图表信息认真对比，即可得知样品与现场使用的沥青指纹信息是否吻合。同时，该技术相比传统的试验检测手段具有识别精度高，人为干扰小等优点，且整个检测过程仅需5分钟，大幅度提高了试验检测效率，市场前景十分广阔。　　浙江道路养护工程技术研究中心下一步将对该技术进行吸收转化、二次创新，并逐步在浙江省内进行推广应用，旨在进一步加强沥青质量控制，提高路面工程质量提供有力的技术支撑。 天津能谱科技服务于国内广大科研院所和工业客户，对先进的行业应用和市场需求有丰富的认识和理解，所以，我们提供给客户的，不仅仅是一台傅立叶红外光谱仪，更是一套完整的解决方案：从样品预处理到采样方案，从现场设计到后期的项目实施，我们都可以为客户提供个性化解决方案和完整的项目体验。　　天津能谱科技研发及销售团队成员有丰富的业内经验和专业的技术背景，对市场的需求有长期而准确的理解，大家有着一致的理念和目标，配合默契，服务高效。

1.试件破型室，主要有水泥胶砂抗折抗压试验机、全自动压力试验机等主要试验设备，均采用微机测控系统，自动采集处理打印试验数据，提高工作效率和试验准确性，可以完成水泥混凝土强度、水泥胶砂抗折强度的试验。2.水泥室，主要有水泥净浆搅拌机、胶砂搅拌机、自动标准养护水箱、水泥胶砂流动度测定仪、胶砂试件成型振动台、标准养护箱、电动抗折试验机、负压筛析仪等十余台主要试验设备，可以完成水泥凝结时间、安定性、强度、细度等各项性能指标的测定。3.集料室，主要有砂当量测定仪、棱角性测定仪、电子静水天平、加速磨光机、洛杉矶磨耗机、顶击式两用振筛机、电热鼓风干燥箱等主要设备，可以完成集料的筛分、表观相对密度、含泥量、棱角性、砂当量的试验。在各种配合比试验中，比如水泥混凝土配合比，沥青混合料配合比等都需要用到集料，所以利用率较高。4.土工室，土工试验的基础配备我们已经比较完善齐全，像主要有高温炉、电动液压脱模器、电动击实仪、顶击式两用振筛机、数显路强仪、液塑限联合测定仪、电热鼓风干燥箱等主要设备。土的各项物性、塑性指标比如：z佳含水量、z大干密度、密度、含水率、颗粒分析、界限含水量、承载比CBR、烧失量都可以进行检测。在公路工程施工过程中必须要进行土的各项试验检测，实验室的仪器设备、人员配备以及检测能力都可以满足日常公路工程试验检测的要求。5.化学分析室，主要有酸度计、滴定设备、干燥器、电子分析天平等主要设备，可以完成混凝土用水的PH值、氯化物含量、石灰钙镁含量、灰剂量的试验。按照标准实验室要求，药品管理严格规范，双人双锁。天平室配有两个万分之一和一个千分之一的精密天平，为保证其精que性，单独隔间，恒温管理。6.沥青室，主要低温恒温水浴、沥青脆点仪、沥青旋转薄膜烘箱、沥青闪点试验仪、全自动沥青软化点试验仪、针入度试验仪、延度仪、真空干燥器等主要设备，可以完成道路石油沥青的各项性能指标，如针入度、延度、软化点、密度、闪点、溶解度、耐老化性、粘附性等的试验。沥青试验危险性高，散发有毒气体，所以在试验时均需佩戴防毒面具。因为考虑到沥青检验室可能产生的废气、烟雾等收集、排放、处理，可以将各个主要设备加盖工作间，进行隔离操作，防止气味蔓延。7.沥青混合料室，主要有沥青混合料理论z大相对密度试验仪、液压车辙试样成型机、自动车辙试验仪、电热鼓风干燥箱、自动混合料拌和机、马歇尔稳定度试验仪、数显马歇尔击实仪、燃烧炉、恒温水浴、电动液压脱模器等十余套主要仪器设备，可以完成沥青混合料配合比设计、密度、马歇尔稳定度、沥青含量、矿料级配、z大理论密度、高温稳定性等试验。 8.力学室，主要有300 T、200 T 、150 T 、100 T 、80 T 、50 T、20 T 、10T、5T、2 T、1 T、0.5 T各种量程和精度的全自动微机控制w能材料试验机、拉力试验机、钢筋弯曲机等主要仪器设备，可以完成屈服强度、抗拉强度、断后伸长率、弯曲性能、表面质量、重量偏差、屈强比等试验。 9.交通工程室，配有先进仪器桩身完整性测试仪，可以应用低应变反射波法检测桩身完整性；钢筋探测仪可检测钢筋保护层厚度和钢筋直径，这两套设备属于进口精密仪器。另有国内先进的桩基静载荷测试分析仪、多通道声波透射法自动测桩仪、非金属超声波检测仪等设备可完成桩基检测。在路基路面现场检测中，配有路面平整度仪、路面弯沉仪、摆式摩擦系数测定仪等主要设备，可完成公路几何尺寸、路面厚度、压实度、构造深度、渗水系数、摩擦系数的试验。此实验室主要是完成现场检测，每台仪器设备外出工作都要有出库记录，严格按照试验规范进行操作。10.水泥混凝土室，此实验室主要是进行水泥混凝土配合比设计、砂浆配合比设计，以及进行水泥混凝土和砂浆的各项性能检测，比如稠度、凝结时间、表观密度、含气量、抗渗性能、立方体抗压强度、抗折强度、劈裂抗拉强度等，仪器设备比较齐全，主要有数显砂浆稠度仪、混凝土自动调压渗透仪、振动台、水泥混凝土搅拌机、砂浆搅拌机、耐磨试验机、数显混凝土贯入阻力仪等。

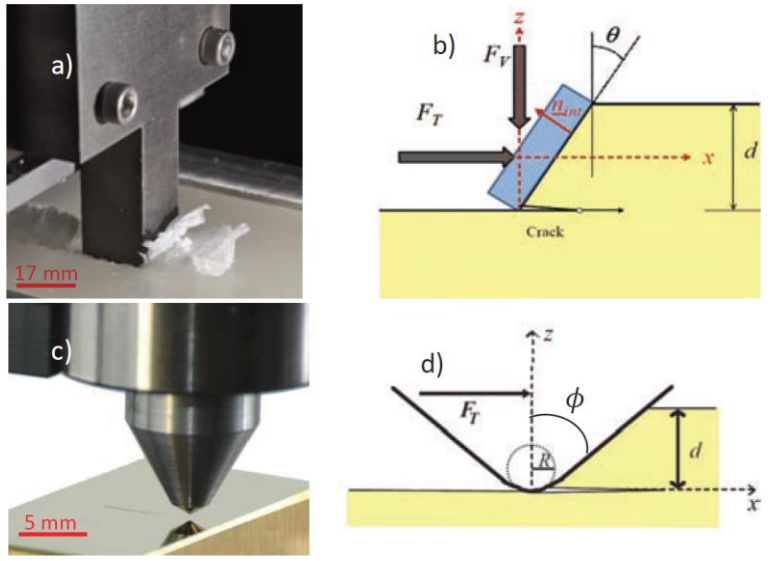
仪器化划入方法已经成功应用于测试各种材料（包括硬的合金、陶瓷、金属、岩石[1]和软的高分子聚合物、碱硅酸盐凝胶[2]等）的断裂韧度（跨越两个数量级）在材料科学与工程领域具有巨大应用前景，尤其是评估微米级材料或多尺度复合材料（比如碎屑-橡胶混凝土[3]、再生混凝土[4]、水泥[5]、页岩[1, 6, 7]，骨头[8]、功能梯度和复合涂层[9]）的断裂性能，其诸多优势包括：结果与传统方法（比如单边缺口试样的三点弯曲、紧凑拉伸）测量值一致；重复性好；材料体积小；设备操作、数据分析简单；近乎无损检测（微米级划入测试划入深度一般在十几微米）；尤其是试样制备简单，不需要预制缺口或裂纹；测试成本和周期都大大减小[10]。仪器化划入过程的实物图和示意图见图 1[11]。在仪器化划入过程中，利用侧向力和压入深度可以计算出材料的断裂韧度。仪器化划入表征断裂韧度主要有两种理论：一种是线弹性断裂力学（linear elastic fracture mechanics or LEFM）；另一种是能量尺寸效应理论（microscopic energetic size effect laws or ESEL）。理论都是假设在压头前端存在沿水平扩展的裂纹，见图 2[12]。这种裂纹模式在直刚刀压头划入石蜡的实验中体现得最好，见图 3[13]。对于直压头：三维裂纹的横截面是长方形。能量释放率可以由J-积分计算，再结合断裂准则，即可以建立利用侧向力和压入深度计算断裂韧度的关系式。图 1 仪器化划入测试实物图及示意图：（a）直钢刀压头划入石蜡；（b）倾斜直钢刀压头划入测试示意图；（c）Rockwell C压头划入薄膜材料；（d）轴对称压头划入示意图（压入深度d，压头尖端圆角半径R，侧向力FT，划痕方向x）图 2 利用轴对称压头划入过程的侧视图（左图）和正视图（右图）。x 是划痕方向，FT 是水平侧向力，FV 是竖直正压力，d 是压入深度，n 是压头与材料接触界面朝材料外侧的单位法向，A 是承载侧向力的面积投影，p 是压头与材料接触界面的周长图 3 石蜡在直钢刀压头仪器化划入过程中压头前端水平扩展的裂纹：（a）实验结果；（b）理想的裂纹形状示意图（具有长方形横截面的三维裂纹，需要裂纹长度l、刀具宽度w、压入深度d 三个尺寸表征）不同的学者提出了不同的分析方法，断裂韧度Kc 可以通过拟合仪器化划入的实验数据获得[10, 14-19]：其中Λ=A/(2P)是名义长度，p 和A 分别是周长和水平投影面积（见图 2），都是压入深度d 的函数[12]。利用线弹性断裂力学可以直接计算出断裂韧度Kc已知压头几何形状可以得到p(d)和A(d)，f=2p(d)A(d) 即压头形状函数：对于圆锥压头，f 与d3 成正比；对于圆球压头，f 与d2 成正比。图 4是利用Rockwell C压头划入钢材的结果[20]。示意图见图 4（a）。在划入过程中，施加线性增大的正压力FV，如图 4（b），同时记录侧向力FT 和压入深度d。数据与划痕残余形貌一一对应，形貌见图 4（c），并且可以利用声发射分析断裂过程，如图 4（d）。图 4 利用圆锥压头分析钢材料的断裂韧度：（a）圆锥压头仪器化划入过程示意图（划痕方向沿X 轴，FV 和FT 分别是正压力和侧向力）；（b）划入过程中在施加线性加载的正压力的同时记录侧向力；（c）划痕残余形貌；（d）侧向力和压入深度的关系（左轴）和声发射（右轴）当圆锥部分起主导作用时，FT/d3/2趋近于一条水平线，这说明划入过程由断裂机制控制，声发射信号也直接验证了断裂的发生。可见，利用划入方法测试材料的断裂韧度需要适合的加载条件，只有当载荷足够大，断裂机制占主导时才能应用线弹性断裂力学的公式计算断裂韧度，但是过大的载荷会产生很多扩展方向不同的裂纹，使得只有一条裂纹扩展的假设不成立。声发射信号是确定断裂发生的有效手段，可以用于区分断裂的程度（剧烈的断裂会使得声发射信号饱和），寻找适合的加载力范围。FT/d3/2一直在波动，这种锯齿状数据是切削的典型特征，与传统测试（比如紧凑拉伸中只有一个裂纹产生）明显不同，划入过程中会产生很多裂纹，所以有必要对平稳段的数据取平均[21]。仪器化划入方法已经成功应用于各种材料的断裂韧度表征[22, 23]，比如：高分子材料（聚碳酸酯PC[18]、改性石墨烯添加的环氧树脂基复合材料[24]）、玻璃（熔融石英硅[25]、K9玻璃[26]）、金属（紫铜[27, 28]）、半导体材料（单晶硅和碳化硅[29]）等。表 1比较了部分材料的仪器化划入测试结果与传统方法测试结果，划入法测试与传统方法测试结果大体一致，差异很有可能是由于材料的各向异性和不均匀造成的，因为划入法表征的是表面微观区域的力学性能，传统方法测试的是宏观力学性能。所以划入法可以表征材料断裂韧度的分布，适合于异质复合材料各组织以及界面的力学性能表征，研究不同尺度结构的断裂性能，这些都是先进材料及微纳米器件发展迫切需要解决的关键测试表征技术，尤其在表面微观力学领域有广阔的应用前景。表 1 利用仪器化划入方法表征各种材料的断裂韧度（MPa• m1/2）压头（形状尺寸）及方法材料（牌号）：划入法测的断裂韧度（传统方法测试值）单位（国家）[参考文献]Rockwell C压头（2θ=120°，R=200 μm），线弹性断裂力学铝合金(AA 2024)：34.4±3 (32~37)热塑性聚合物（Delrin Grade 150）：2.5±0.2 (2.9±0.5)麻省理工学院（美国）[20] Rockwell C 压头（2θ=120°，R=200 μm），线弹性断裂力学钠钙玻璃：0.71±0.03 (0.70)耐热高硼硅玻璃：0.68±0.02 (0.63)热塑性聚合物(Delrin 150E) ：2.75±0.05 (2.8)热塑聚碳酸酯：2.76±0.02 (2.69)铝合金(2024-T4/T351) ：28.8±1.3 (26~37)AISI-1045：62.2±2.6 (50)AISI-1144：62.2±2.6 (57~67)Titanium 6Al-4V：77.0±3.4 (75)麻省理工学院（美国）[22]直钢刀压头，线弹性断裂力学（LEFM）和能量尺寸效应方法(ESEL)石蜡：0.14 (0.15)水泥：0.66~0.67 (0.62-0.66)侏罗纪石灰岩：0.56 (ESEL), 0.34 (LEFM)A-51w：0.82 (ESEL), 0.81 (LEFM)B-4w：0.74 (ESEL), 0.72 (LEFM)B-12w：0.78 (ESEL), 0.78 (LEFM)麻省理工学院（美国）西北大学（美国）伊利诺伊大学厄巴纳-香槟分校（美国）[21]直钢刀压头、Rockwell C线弹性断裂力学水泥（直钢刀压头）：0.66±0.05 (0.67)钢材（Rockwell C压头）：40±0.2 (50)麻省理工学院（美国）[11]直钢刀压头能量尺寸效应方法水泥：0.66(0.65~0.67)伊利诺伊大学厄巴纳-香槟分校（美国）[23]Rockwell C压头线弹性断裂力学（LEFM）和能量尺寸效应方法(ESEL)塑料（Delrin）：3.26 (LEFM)，2.85 (ESEL)聚碳酸酯（Lexan）：2.87 (LEFM)，2.38 (ESEL)熔融石英硅：0.96 (LEFM)，0.96 (ESEL)传统测试结果：塑料（2.8）、聚碳酸酯（2.2）、熔融石英硅（0.8）科罗拉多大学（美国）麻省理工学院（美国）[28]Rockwell C压头能量尺寸效应方法聚缩醛 ：3.16 (2.8)石蜡：0.14 (0.14)聚碳酸酯（Lexan 934）：2.8 (2.69)铝：32.53 (32)伊利诺伊大学厄巴纳-香槟分校（美国）[40]圆球压头线弹性断裂力学熔融石英硅：0.7 (0.68~0.75)K9玻璃：0.85 (0.82)福州大学（中国）[45,46]Rockwell C压头线弹性断裂力学聚碳酸酯：2.3 (2.2)福州大学（中国）[43]作者简介刘明，福州大学机械工程及自动化学院教授，福建省闽江学者特聘教授、福州大学旗山学者海外人才、福建省高层次境外引进C类人才，全国钢标准化技术委员会力学及工艺性能试验方法分技术委员会金属材料微试样力学性能试验方法工作组（SAC/TC183/SC4/WG1）委员、ISO 14577系列国际标准制修订国内工作组成员。1985年出生于哈尔滨市，哈尔滨工业大学本科、硕士，肯塔基大学（美国）博士，法国巴黎高科矿业工程师学校材料研究所博士后、华盛顿州立大学（美国）博士后。主要研究领域为微观力学及仪器化压入划入测试方法。作者邮箱：mingliu@fzu.edu.cn 参考文献[1] A.-T. Akono, P. Kabir, Microscopic fracture characterization of gas shale via scratch testing, Mechanics Research Communications, 78 (2016) 86-92.[2] C.V. Johnson, J. Chen, N.P. Hasparyk, P.J.M. Monteiro, A.T. Akono, Fracture properties of the alkali silicate gel using microscopic scratch testing, Cement and Concrete Composites, 79 (2017) 71-75.[3] A.-T. Akono, J. Chen, S. Kaewunruen, Friction and fracture characteristics of engineered crumb-rubber concrete at microscopic lengthscale, Construction and Building Materials, 175 (2018) 735-745.[4] A.-T. Akono, J. Chen, M. Zhan, S.P. Shah, Basic creep and fracture response of fine recycled aggregate concrete, Construction and Building Materials, 266 (2021) 121107.[5] J. Liu, Q. Zeng, S. Xu, The state-of-art in characterizing the micro/nano-structure and mechanical properties of cement-based materials via scratch test, Construction and Building Materials, 254 (2020) 119255.[6] M.H. Hubler, F.-J. Ulm, Size-Effect Law for Scratch Tests of Axisymmetric Shape, Journal of EngineeringMechanics, 142 (2016).[7] A.-T. Akono, Energetic Size Effect Law at the Microscopic Scale: Application to Progressive-Load Scratch Testing, Journal of Nanomechanics and Micromechanics, 6 (2016) 04016001.[8] A. Kataruka, K. Mendu, O. Okeoghene, J. Puthuvelil, A.-T. Akono, Microscopic assessment of bone toughness using scratch tests, Bone Reports, 6 (2017) 17-25.[9] H. Farnoush, J. Aghazadeh Mohandesi, H. Cimenoglu, Micro-scratch and corrosion behavior of functionally graded HA-TiO2 nanostructured composite coatings fabricated by electrophoretic deposition, J Mech Behav Biomed Mater, 46 (2015) 31-40.[10] A.T. Akono, N.X. Randall, F.J. Ulm, Experimental determination of the fracture toughness via microscratch tests: Application to polymers, ceramics, and metals, J. Mater. Res., 27 (2012) 485-493.[11] A.-T. Akono, F.-J. Ulm, An improved technique for characterizing the fracture toughness via scratch test experiments, Wear, 313 (2014) 117-124.[12] A.T. Akono, F.J. Ulm, Fracture scaling relations for scratch tests of axisymmetric shape, J. Mech. Phys. Solids, 60 (2012) 379-390.[13] A.-T. Akono, F.-J. Ulm, Z.P. Bažant, Discussion: Strength-to-fracture scaling in scratching, Eng. Fract. Mech., 119 (2014) 21-28.[14] G.I. Barenblatt, The mathematical theory of equilibrium cracks in brittle fracture, in: H.L. Dryden, T. von Kármán, G. Kuerti, F.H. van den Dungen, L. Howarth (Eds.) Advances in Applied Mechanics, Elsevier, 1962, pp. 55-129.[15] H.M. Hubler, F.-J. Ulm, Size-effect law for scratch tests of axisymmetric shape, J. Eng. Mech., 142 (2016) 04016094.[16] A.-T. Akono, Energetic size effect law at the microscopic scale: Application to progressive-load scratch testing, J. Nanomech. Micromech., 6 (2016) 04016001.[17] D. Zhang, Y. Sun, C. Gao, M. Liu, Measurement of fracture toughness of copper via constant-load microscratch with a spherical indenter, Wear, 444–445 (2019) 203158.[18] M. Liu, S. Yang, C. Gao, Scratch behavior of polycarbonate by Rockwell C diamond indenter under progressive loading, Polymer Testing, 90 (2020) 106643.[19] M. Liu, Microscratch of copper by a Rockwell C diamond indenter under a constant load, Nanotechnol. Precis. Eng., 4 (2021) 033003.[20] A.T. Akono, P.M. Reis, F.J. Ulm, Scratching as a Fracture Process: From Butter to Steel, Phys. Rev. Lett., 106 (2011) 204302.[21] A.-T. Akono, G.A. Bouché, Rebuttal: Shallow and deep scratch tests as powerful alternatives to assess the fracture properties of quasi-brittle materials, Eng. Fract. Mech., 158 (2016) 23-38.[22] 刘明, 李烁, 高诚辉, 利用圆锥压头微米划痕测试材料断裂韧性, 摩擦学学报, 39 (2019) 556-564.[23] 刘明, 李烁, 高诚辉, 利用微米划痕研究TiN涂层的失效机理, 计量学报, 41 (2020) 696-703.[24] S. Li, J. Zhang, M. Liu, R. Wang, L. Wu, Influence of polyethyleneimine functionalized graphene on tribological behavior of epoxy composite, Polymer Bulletin, (2020).[25] M. Liu, Q. Zheng, C. Gao, Sliding of a diamond sphere on fused silica under ramping load, Materials Today Communications, 25 (2020) 101684.[26] M. Liu, J. Wu, C. Gao, Sliding of a diamond sphere on K9 glass under progressive load, Journal of Non-Crystalline Solids, 526 (2019) 119711.[27] D. Zhang, Y. Sun, C. Gao, M. Liu, Measurement of fracture toughness of copper via constant-load microscratch with a spherical indenter,Wear, 444-445 (2020) 203158.[28] C. Gao, M. Liu, Effects of normal load on the coefficient of friction by microscratch test of copper with a spherical indenter, Tribology Letters, 67 (2019) 8.[29] 刘明, 侯冬杨, 高诚辉, 利用维氏和玻氏压头表征半导体材料断裂韧性, 力学学报, 53 (2021) 413-423.

p 　　2016第8届华中武汉科学仪器及实验室装备展览会暨无损检测展，将于11月10-12日在武汉国际博览中心(汉阳)举办。目前，组委会客服推广部正在进行深入邀约专业观众参观工作。参观预登记如火如荼。 /p p 　　目前，有关建设工程检测的需求突出，更有几家湖北XX建设工程检测有限公司对购买“建筑工程检测仪器设备”求贤如渴，列出产品清单： /p p 　　1、建筑主体结构现场检测设备：回弹仪、超声波测试仪、钻芯机、原位压力机、钢筋保护层测定仪等 2、钢结构工程检测设备：超声波探伤仪、覆层测厚仪、WE-1000型万能试验机、轴力测试仪、扭矩测试仪等 3、建筑节能检测设备：智能门窗物理性能检测仪、耐侯性试验设备、智能门窗物理性能检测仪、重物荷载、抗拔仪、建筑门窗墙体传热系数检测设备、导热系数测定仪等 4、室内环境检测设备：测氡仪、甲醛测定仪、分光光度计、气相色谱仪、低成本多道Ã 能谱仪、环境仓、分光光度计、干燥箱等 5、设备安装工程检测：水压试压泵、绝缘电阻测试仪、接地电阻测试仪、微压计、风速仪、流量计、声强计、试压泵等 6、水泥物理力学性能检验：负压筛、天平、养护箱、抗折仪、恒速压力机、标准养护室(箱) 7、混凝土、砂浆配合比试配试验：搅拌机、维勃稠度仪、贯入阻力仪、压力泌水仪、振实台、标准养护室(自动温湿度控制)、砂浆搅拌机、分层度测定仪 8、沥青、沥青混合料试验：针入度仪、延度仪软化点测定仪、压力机、马歇尔稳定度仪、沥青混合搅拌机 9、建筑防水卷材试验：拉力机、柔度弯曲器、不透水仪 10、路面弯沉试验：弯沉仪 11、测绘勘探仪器 12、材料力学性能试验设备、无损检测仪器。 /p p 　　据悉，湖北省建筑产业总值迈入万亿行列，排在全国第三位。随之相应的建筑建材检测行业也飞速发展，相关建筑建材行业的检测仪器出现巨大需求，这将成为本届展览会的热点之一。(热线电话：张凯 13971153732 QQ：272265529) /p p br/ /p