高端多功能成像系统

FluorChem M 多色荧光、化学发光凝胶成像系统是美国ProteinSimple公司（原Alpha Innotech公司）最新推出的高端多功能成像系统。 FluorChem M的推出，为定量分析多色荧光Western Blot和凝胶成像设立了一套新标准。 具有多色荧光、化学发光、凝胶成像功能；支持印迹膜、核酸胶，蛋白胶、多孔板、培养皿等样品类型。 &bull 采用独特的一体式设计，触摸屏控制，支持远程操作 &bull 配合最先进的CCD光学技术，830万像素，3326x 2504分辨率，提供无与伦比的图像质量 &bull 10位滤光片轮，满足大部分图像检测应用 &bull 多色激发光源，专为Western Blot成像优化 &bull 摆脱暗室，超高灵敏度、快速成像、宽动态范围 &bull 预设多种程序，一键敲击即可成像，操作简单，无需培训 FCM特有的设计保证了其出众的多色荧光，化学发光凝胶成像性能，成为高端实验技术平台的首选. 原Alpha Innotech公司创立于1982年，总部位于美国加州，2005年上市，2009年12月被美国ProteinSimple公司（简称PS公司）收购。Alpha Innotech在数字化凝胶成像领域有20年的成功历史，用户超过20000个，引用的文献近10000篇。在凝胶成像领域处于领先地位，是高端多色荧光和化学发光技术的全球领导者。 PS公司总部位于美国硅谷，是世界一流的生命科学仪器制造商，专注于蛋白质研究分析领域，在美国加州、加拿大多伦多、加拿大渥太华等地设有生产和研发部门，同时在全球多地设有办事处。 更多信息请访问 http://china.proteinsimple.com/ 或致电 4000-863-973

2019年10月Azure产品全新升级，我们新推出的基于CCD的凝胶和蛋白荧光印迹多功能成像系统将客户所期望的高性能尖端技术与最新的严格标准定量方法相结合，全新升级系统，设计更紧凑，界面更时尚，性能更优越，定量更精准。创新点：Azure Imager多功能分子成像系统是整合一体机设计，13.3英寸触摸屏，2min完成深度制冷，可完成NIR双激光检测； RGB可见荧光检测，全蛋白定量，满足期刊杂志发表要求；快速高灵敏的化学发光检测；同时四通道成像，检测更高效。 Azure 多功能荧光凝胶成像系统

近日，新华社“走进中国新科技”系列专题对北京航空航天大学生物与医学工程学院樊瑜波、李德玉、汪待发联合团队所研发的近红外脑功能成像技术进行了深入报道今天，带大家走近联合团队中的汪待发副教授踏足“脑功能疾病诊疗”科技前沿汪 待 发北京航空航天大学生物与医学工程学院副教授、博士生导师从事近红外脑功能成像、脑机接口、脑功能评价、神经调控等方面研究已有20余载，作为课题组长承担国家重大科学仪器研制项目1项、国家重点研发计划1项；主持国家自然科学基金面上、青年等基金课题。发表SCI论文40余篇，申请发明专利数十项。致力于近红外脑功能成像领域的研究、研发、产业化与临床应用，研发装备已在包括301医院、宣武医院、上海华山医院、清华大学等400余家单位示范应用；支撑在Human Behaviour、Journal of Cleaner Production、NeuroImage等杂志发表SCI论文120余篇。攻克世界难题研发“戴在头上的功能核磁”大脑是人类最复杂神秘的器官，思想的萌生之地，生命的承载中枢。了解大脑的功能和运行机制，可以揭示人类学习、智慧、发育的诸多奥秘，也是治疗中风、阿尔茨海默症、抑郁症、精神分裂症等重大脑疾病的基础。人类对大脑运行机制的不断探索和深刻理解，更为新一代类脑人工智能技术的飞速发展，提供了关键的生物学理论基础。自然状态下大脑活动的高分辨成像是世界难题。目前，主流的脑功能成像方法包括功能核磁共振（fMRI）、核素成像（PET）、脑电（EEG）、近红外脑功能成像（fNIRS）等。然而，大型脑功能成像系统包括fMRI、PET体积庞大，并且患者不能有头动，不适合于自然情景；EEG相对轻便，然而其空间分辨率低，并且对于头动、电磁的干扰均非常敏感。近红外脑功能成像，为自然状态下的高分辨脑成像带来了新型技术平台，亦被称为“戴在头上的功能核磁”。它和fMRI一样，探测的是大脑氧代谢的载体（血红蛋白）的浓度变化。由于采用的光学手段，它空间分辨率高（1-3cm）、适合于各种自然状态，可以一边运动一边检测、一边说话一边检测、一边治疗一边检测，为中国上亿的脑功能障碍疾病患者的诊断、疗效评价、疗效预测、用药/干预/康复方案的指导等提供了创新性手段，这包括脑卒中神经康复、精神疾病、儿童发育障碍（孤独症谱系障碍等）及神经退行性疾病（阿尔茨海默病等）等。近红外脑功能成像原理然而，高端脑影像设备的关键技术长期被发达国家垄断。例如近红外脑功能成像设备，长期被美日等垄断，单价在数百万，但却不能解决亚洲人有黑色头发覆盖区域（顶叶、枕叶等）成像的难题，限制了脑功能检查和研究的开展。汪待发副教授，是近红外脑功能成像技术第三代的践行者。2010年博士毕业后，他来到北京航空航天大学生物与医学工程学院任教。当时，北航生医学院刚刚建院不久，立意高远，把学院科研发展聚焦在解决国家重大需求牵引的医工科学和技术上。汪待发扎根北航，攻坚近红外脑功能成像领域的难题。通过自己多年如一日的努力，以及与包括樊瑜波、李德玉等北航的血流动力学分析、高精密传感专家的不断研讨和思想碰撞，经历数百次的试验、挫折和迭代验证，他终于突破了近红外超微光探测技术，攻克了亚洲人有黑色头发的脑区（顶叶、枕叶等）的快速精准成像的世界难题。汪待发团队fNIRS产品覆盖的行业应用2016年初，依托北航校地合作平台孵化，汪待发创立了慧创医疗，立志要克服成果转化这个陌生领域的重重困难，坚定地把科研成果落实在祖国的大地上。依托科技风险投资的资金支持，汪待发领导的慧创团队与北航联合团队开展合作，充分发挥产学研合作优势，2019年研发推出了世界上首个获得医疗器械注册证的、超100通道的近红外脑功能成像装置，突破性地实现了全脑成像，实现了中国近红外脑功能成像领域自主知识产权的开创性进展。世界上首个获得医疗器械注册证的、超100通道的近红外脑功能成像装置在此基础上，将超微光技术进一步数字化，汪待发带领团队研发了世界首台获医疗器械证的便携式近红外脑功能成像设备。其平板电脑大小的身形，却具备领先于进口台式设备的成像性能，让临床和科研专家惊叹，赢得了广泛的认可。世界首台获医疗器械证的便携式近红外脑功能成像设备目前，汪待发团队所转化的近红外脑功能成像系列产品及技术，已在301、北京协和、上海华山、四川华西、清华大学、北京师范大学、香港理工大学等800余家一流临床及科研单位示范应用，开展临床检查和科学研究，并已支撑专家在以Nature Human Behaviour为代表的顶级期刊上，发表了SCI论文180余篇，在国内外形成了广泛影响。在北航原始创新的加持下，慧创医疗作为唯一一家企业起草单位，与国家药监局合作，制定了中国首个近红外脑功能成像强制性国家标准。同时，近红外脑功能成像产品NirScan，因其“高精尖”装备+原创+领先的综合属性，获评江苏省首台（套）重大装备。近红外脑成像设备支持用户发表的高水平SCI论文致力于科技成果转化解决临床应用痛点为推动近红外脑功能成像更好地解决临床痛点需求，作为医工专家，汪待发积极把自己变成“最懂临床需求的科学家”。目前，他担任了中国康复医学会脑功能检测与调控康复专业委员会常务委员、第二届中国妇幼健康研究会婴幼儿心理健康专业委员会常务委员、中国康复医学会阿尔茨海默病与认知障碍康复专业委员会青年组副组长，并担任了浙江大学医学院附属精神卫生中心（杭州市第七人民医院）特聘专家、国家药品监督管理局医疗器械技术审评中心外聘专家。作为fNIRS领域TOP科学家，他每年在全国各地完成约30余场高质量的学术讲座，与临床专家深入交流，积极推动近红外脑功能成像在临床各个领域的广泛应用。同时，在樊瑜波教授的鼓励下，依托国家医学攻关产教融合平台(医工结合)，汪待发所带领的团队，仅2023年就开展了多元化多层次的脑科学领域相关培训近20次，合计邀请了近70位脑科学及相关领域专家，合计线下培训人员超600人，线上培训超8000人。2021年，汪待发与国内顶级医院的临床专家一起，撰写了中国首个近红外脑功能成像专家共识，为该技术在临床的快速应用和发展做出了积极推动。2022年底，北航樊瑜波、李德玉、汪待发联合团队的“近红外脑功能成像系统开发及临床应用”成果获得了中国生物医学工程学会最高奖项——“黄家驷”生物医学工程奖。这一奖项的获得，体现了中国生物医学工程行业对北航近红外脑功能成像技术和系统成果的充分肯定。近红外脑功能成像系统荣获“黄家驷”生物医学工程奖证书近年来，在近红外脑功能成像技术的基础上，在国家重点研发计划的牵引下，汪待发团队瞄准了另一个脑科学世界级难题“阿尔茨海默症（老年痴呆症）治疗”。团队目前在阿尔兹海默症治疗方面已取得突破性进展，其研发的“近红外光脑功能治疗仪”目前已获批国家药品监督管理局（NMPA）医疗器械绿色通道（创新医疗器械设置特别审批通道）。这是国家药监局为具备重大创新的医疗器械开辟的一条审查极为严格的注册证快速申请通道。从2014年国家药监局正式颁布《创新医疗器械特别审批程序（试行）》的近十年来，仅批准了300余项。目前，在国家科技成果转化引导基金的支持下，团队正在和临床专家们合作，开展阿尔茨海默症治疗产品的临床试验。托举学子梦想培育医工行业未来作为年轻科学家，在承接前辈科学家的教诲和精神的同时，汪待发也已成长为带领年轻学子的领头人。汪待发一直将人才培养与国家需求紧密结合，以人民群众的生命健康为牵引，鼓励学生们“能人所不能，坚持解决临床核心痛点，做世界领先的高水平研究”，从临床实际中挖掘科学问题，并将研究成果应用到临床实际中去，扎扎实实地把科研写在祖国的大地上。汪代发与课题组硕博士生合影“要在学生最有梦想的时候好好引导他们，他们是祖国与行业的明天，要让他们放飞思想，追逐科技创新的梦想。”汪待发在科研之余还担任北航冯如书院本科生导师。作为导师，他悉心指导硕士、博士研究生近20人，攻坚脑功能疾病诊疗的难题。他将科研及转化的经验融入课堂教学，近三年担任《生理信号检测与处理实验》的负责人，不断完善课程建设，引导学生主动思考、发现问题、解决问题；作为《医学成像系统》和《生物医学成像技术》的主讲老师，带领学生认识行业内的新技术新成果，培养具有前沿视野的行业接班人。将科研与国家的重大需求做贴合攻坚中国脑功能疾病难题做世界领先的高端脑功能疾病诊疗装备和汪待发副教授一样在北航奋斗的广大教师们一直在脚踏实地、仰望星空潜心科研、矢志创新在建设科技强国人才强国的新征途中上下求索，砥砺前行！

近日，中国科学院深圳先进技术研究院（简称“深圳先进院”）成功研发国内首台高清晰磁共振兼容人脑PET功能成像仪器（命名为“SIAT bPET”），实现了我国在高端磁兼容脑PET成像仪器研发方面零的突破。“通常，PET成像仪器由于探测器的深度不确定效应，空间分辨率会随着偏离成像视野中心而变差，严重影响成像精度。”深圳先进院医工所劳特伯生物医学成像研究中心研究员杨永峰表示，他们团队研发了高三维分辨率双端读出探测器，使得该大口径成像系统达到14%的中心效率（350-750 keV能量窗），和整个成像视野好于1.4 mm的空间分辨率，两项性能指标都处于国际领先水平。 杨永峰介绍道，与国外商业磁兼容脑PET成像仪器相比，SIAT bPET的效率提高了近2倍（从7.2%到14%），平均体分辨率提高了30倍以上（从约64mm3到2mm3）。同时，SIAT bPET采用了创新的电子学和磁兼容设计，使得磁共振成像对PET成像的影响几乎可以忽略不计，PET成像对磁共振成像图像信噪比的影响小于5%，满足同时开展PET/MRI成像的尖端科研需求。 据了解，PET和MRI都是脑科学研究和脑疾病诊断的重要工具，PET的高灵敏度、高定量精度功能代谢成像和MRI的高空间分辨率、高软组织对比度解剖结构成像高度互补，PET和MRI还可以相互辅助，进一步提升各自的脑神经成像能力。PET分子成像通过测量大脑的血流、葡萄糖和氧的代谢、蛋白质的生成、药物的分布和神经递质的动力学等，探索不同脑区的功能，确定病变脑区的功能演变，对于脑疾病干预治疗策略和新药物探索具有重要意义。 “不过，目前市场上并没有高性能脑PET成像仪器。”杨永峰说，与美国脑计划项目正在资助研发的多个高性能脑PET成像仪器相比，SIAT bPET的空间分辨率和效率也处于先进水平。“高空间分辨率使得研究大脑的细微焦点脑功能区和小的核团成为可能，还可以通过降低部分容积效应来提高脑PET成像研究的定量精度；高效率除了通过提高脑PET图像的信噪来提高研究的定量精度，也为高精度研究神经递质活动和其他动态脑生化与功能活动奠定基础。” 2022年，团队成员邝忠华在国际核医学和分子影像年会与IEEE医学成像会议上口头报告了该研究成果，随即引起了广泛的国际关注。同时，该仪器也为开展基于PET功能成像的脑科学研究、老年性痴呆等疾病的早期定量诊断研究和新药开发提供了一台重要的新工具。 据悉，相关研究由基金委国家重大科研仪器研制、深圳市孔雀团队和中国科学院仪器研制团队等项目资助。 深圳先进院研制的SIAT bPET探测器系统和脑成像仪器照片SIAT bPET获得的Derenzo模体图、人脑FDG代谢图和兔子NaF骨扫描图SIAT bPET和联影uMR790 3T磁共振成像系统上同时获得的人脑PET/MRI图像关于PET：正电子发射断层扫描（PET）是一种核成像技术（也称为分子成像），可以显示体内代谢过程。PET成像的基础是该技术检测由正电子发射放射性核素（也称为放射性药物，放射性核素或放射性示踪剂）间接发射的γ射线对。将示踪剂注入生物活性分子的静脉中，通常是用于细胞能量的糖。PET系统灵敏的探测器捕获身体内部的伽马射线辐射，并使用软件绘制三角测量排放源，创建体内示踪剂浓度的三维计算机断层扫描图像。目前主要的PET系统制造商包括GE Healthcare，Philips Healthcare，Siemens Healthcare和Toshiba。PET/MRI系统的供应商包括GE，飞利浦和西门子。SPECT供应商包括通用电气，飞利浦，西门子和Digirad公司。

2021年5月，多功能高分辨率磁光克尔显微成像系统在清华大学顺利完成安装和调试，并获得用户的高度认可。该系统是由北京航空航天大学集成电路学院赵巍胜教授指导，张学莹老师带领团队根据多年积累的磁畴动力学实验技巧和 新的磁学及自旋电子学领域的热点课题研究需求设计的，也是Quantum Design中国与致真精密仪器（青岛）有限公司合作推出后在国内完成的套安装和验收。 致真精密仪器（青岛）有限公司工程师与用户的现场合影 安装精彩瞬间相比于传统的磁光克尔显微镜，该系统除了拥有高达300 nm的纵向和向克尔成像（分别对应面内和垂直各向异性样品磁畴测量），还增加了灵活的磁场探针台及面内旋转的磁场和高度智能化的软件控制系统。其中磁场探针台可以同时施加面内和垂直的磁场，通过智能控制系统，能够让用户利用软件定义电、磁等多种想要的波形，一键触发后，在样品上可同步施加垂直/面内磁场、电流脉冲、微波信号，进行磁光克尔成像及微区磁滞回线提取、局部饱和磁化强度Ms表征、局部各项异性能K的表征、海森堡交换作用常数Aex，Dzyaloshinskii-Moriya作用的表征等，在磁性薄膜材料和自旋电子器件动力学分析领域有着突出的优势。这套多功能高分辨率磁光克尔显微成像系统历经5年多的研发历程，在北航集成电路学院、北航青岛研究院的支持下，经过了3轮迭代和试用，在致真精密仪器（青岛）有限公司团队进行工程化之后，形成了性能稳定，功能多样，多场景适配改装方便的系统。该产品还获得了青岛市市长杯创新创业大赛一等奖。北航团队在该设备的强大功能支撑下，在DMI测量[1]、自旋轨道矩（SOT）效应研究[2]、磁畴壁动力学[3-4]、磁性材料和自旋电子器件研究[5]等方面，取得了丰富的成果。同时，该设备还可用于永磁材料和硅钢等软磁材料的磁畴分析等。该设备的成功落户标志着国产商用磁光克尔显微镜领域的长期空白得以弥补。作为北航集成电路学院工艺与装备系孵化的公司，致真精密仪器（青岛）有限公司传承了北航文化，响应在高端科研设备方面的需求，与时俱进，精益求精，敢于啃硬骨头，做高品质高可靠性产品。同时，作为本土企业，致真精密仪器会始终与用户保持良好沟通，紧密追踪前沿热点，以用户的需求和科学发展方向为指引，将 新的测试技术融入到产品中去，为新老用户持续做好服务，支持中国甚至全球更多的科研者的科学探索。目前，该系统已经更新至三代，感谢所有提出过建议的老师和同学们，也欢迎大家继续提供宝贵的意见！在此，特别感谢清华大学的老师对我们的信任与支持，祝他们科研顺利，硕果累累！目前，这款多功能高分辨率磁光克尔显微成像系统已经获得了清华大学、中国科学院物理研究所、北京工业大学、上海科技大学等客户多套订单。 产品基本参数： ☛ 向和纵向克尔成像分辨率可达300 nm；☛ 配置二维磁场探针台，面内磁场 高达1 T，垂直磁场 高达0.3 T（配置磁场增强模块后可达1.5 T）；☛ 快速磁场选件磁场反应速度可达1 μs；☛ 可根据需要选配直流/ 高频探针座及探针；☛ 可选配二次谐波、铁磁共振等输运测试；☛配置智能控制和图像处理系统，可同时施加面内磁场、垂直磁场和电学信号同步观测磁畴翻转；☛ 4K~800K，80K~500K 变温选件可选。 样机体验：目前，致真精密仪器（青岛）有限公司可对相关领域感兴趣的科学工作者提供测样体验，欢迎感兴趣的老师或同学通过拨打电话010-85120280或发送邮件至info@qd-china.com体验磁光克尔显微成像全新技术！ 参考文献：[1]. Cao, A. et al. Tuning the Dzyaloshinskii–Moriya interaction in Pt/Co/MgO heterostructures through the MgO thickness. Nanoscale 10, 12062–12067 (2018).[2]. Zhao, X. et al. Ultra-efficient spin–orbit torque induced magnetic switching in W/CoFeB/MgO structures. Nanotechnology 30, 335707 (2019).[3]. Zhang, X. et al. Low Spin Polarization in Heavy-Metal–Ferromagnet Structures Detected Through Domain-Wall Motion by Synchronized Magnetic Field and Current. Phys. Rev. Appl. 11, 054041 (2019).[4]. Zhang, Y. et al. Domain-Wall Motion Driven by Laplace Pressure in CoFeB/MgO Nanodots with Perpendicular Anisotropy. Phys. Rev. Appl. 9, 064027 (2018).[5]. Zhang, X. et al. Spin‐Torque Memristors Based on Perpendicular Magnetic Tunnel Junctions for Neuromorphic Computing. AdvancedScience 8, 2004645 (2021).

p 　　6月20日至21日，国家自然科学基金委员会在京对中国科学院化学研究所承担的重大仪器研制项目“高分辨多功能化学成像系统”进行了结题验收。国家自然科学基金委员会相关负责人、中科院条件保障与财务局相关负责人、项目验收专家组、项目监理组、化学所相关人员、项目组全体成员等70余人参加了项目验收会。项目验收专家组由包括仪器测试组、财务验收组、档案验收组等在内的18位专家组成，中科院院士柴之芳担任验收专家组组长。结题验收会由国家自然科学基金委员会化学学部常务副主任陈拥军主持。 /p p 　　国家自然科学基金委员会副主任姚建年在发言中指出，重大仪器研制项目的设立符合国家创新驱动发展战略的需求，仪器创新是科研创新的源头。陈拥军介绍了“高分辨多功能化学成像系统”项目的立项过程，并对验收工作提出了具体要求。中科院条件保障与财务局副局长曹凝介绍了中科院的监理制度和监理情况，对基金委长期以来对中科院仪器创新工作的支持表示感谢。 /p p 　　项目负责人、中科院院士万立骏对“高分辨多功能化学成像系统”项目的完成情况进行了详细汇报。该系统包括超分辨光学STED成像模块、CARS成像模块、AFM成像模块、共聚焦激发的MALDI-MS成像模块、SIMS质谱成像模块等，能够在各模块单独工作的基础上，实现各模块之间的联用成像，在纳米尺度和分子水平对复杂体系界面结构进行形貌和化学组成表征。仪器测试专家组在验收会前对仪器进行了现场严格测试，全部技术指标达到或优于任务书预定的要求。利用研制的化学成像系统，项目组在能源材料和生物体系的表界面结构与功能等领域取得了系列研究成果，申请国际国内发明专利40余件，授权国际专利4件，国内专利14件，发表了一批高水平论文。在项目执行过程中，项目组在技术人才培养方面探索出了新的机制，形成了一支有特色的多学科交叉的科学仪器研制团队。 /p p 　　验收专家组现场查看了研制系统的运行情况，并对财务和档案进行了验收。验收专家组听取了监理报告、仪器测试报告、档案验收报告和财务验收报告。通过现场考察和听取汇报，验收专家组认为，该项目完成了实施方案规定的研制任务，达到了项目预期目标，一致同意项目通过验收。 /p p style=" text-align: center " img src=" http://img1.17img.cn/17img/images/201706/insimg/d317e9ca-86a6-4da7-9af0-f79f022f8745.jpg" title=" iVGd-fyhskrp7666782.jpg" / 　　 /p p style=" text-align: center " 验收会主会场 br/ /p p br/ /p

p 　　6月20日至21日，国家自然科学基金委员会在京对中国科学院化学研究所承担的重大仪器研制项目“高分辨多功能化学成像系统”进行了结题验收。国家自然科学基金委员会相关负责人、中科院条件保障与财务局相关负责人、项目验收专家组、项目监理组、化学所相关人员、项目组全体成员等70余人参加了项目验收会。项目验收专家组由包括仪器测试组、财务验收组、档案验收组等在内的18位专家组成，中科院院士柴之芳担任验收专家组组长。结题验收会由国家自然科学基金委员会化学学部常务副主任陈拥军主持。 /p p 　　国家自然科学基金委员会副主任姚建年在发言中指出，重大仪器研制项目的设立符合国家创新驱动发展战略的需求，仪器创新是科研创新的源头。陈拥军介绍了“高分辨多功能化学成像系统”项目的立项过程，并对验收工作提出了具体要求。中科院条件保障与财务局副局长曹凝介绍了中科院的监理制度和监理情况，对基金委长期以来对中科院仪器创新工作的支持表示感谢。 /p p 　　项目负责人、中科院院士万立骏对“高分辨多功能化学成像系统”项目的完成情况进行了详细汇报。该系统包括超分辨光学STED成像模块、CARS成像模块、AFM成像模块、共聚焦激发的MALDI-MS成像模块、SIMS质谱成像模块等，能够在各模块单独工作的基础上，实现各模块之间的联用成像，在纳米尺度和分子水平对复杂体系界面结构进行形貌和化学组成表征。仪器测试专家组在验收会前对仪器进行了现场严格测试，全部技术指标达到或优于任务书预定的要求。利用研制的化学成像系统，项目组在能源材料和生物体系的表界面结构与功能等领域取得了系列研究成果，申请国际国内发明专利40余件，授权国际专利4件，国内专利14件，发表了一批高水平论文。在项目执行过程中，项目组在技术人才培养方面探索出了新的机制，形成了一支有特色的多学科交叉的科学仪器研制团队。 /p p 　　验收专家组现场查看了研制系统的运行情况，并对财务和档案进行了验收。验收专家组听取了监理报告、仪器测试报告、档案验收报告和财务验收报告。通过现场考察和听取汇报，验收专家组认为，该项目完成了实施方案规定的研制任务，达到了项目预期目标，一致同意项目通过验收。 /p

磁畴是铁磁体材料在自发磁化的过程中，为降低静磁能而产生分化的方向各异的小型磁化区域。它的研究可将材料的基本物理性质、宏观性质和应用联系起来。近年来，由于材料的日益完善和器件的小型化，人们对磁畴分析的兴趣与日俱增。目前市面上主要的磁畴观测设备有磁光克尔显微镜、磁力显微镜、洛伦兹电镜、以及近兴起的NV色心超分辨磁学显微镜等，其中，磁光克尔显微镜可以灵活的结合外加磁场、电流及温度环境等来对材料进行面内、面外的动态磁畴观测，成为目前常用的磁畴观测设备，可用于多种磁性材料的研究，如铁磁或亚铁磁薄膜、钕铁硼等硬磁材料、硅钢等软磁材料。 2020年11月，Quantum Design中国与致真精密仪器（青岛）有限公司签署了中国区战略合作协议，合作推出多功能高分辨率磁光克尔显微成像系统。通过此次战略合作，Quantum Design中国希望能够为磁学及自旋电子学等领域的研究提供更多的可能。图1 多功能高分辨率磁光克尔显微成像系统 多功能高分辨率磁光克尔显微成像系统由北京航空航天大学集成电路学院张学莹老师带领团队，根据多年的磁畴动力学实验技巧积累和新的磁学及自旋电子学领域的热点课题研究需求研发。它采用先进的点阵LED光源技术，能够在不切换机械结构的情况下，同时进行向和纵向克尔成像，不仅能同时检测样品垂直方向和面内方向的磁性，成像分辨率还能够达到270 nm，逼近光学衍射限。与传统的磁光克尔显微镜相比，多功能高分辨率磁光克尔显微成像系统配置了多功能磁铁探针台，能够在保证450 nm高分辨率的前提下，向被测样品同时施加面磁场、垂直磁场、电流和微波信号。 此外，多功能高分辨率磁光克尔显微成像系统拥有专门的智能控制系统，用户界面友好，无需复杂设置，一键触发既能实现多维度磁场、电学信号与克尔图像的同步操控。该系统的另一亮点是配置了反应速度高达1 μs的超快磁场，为微米器件中磁畴的产生、磁畴的高速运动捕捉等提供了可能。 张学莹老师师从北航赵巍胜教授和法国巴黎萨克雷大学Nicolas Vernier教授，从2015年开始研究磁光克尔成像技术和磁畴动力学，其有关磁性材料性质的论文获得北京航空航天大学博士学位论文。经过3年潜心研究，该团队于2018年完成了台克尔显微镜样机的集成，并创立致真精密仪器（青岛）有限公司。至2020年初，在北航青岛研究院和北航集成电路学院经过两轮迭代和打磨，已经完成了产品的稳定性验证，目前，该设备已经被清华大学、中科院物理所、北京工业大学等多家单位采购。 产品磁畴成像照片案例图2 CoFeB(1.3 nm)/W(0.2)/CoFeB(0.5)薄膜中的迷宫畴图3 斯格明子磁畴观测 多重信号的叠加，能够满足客户多种前沿课题的实验需求面内磁场和垂直磁场的叠加可以进行Dzyaloshinskii-Moriya作用（DMI）的测试[1,2]图4 样品Pt(4 nm)/Co(1 nm)/MgO(t nm)/Pt(4 nm)DMI作用测量[1] 自旋轨道矩（spin-orbit torque,简称SOT）是近年来发展起来的新一代电流驱动磁化翻转技术，如何更好的表征SOT翻转，在当今自旋电子学领域具有重要的理论和应用价值。 多功能高分辨率磁光克尔显微成像系统配置的面内磁场和电学测试系统，不但可以实现这个过程的电学测试，还可以利用相机与信号采集卡同步的功能，逐点解析翻转曲线对应的磁畴状态 [3,4]。图5 面内磁场和电流的叠加用于sot驱动的磁性变化过程研究 在某些材料中，无法观测到纯电流驱动的磁畴壁运动。这时，可以利用多功能高分辨率磁光克尔显微成像系统微秒别的超快磁场脉冲与电流同步，观测垂直磁场与电流共同驱动的畴壁运动，从而解析多种物理效应，如重金属/ 铁磁体系的自旋化率由于自旋散射降低的效应 [5]。图6 垂直磁场和电流的叠加可用于观测单磁场或者电流无法驱动的磁性动力学过程 克尔成像下磁场和微波的叠加则能够为自旋波和磁畴壁的相互作用研究提供可能[6]。图7 自旋波驱动的磁畴壁运动[6] 多功能高分辨率磁光克尔显微成像系统还可进行多种磁性参数的微区测量局部饱和磁化强度Ms表征[7]由于偶作用，磁畴壁在靠近时会相互排斥。通过观察不同磁场下磁畴壁的距离，可以提取局部区域的饱和磁化强度Ms。此方法由巴黎- 萨克雷大学Nicolas Vernier 教授（致真技术顾问）在2014 年先提出并验证，与VSM测量结果得到良好吻合。图8 局部饱和磁化强度Ms表征及与其他测试方法Ms结果对比 海森堡交换作用刚度[8]采用系统的磁场“自定义波形”功能，将样品震荡退磁，再将得到的迷宫畴图片进行傅里叶变换，能够得知磁畴宽度，从而提取海森堡交换作用刚度Aex。图9 海森堡交换作用刚度提取 自旋电子薄膜质量的表征、自旋电子器件的损坏检测等[9]图10 磁性薄膜质量检测 除此之外，该系统还开发了性价比超高的变温系统。针对永磁材料研究的用户，开发了能够兼容克尔成像的高温强磁场模块。针对硅钢等软磁材料研究用户，开发了大视野面内克尔显微镜。 动态磁畴成像案例图11 cofeb薄膜动态磁畴图12 sot磁场+电流驱动磁畴翻转图13 钕铁硼永磁动态磁畴观测图14 磁性材料内钉扎点的观测，可与巴克豪森噪声同步匹配 产品基本参数✔ 向和纵向克尔成像分辨率可达300 nm；✔ 配置二维磁场探针台，面内磁场高达1 t，垂直磁场高达0.3 t（配置磁场增强模块后可达1.5 t）；✔ 快速磁场选件磁场反应速度可达1 μs；✔ 可根据需要选配直流/ 高频探针座及探针；✔ 可选配二次谐波、铁磁共振等输运测试；✔ 配置智能控制和图像处理系统，可同时施加面内磁场、垂直磁场和电学信号同步观测磁畴翻转；✔ 4k~800k，80k~500k 变温选件可选。 小结多功能高分辨率磁光克尔显微成像系统除了拥有超高分辨的动态磁畴观测能力外，还能结合多功能磁场探针台提供的外加电流、面内/面外磁场等对多种磁学参数进行提取。 样机体验目前，致真精密仪器（青岛）有限公司可对相关领域感兴趣的科学工作者提供了测样体验，欢迎感兴趣的老师或同学拨打电话010-85120280或发送邮件至info@qd-china.com体验磁光克尔显微成像全新技术！ 参考文献[1] A. Cao et al., Nanoscale 10, 12062 (2018).[2] A. Cao et al., Nanotechnology 31, 155705 (2020).[3] X. Zhao et al., Appl. Phys. Lett. 116, 242401 (2020).[4] G. Wang et al., IEEE Trans. Circuits Syst. I Regul. Pap. 66, 215 (2019).[5] X. Zhang et al., Phys. Rev. Appl. 11, 054041 (2019).[6] J. Han et al., Science (80-. ). 366, 1121 (2019).[7] N. Vernier et al., Appl. Phys. Lett. 104, 122404 (2014).[8] M. Yamanouchi et al., IEEE Magn. Lett. 2, 3000304 (2011).[9] Y. Zhang et al., Phys. Rev. Appl. 9, 064027 (2018).

Cytation™ 7 细胞成像多功能检测系统具有独特的专利设计，它将数字化的正置和倒置显微成像技术与传统的多模式微孔板检测技术结合于一体，支持透射光成像模式和反射光成像模式，集高通量、自动化、多模式为一套系统中，进一步拓宽了Cytation系列产品在细胞成像领域的应用范围，为生命科学领域提供有力的研究工具。产品特点1. 机载多种模式的检测方式，其中包括正置和倒置显微成像光路，从而可以实现广泛的透射和反射光应用，支持明场、彩色明场、荧光场的成像模式，适用于常规细胞学、组织学等不同样品成像，也可以用于于植物和动物样品成像。2、 一体化避光设计，体积小巧，同时具有专利的4-Zone温度控制功能，良好的温控均一性，能有效避免边缘效应和凝结水蒸气的产生。可选Peltier冷却模块，支持气体控制和自动加样器的扩展，适合活细胞检测。3、正置成像模块可以快速实现ELISpot、HE染色、明胶图片拍摄、克隆计数等应用。4、全功能酶标检测模块采用第四代光栅技术，满足吸收光、荧光、发光检测需求，可调带宽功能可以兼顾不同荧光染料的灵敏度和特异性，实现无与伦比的微孔板检测性能。5、独特的Hit-pick功能专业用于高通量筛选实验，可以实现快速的高通量筛选检测并减少数据的存贮空间。6、Gen5™ 软件具有易用性和强大的处理分析功能7、 广泛的应用空间 创新点：Cytation 7 细胞成像微孔板检测系统创新的整合了全自动数字正置和倒置宽视场显微镜以及便捷的多功能微孔板测读系统，三种功能模块采用专利设计集成于一套小巧的系统之中。倒置显微成像模块可以完成1.25× 至60× 物镜的荧光场，明场和彩色明场成像，应用范围非常广泛。正置显微镜可以完成反射光和透射光明场成像，可以进一步拓展产品的应用范围，创新的将正倒置成像系统整合在一台仪器上可以极大的满足成像用户的实验需求。 BioTek Cytation 7 细胞成像多功能检测系统

了解ibright™ 智能成像系统——蛋白质免疫印迹成像的最新进展。新品发布——ibright智能成像系统全新invitrogen™ ibright™ 智能成像系统重磅上市！通过强劲的系统配置、先进的自动化功能和友好的用户界面，ibright成像系统可显著提升蛋白免疫印迹实验体验，助您轻松获得理想结果。灵活多样的成像方案——适用于多色荧光western blot印迹、化学发光western blot印迹、蛋白凝胶和核酸凝胶成像一键式优化曝光——smart exposure™ 智能曝光技术与高灵敏910万像素冷ccd相机的结合，具备强劲的成像性能简洁流畅的操作体验——直观友好的界面设计结合高度自动化功能，帮助各种经验水平的研究人员快速上手多重成像能力——实现多达4色荧光western blot的多重成像，拓展了在单块印迹上同时检测多种蛋白质的能力小体积，大视野——紧凑的一体化设计与大尺寸成像视野兼具，可一次采集多达4块小型印迹膜或凝胶图像即刻加速您的蛋白质免疫印迹研究进程，请点击thermofisher.com/ibright

项目概况 受福州大学委托，福建顺恒工程项目管理有限公司对[3500]FJSH[GK]2022011、福州大学原位电化学电池多功能光谱快速成像系统采购项目组织公开招标，现欢迎国内合格的供应商前来参加。 福州大学原位电化学电池多功能光谱快速成像系统采购项目的潜在投标人应在福建省政府采购网(zfcg.czt.fujian.gov.cn)免费申请账号在福建省政府采购网上公开信息系统按项目获取采购文件，并于2022-05-30 09:00（北京时间）前递交投标文件。一、项目基本情况 项目编号：[3500]FJSH[GK]2022011 项目名称：福州大学原位电化学电池多功能光谱快速成像系统采购项目 采购方式：公开招标 预算金额：1490000元 包1： 采购包预算金额：1490000元 投标保证金：14900元 采购需求：（包括但不限于标的的名称、数量、简要技术需求或服务要求等）品目号品目编码及品目名称采购标的数量（单位）允许进口简要需求或要求品目预算（元）1-1A021099-其他仪器仪表原位电化学电池多功能光谱快速成像系统1（套）是详见招标文件1490000 合同履行期限： 自合同生效之日起至合同约定的合同义务履行完毕 本采购包：不接受联合体投标二、申请人的资格要求： 1.满足《中华人民共和国政府采购法》第二十二条规定； 2.本项目的特定资格要求： 包1（如项目接受联合体投标，对联合体应提出相关资格要求；如属于特定行业项目,供应商应当具备特定行业法定准入要求。) 三、采购项目需要落实的政府采购政策 （1）财政部、工业和信息化部《关于印发〈政府采购促进中小企业发展管理办法〉的通知》财库[2020]46号文件规定（适用于本项目）。（2）财政部、司法部联合印发《关于政府采购支持监狱企业发展有关问题的通知》（财库[2014]68号）文件规定（适用于本项目）。（3）财政部、民政部、中国残疾人联合会印发的《三部门联合发布关于促进残疾人就业政府采购政策的通知》财库〔2017〕141号文件规定（适用于本项目）。（4）节能产品、环境标志产品（适用于本项目）（5）进口产品：根据财政部《政府采购进口产品管理办法》（财库[2007]119号）及《关于政府采购进口产品管理有关问题的通知》(财办库［2008］248号)要求，本次采购合同包1允许采购进口产品。四、获取招标文件 时间：2022-05-05 18:35至2022-05-20 23:59（提供期限自本公告发布之日起不得少于5个工作日），每天上午00:00:00至11:59:59，下午12:00:00至23:59:59（北京时间，法定节假日除外) 地点：招标文件随同本项目招标公告一并发布；投标人应先在福建省政府采购网(zfcg.czt.fujian.gov.cn)免费申请账号在福建省政府采购网上公开信息系统按项目下载招标文件(请根据项目所在地，登录对应的(省本级/市级/区县)）福建省政府采购网上公开信息系统操作)，否则投标将被拒绝。 方式：在线获取 售价：免费五、提交投标文件截止时间、开标时间和地点 2022-05-30 09:00（北京时间）（自招标文件开始发出之日起至投标人提交投标文件截止之日止，不得少于20日） 地点：福州市本级鼓楼区西洪路363号4层、5层 - 1号开标室六、公告期限 自本公告发布之日起5个工作日。七、其他补充事宜 详见招标文件八、对本次招标提出询问，请按以下方式联系。 1.采购人信息 名 称：福州大学 地 址：福建省福州市福州地区大学新区学园路2号 联系方式：0591-22865917 2.采购代理机构信息（如有） 名 称：福建顺恒工程项目管理有限公司 地　　址：福州市鼓楼区西洪路363号4层、5层 联系方式：13859088048 3.项目联系方式 项目联系人：晏静、王桂香 电　　 话：13859088048 网址：zfcg.czt.fujian.gov.cn 开户名：福建顺恒工程项目管理有限公司 福建顺恒工程项目管理有限公司 2022-05-05

一、项目基本情况项目编号：GPDIZB-2022-A02ZJ094项目名称：广东医科大学购置多功能化学发光成像系统等设备一批采购方式：公开招标预算金额：1,500,000.00元采购需求：合同包1(多功能化学发光成像系统等设备):合同包预算金额：1,500,000.00元品目号品目名称采购标的数量（单位）技术规格、参数及要求品目预算(元)最高限价(元)1-1其他专用仪器仪表多功能化学发光成像系统等仪器设备一批1(批)详见采购文件1,500,000.00-本合同包不接受联合体投标合同履行期限：采购合同签订之日起30个工作日内完成交货、安装调试。二、申请人的资格要求：1.投标供应商应具备《政府采购法》第二十二条规定的条件，提供下列材料：1）具有独立承担民事责任的能力：在中华人民共和国境内注册的法人或其他组织或自然人， 投标（响应）时提交有效的营业执照（或事业法人登记证或身份证等相关证明） 副本复印件。分支机构投标的，须提供总公司和分公司营业执照副本复印件，总公司出具给分支机构的授权书。2）有依法缴纳税收和社会保障资金的良好记录：提供投标截止日前6个月内任意1个月依法缴纳税收和社会保障资金的相关材料。 如依法免税或不需要缴纳社会保障资金的， 提供相应证明材料。3）具有良好的商业信誉和健全的财务会计制度：供应商必须具有良好的商业信誉和健全的财务会计制度（提供2021年度财务状况报告或基本开户行出具的资信证明） 。4）履行合同所必需的设备和专业技术能力：按投标（响应）文件格式填报设备及专业技术能力情况。5）参加采购活动前3年内，在经营活动中没有重大违法记录：参照投标（报价）函相关承诺格式内容。 重大违法记录，是指供应商因违法经营受到刑事处罚或者责令停产停业、吊销许可证或者执照、较大数额罚款等行政处罚。（根据财库〔2022〕3号文，“较大数额罚款”认定为200万元以上的罚款，法律、行政法规以及国务院有关部门明确规定相关领域“较大数额罚款”标准高于200万元的，从其规定）2.落实政府采购政策需满足的资格要求： 无。3.本项目的特定资格要求：合同包1(多功能化学发光成像系统等设备)特定资格要求如下:(1)供应商未被列入“信用中国”网站(www.creditchina.gov.cn)“记录失信被执行人或重大税收违法案件当事人名单或政府采购严重违法失信行为”记录名单；不处于中国政府采购网(www.ccgp.gov.cn)“政府采购严重违法失信行为信息记录”中的禁止参加政府采购活动期间。（以资格审查人员于投标（响应）截止时间当天在“信用中国”网站（www.creditchina.gov.cn）及中国政府采购网（http://www.ccgp.gov.cn/）查询结果为准，如相关失信记录已失效，供应商需提供相关证明资料）。(2)单位负责人为同一人或者存在直接控股、 管理关系的不同供应商，不得同时参加本采购项目（或采购包） 投标（响应）。 为本项目提供整体设计、 规范编制或者项目管理、 监理、 检测等服务的供应商， 不得再参与本项目投标（响应）。 投标（报价） 函相关承诺要求内容。三、获取招标文件时间： 2022年10月28日 至 2022年11月04日 ，每天上午 00:00:00 至 12:00:00 ，下午 12:00:00 至 23:59:59 （北京时间,法定节假日除外）地点：广东省政府采购网https://gdgpo.czt.gd.gov.cn/方式：在线获取售价： 免费获取四、提交投标文件截止时间、开标时间和地点2022年11月22日 09时30分00秒 （北京时间）递交文件地点：广东政府采购智慧云平台系统线上提交开标地点：广东政府采购智慧云平台系统远程开标五、公告期限自本公告发布之日起5个工作日。六、其他补充事宜1.本项目采用电子系统进行招投标，请在投标前详细阅读供应商操作手册，手册获取网址：https://gdgpo.czt.gd.gov.cn/help/transaction/download.html。投标供应商在使用过程中遇到涉及系统使用的问题，可通过020-88696588 进行咨询或通过广东政府采购智慧云平台运维服务说明中提供的其他服务方式获取帮助。2.供应商参加本项目投标，需要提前办理CA和电子签章，办理方式和注意事项详见供应商操作手册与CA办理指南，指南获取地址：https://gdgpo.czt.gd.gov.cn/help/problem/。3.如需缴纳保证金，供应商可通过"广东政府采购智慧云平台金融服务中心"(http://gdgpo.czt.gd.gov.cn/zcdservice/zcd/guangdong/)，申请办理投标（响应）担保函、保险（保证）保函。本项目支持电子保函，可通过登录项目采购电子交易系统跳转至电子保函系统进行在线办理。电子保函办理办法详见供应商操作手册。七、对本次招标提出询问，请按以下方式联系。1.采购人信息名 称：广东医科大学地 址：广东省湛江市霞山区文明东路1号联系方式：0759-23887332.采购代理机构信息名 称：广东省电信规划设计院有限公司地 址：0759-3386658联系方式：0759-33866583.项目联系方式项目联系人：吴娟、李静电 话：0759-3386658广东省电信规划设计院有限公司2022年10月28日

日前，布鲁克宣布收购Inscopix公司。Inscopix公司是神经科学的先驱，也是用于自由移动动物大脑成像的小型化显微镜（称为迷你显微镜）的市场领导者。自2011年成立以来，Inscopix公司的旗舰小型显微镜系统已被安装在全球600多家研究机构和生物制药公司，使基础神经科学研究取得突破，并促进了对神经系统疾病机制的理解。此次收购增强了布鲁克公司作为活体脑功能成像技术领导者的强大声誉，在细胞水平上使用Ultima多光子显微镜，在生物体水平上使用临床前MRI系统。

项目编号：TC229D00Q项目名称：锁相红外热成像系统和多功能X射线光电子能谱仪采购预算金额：505.0000000 万元（人民币）最高限价（如有）：505.0000000 万元（人民币）采购需求：分包号采购内容数量最高限价（万元）投标保证金（万元）中标人数量采购标的对应的中小企业划分标准所属行业一锁相红外热成像系统1套140.0021名工业二X射线光电子能谱仪1套365.0071名备注：1.本次采购可以采购进口产品，进口产品价格为最终交货价。2.各投标人均可就上述两个分包分别进行投标，同一投标人可中两个分包。3.以上招标内容的具体技术需求，见第二篇相关内容。合同履行期限：各分包中标人在合同签订之日起6个月内交货并完成安装调试，同时向采购人提供设备供货清单，由采购人确认。本项目( 不接受 )联合体投标。

脑功能成像探索生命领域的奥秘 联合研究合作方美国耶鲁大学医学院Joy Hirsch教授 我想通过fNIRS这一新技术对人与人的互动进行成像，以了解我们的脑如何适应实际生活和社会活动。比如，使用fNIRS，研究人与人之间的目光接触在交流中起到什么样的作用。我们与岛津制作所具有共同的价值观，希望能够作为伙伴长期一起合作。我不打算满足现状，岛津也是如此。正因为如此，我们才是伙伴。 在不断发展的脑科学研究中，可实现脑功能可视化的功能性近红外脑成像技术（fNIRS:functional Near-Infrared Spectroscopy），作为一种在日常环境中测量大脑活动的新方法而受到关注。 功能性近红外脑成像技术能够在安全、自然的状态下进行检测，对动静的限制较少，已被广泛应用于康复研究、药物开发、医学研究、精神和神经科学等研究领域。 功能性近红外光脑成像系统LABNIRS fNIRS的检测原理 脑内产生神经活动，周边区域的血红蛋白量即发生局部变化。fNIRS能够通过照射高生物透射性的近红外光，来检测吸收波长不同的含氧血红蛋白(Oxy-Hb)和脱氧血红蛋白（Deoxy-Hb），实时动画显示由脑活动引起的相对变化。 根据每个通道的时间序列数据的二维成像，安静时（左）与手指轻触时（右）的比较（Oxy-Hb） 功能性近红外光脑成像(fNIRS)的方案伦敦大学学院(UCL)的认知神经科学研究所，使用fNIRS，检测在莎士比亚剧中演员的脑活动模型。它用于研究人类社会认知和自闭症患者之间的社会交往差异。详情请扫描下方二维访问： PC端网址：https://www.shimadzu.com/about/momentum/feature/vol10.html 参考文献: Noah, J. A., Zhang, X., Dravida, S., Ono, Y., Naples, J. A., McPartland, J. C., & Hirsch, J. (2020). Real-time eye-to-eye contact is associated with cross-brain neural coupling in angular gyrus. Frontiers in Human Neuroscience 14(19), 1-10. doi: 10.3389/fnhum.2020.00019 Zhang, X., Noah, J. A., Dravida, S., & Hirsch, J. (2020). Optimization of wavelet coherence analysis as a measure of neural synchrony during hyperscanning using functional near-infrared spectroscopy.　Neurophotonics, In Press.

一、项目基本情况项目编号：OITC-G220290079项目名称：广东粤港澳大湾区国家纳米科技创新研究院多功能显微成像分析系统采购项目采购方式：竞争性磋商预算金额：159.0000000 万元（人民币）采购需求：包号货物名称数量简要技术要求是否允许采购进口产品采购预算 （人民币）1多功能显微成像分析系统1套详见技术参数是159万元包号货物名称数量简要技术要求是否允许采购进口产品采购预算（人民币）多功能显微成像分析系统1套详见技术参数159万元合同履行期限：合同签订后的四个月内交付到指定地点本项目( 不接受 )联合体投标。

近日，致真精密仪器的多功能磁光克尔显微成像系统入选了工业和信息化部装备工业一司的智能检测装备创新产品目录（第一批）。此活动是由智能检测装备产业发展联盟为贯彻落实《智能检测装备产业发展行动计划（2023-2025年）》，加快形成新质生产力，根据《关于征集智能检测装备创新产品的函》（工通装函〔2023〕538号）并受工业和信息化部装备工业一司委托，组织专家对征集产品进行遴选评选而来。经第三方机构遴选后，将建立智能检测装备创新产品项目库，为后续分类施策提供依据。成熟产品将优先推荐纳入到首台（套）保险补偿和市场推广。荣誉的取得是对致真精密仪器长期技术积累和持续创新精神的肯定，意味着公司产品“具有明确应用场景，可满足国家战略需求或具有广阔市场前景，技术水平处于国内领先或国际先进水平”。[1]智能检测装备是智能制造的核心装备，是制造业创新转型升级的关键环节。国务院在2024年两会结束后发布《推动大规模设备更新和消费品以旧换新行动方案》，围绕推进新型工业化，特别强调重点行业设备更新改造。致真精密仪器一直以来致力于实现高端科技仪器和集成电路测试设备的自主可控和国产替代，积极响应政策号召。本次活动入选的多功能磁光克尔显微成像系统，可对磁性材料和自旋电子器件进行高分辨磁畴成像，分辨率可达220纳米，能够清晰观察硅钢材料、永磁材料、纳米磁性薄膜、自旋电子器件中的磁畴变化，研究斯格明子磁泡、磁性材料缺陷等微观结构。为适应前沿科学研究和产品研发的多场景测试需求，配置高度智能化的控制系统和多功能磁场探针台，将光学成像、多维磁场、电学输运表征、微波测试、变温模块集成于一体，一键操作便能实现磁场、电流、自旋轨道矩、自旋转移矩等各种激励条件下的磁动力学过程观察。可在二次谐波、ST-FMR测量的同时，同步观察磁性变化；微秒级快速反应磁场，能够进行高精度磁畴速度测量和DMI测量。磁光克尔显微镜让磁学测试“眼见为实”！[1]《关于征集智能检测装备创新产品的函》（工通装函〔2023〕538号）创新产品征集要求（二）。

WITec 专业研发制造高分辨率、高灵敏度的共聚焦、快速拉曼成像显微系统。WITec 模块化的产品设计，可实现与 AFM、SEM、SNOM、SHG、超低温强磁场等多场技术联用，实现对同一样品进行光学分析、化学组分分析及2D/3D 结构表征，不仅能按需满足您当前的科研需求，还可以扩展功能助您应对未来挑战。1alpha300 系列 拉曼成像显微镜alpha300 系列：拉曼成像( alpha300 R )、原子力( AFM )、扫描近场光学显微镜( SNOM )及其联用系列高共聚焦、高分辨率、高灵敏度拉曼显微系统，以其优异前沿的成像技术倍受认可。灵活的模块化设计，还可以结合更多成像技术，为您定制个性化解决方案，实现原位化学组分分析和纳米级别表面形貌分析等科学研究。alpha300 SHG 将偏振谐波显微成像结合非线性光学效应与偏振共聚焦显微系统，已经广泛应用于科研领域。基于模块化的产品设计，不仅可以实现常规偏振 SHG / THG 测量及成像分析，还可以拓展为低温与磁场等极端条件下的非线性分析，实现传统及新型二位铁电材料与器件的精细分析表征。实验室排布2alpha300 apyron - 全自动拉曼成像显微镜alpha300 apyron 采用高精度自动化硬件控制和预设置光路模块，将易用性和高性能结合起来，扁平化实验工作流程，适用于：兼具不同操作水平和多功能需求的实验室要求高重复性试验场景、注重时效性的工业实验室有高级成像需求的拉曼新手寻求更高性能标准的资深拉曼光谱学家需远程操作的研究人员，如密闭环境操作3alpha300 Ri - 倒置拉曼成像显微镜alpha300 Ri 采用倒置光路对样品从下到上进行化学表征，既保留了 alpha300 系列共焦拉曼成像显微镜的功能，又引入全新的倒置光路设计，便于观察研究水溶液和大尺寸样品。 其独特的几何学设计，尤其适用于生命科学、生物医学和地质领域的研究。4alpha300 Semiconductor Editionalpha300 Semiconductor Edition 半导体定制版是一款专门为半导体材料行业研发的高端共聚焦拉曼显微镜。它能帮助研发人员加速对半导体晶圆和器件的晶体质量、应力与掺杂以及失效分析的表征工作。该款拉曼显微镜搭载大尺寸扫描台，可满足12英寸(30厘米)晶圆的大面积拉曼图像，配备主动隔振台和自动聚焦模块，保证其在测量期间可以对不同形貌样品进行大面积扫描或长时间采集。整套系统全部自动化，可远程控制，以保障工业标准流程测量。关键特性：高性能共聚焦拉曼显微镜，同时兼具快速、高灵敏度和高分辨率高端波长优化光谱仪 ，高信号灵敏度和光谱分辨率大面积扫描 (300 x 350 mm) ，适用于大尺寸晶圆检测大面积测量时实时追踪聚焦 (TrueSurface)主动隔振高度自动化远程控制和可重复性工作流程高级数据处理与分析软件5RISE - Raman - SEM 联用显微镜RISE 显微镜将拉曼成像与扫描电子显微镜功能集成到一台设备，可以进行超微结构表面特性与分子化合物信息关联分析。RISE 显微镜的应用领域可涵盖：材料科学纳米技术高分子地质科学生命科学制药产业6cryoRaman - 超低温强磁场拉曼显微镜cryoRaman 将极限空间分辨率的拉曼成像带到超低温-强磁场研究领域，强势助力低温磁场下材料新物理特性的研究，可轻松进行低至 1.8K 的强磁场实验。多功能关联成像测量：拉曼光谱及成像，荧光及其寿命及成像，二次谐波成像、微区光电流等。多领域应用：量子光学材料的磁光效应拉曼效应磁光材料结构相变、磁相变和磁振子激发研究低温磁场下材料相变的光谱特性磁场对光电材料的能带及载流子漂移影响半导体量子点发光的多体问题7alphaCART: 移动式光纤耦合共聚焦拉曼系统alphaCART 是一款移动式共聚焦拉曼系统，该系统可实现将“实验室”搬到检测现场，为您拓展特殊样品环境下的更多科研应用。alphaCART系统延续了alpha300系列拉曼显微镜的先进光学和模块化设计，并同样受益于WITec在光纤耦合技术方面的长期专业积累。通过光纤将激光器、探头和光谱仪连接，确保系统的高光通量和最佳的光束形状。因此，alphaCART 能提供与 WITec alpha300系列系统相媲美的衍射极限空间分辨率、高共聚焦性和优越的信号灵敏度。alphaCART 可搭载不同配置，以满足您对激发波长和光谱仪设置的特定要求。系统配备白光照明和彩色摄像机，以实现样品观察与定位，通过最新的 WITec Suite 软件 采集数据并完成数据后处理。alphaCART 系统还可以完整装入定制的可移动外箱（可选配）中，方便且安全地带到测试现场。此外，也可将系统的拉曼探头连接到实验室的标准 alpha300显微系统上，以拓展更多应用。

一、项目基本情况项目编号：OITC-G230320050项目名称：中国科学技术大学高分辨多功能化学成像系统-飞行时间二次离子质谱仪采购项目预算金额：820.000000 万元（人民币）最高限价（如有）：820.000000 万元（人民币）采购需求：1、采购项目的名称、数量：包号货物名称数量（台/套）是否允许采购进口产品1高分辨多功能化学成像系统-飞行时间二次离子质谱仪1是 投标人须以包为单位对包中全部内容进行投标，不得拆分，评标、授标以包为单位。2、技术要求详见公告附件。合同履行期限：详见采购需求本项目( 不接受 )联合体投标。二、获取招标文件时间：2023年09月28日 至 2023年10月11日，每天上午9:00至11:00，下午13:00至17:00。（北京时间，法定节假日除外）地点：www.oitccas.com方式：登录东方招标平台www.oitccas.com注册并购买。售价：￥600.0 元，本公告包含的招标文件售价总和三、对本次招标提出询问，请按以下方式联系。1.采购人信息名 称：中国科学技术大学　　　　　地址：安徽省合肥市金寨路96号 　　　　　　　　联系方式：0551-63602706 　　　　　　2.采购代理机构信息名 称：东方国际招标有限责任公司　　　　　　　　　　　　地　址：（北京）：北京市海淀区丹棱街1号互联网金融中心20层、（合肥）：合肥市高新区创新大道2809号置地创新中心28层2815室　　　　　　　　　　　　联系方式：（北京）窦志超、曹山、王琪 010-68290502、（合肥）：郑文彬、李文海0551-66030322　　　　　　　　　　　　3.项目联系方式项目联系人：窦志超、曹山、王琪、郑文彬、李文海电　话：　　010-68290502/0551-66030322

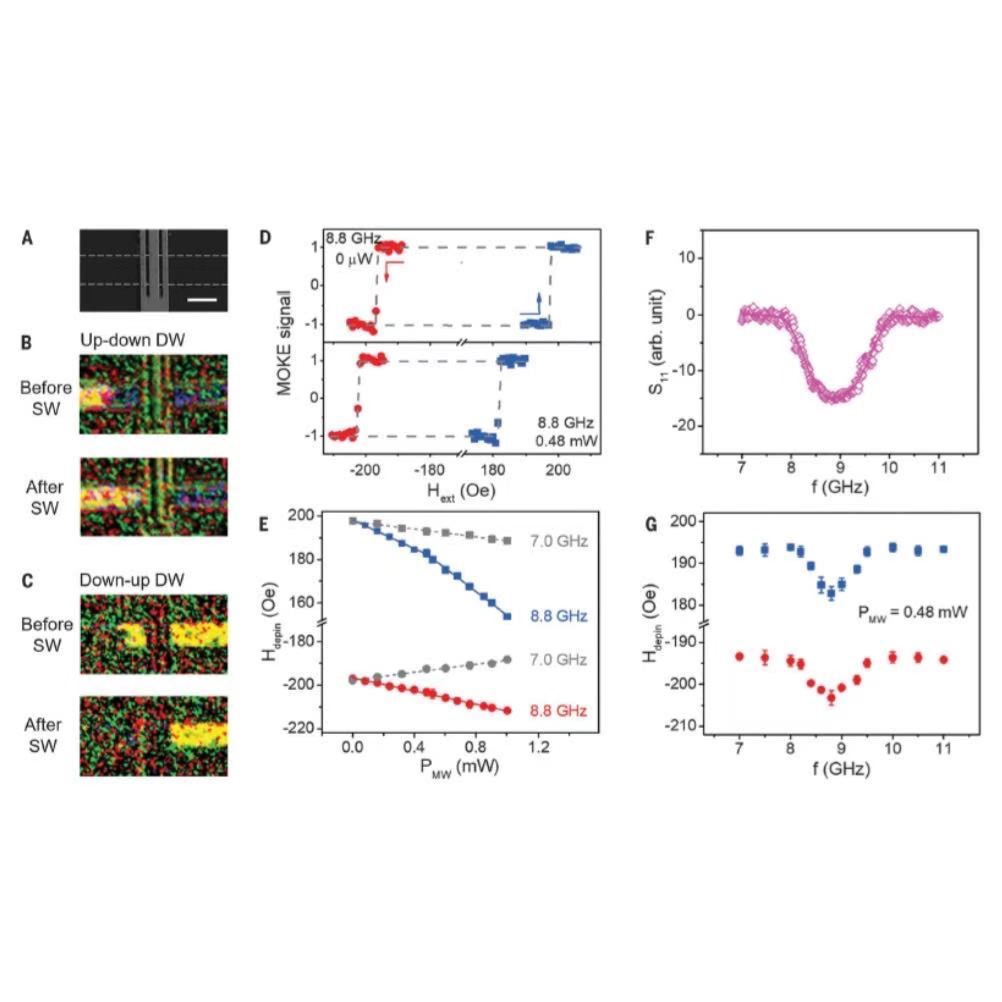
忆阻器是一类表示磁通与电荷关系的基础电路元件，也是构建人工神经网络的理想元件。传统忆阻器多数是基于材料内部的离子迁移和价带变化实现的，存在工作寿命短和反应速度慢等缺陷，无法支撑持续训练学习的神经网络的长时间工作[2]。与之相反，自旋电子器件基于材料内部的磁性变化工作，具有工作寿命长、反应速度快等优势[3-7]。长期以来，科学和产业界在不断地探索如何将磁隧道结等自旋器件应用于神经网络计算[8]。然而，经典的磁隧道结仅具有高、低二值阻态，无法在神经网络计算方面发挥优势。 2021年3月7日，北京航空航天大学集成电路科学与工程学院赵巍胜教授团队教师张学莹、博士生蔡文龙、教师王梦醒及潘彪以共同位作者，赵巍胜教授为通讯作者在Advanced Science期刊在线发表了题为“Spin‐Torque Memristors Based on Perpendicular Magnetic Tunnel Junctions for Neuromorphic Computing” 的学术论文[1]。赵巍胜教授团队设计了一种带有特自由层结构的磁隧道结，即在自由层中插入了单原子层的W，然后利用退火技术，让W形成聚簇效应，实现了一种基于垂直各向异性磁隧道结的自旋忆阻器，并在百纳米的器件中实现了稳定的近乎连续的多态，也是国际上次实现百纳米尺寸的可全电学操控的自旋忆阻器（如图1所示），有望为自旋电子器件在人工智能领域的应用打开道路。图 1 （a，b）该工作实现的自旋忆阻器件通过电压脉冲序列激励诱导的阻态变化；（c-e）器件的脉冲时序依赖可塑性验证。 该研究对这种新型器件的性质进行了全面的实验表征，验证了这种器件阻态的脉冲时序依赖可塑性（简称STDP，是脉冲神经网络的基础），证明了其构成的系统能够高效率、低功耗地实现手写数字识别等功能。 此外，该研究次发现了一种立体的手性涡旋结构（图2d）：在CoFeB/W/CoFeB构成的自由层中，CoFeB/W界面和W/CoFeB界面产生的Dzyaloshinskii-Moriya作用（DMI）相反，同时，两层CoFeB之间的耦合作用则随着W的厚度变化出现强度涨落或铁磁/反铁磁耦合交替。在局部区域W出现聚簇效应，反铁磁耦合与反向DMI联合作用，促使磁畴壁演变成手性涡旋结构，形成能量势阱。在磁隧道结自由层翻转过程中，这种涡旋结构会将运动的畴壁牢牢地钉扎住，从而形成了稳定的多阻态。图 2 (a)论文所用MTJ膜层中W原子的分布；（b）在反向DMI和不同RKKY耦合强度下CoFeB/W/CoFeB双磁层中可能存在的磁畴壁形态；（c）不同磁畴壁形态对应的能量；（d）在W原子聚簇区域由反向DMI和RKKY反铁磁耦合共同促进形成的立体涡旋结构示意图。 值得一提的是，Quantum Design中国与致真精密仪器（青岛）有限公司合作推出的多功能高分辨率磁光克尔显微成像系统对解析自旋忆阻器的工作原理分析和多态来源方面发挥了重要作用。 先，作者通过高分辨率磁光克尔显微镜观察了MTJ膜层自由层的磁性翻转过程，与磁滞回线测量结果进行了对照，发现文章所用膜层存在较强的磁畴钉扎作用（如图3）。同时，作者测量了该材料自由层中磁畴壁移动速度，通过蠕行公式（creep mode motion）拟合，提取了一个重要的参数：本征磁畴壁钉扎磁场Bdep，如图4a所示。这个磁场是表征磁性薄膜磁畴壁钉扎强度的标志性参数，低于该临界磁场，不考虑热扰动的情况下，磁畴壁无法运动。经对比发现，薄膜中提取的该磁场与忆阻器件中多态在低温下的临界稳定磁场几乎相等，由此确定了自旋忆阻器件的多态来源于磁畴钉扎（图4b）。以磁光克尔显微镜为工具，通过磁畴壁速度测量提取磁畴壁本征钉扎磁场强度，是少有的能够定量评估磁性薄膜质量和畴壁钉扎强度的方法，在开发新材料，优化自旋电子器件性能方面得到广泛应用[7][9]。 图 3 利用高倍磁光克尔显微镜观察到的该自旋忆阻器自由层中磁畴扩张状态与磁滞回线的对应关系。图 4 （a） 磁光克尔显微镜测量的CoFeB/W/CoFeB磁性薄膜（蓝）与普通CoFeB薄膜（红）中磁畴中磁畴壁运动速度的比较；以及CoFeB/W/CoFeB中内禀钉扎磁场（16.3 mT）与（b）器件在低温下的多态稳定磁场（去除偏置后为15.5 mT）的比较。 在CoFeB/W/CoFeB自由层薄膜中，为什么会有如此强的磁畴壁钉扎作用呢？作者利用磁光克尔显微镜，从DMI、海森堡交换作用强度等多个角度进行了细致表征。先，分别定量测量了sub/MgO/CoFeB/W薄膜、sub/W/CoFeB/MgO两种镜面对称薄膜结构的DMI，发现两种膜层的DMI手性相反且强度相当（图5）。随后，测量了多态器件所用的自由层薄膜CoFeB/W/CoFeB的DMI，强度几乎为零。由此推测，CoFeB/W界面和W/CoFeB的DMI被中和。另一方面，通过透射电镜，作者观察到了CoFeB/W/CoFeB中W原子的分布并不均匀，局部出现了聚簇，W原子垒叠成2层甚至3层，而多数区域W原子则为单层甚至出现断裂。依据S. Parkin测量结果[10]，双原子层的W能够使上下两层铁磁材料发生RKKY反铁磁耦合。进一步，作者通过微磁仿真，结合磁光克尔成像获得了关于DMI，海森堡交换作用（测量方法见该文章附加材料[1]）等参数，证明在具有W聚簇的区域，能够形成上下层手性相反的的垂直涡旋结构。而且，这种涡旋结构具有较低能量，在磁畴壁经过之时，能够形成强烈的钉扎作用。图 5 利用磁光克尔显微镜测量不同薄膜结构中磁畴壁运动的速度以及DMI的提取。 磁光克尔显微镜除了能够获得高分辨率的动态磁畴观测外，在磁性薄膜材料和自旋电子器件动力学分析领域也有着突出的优势，它能够直观、高效、无损地测量多种参数，包括饱和磁化强度、各向异性强度、海森堡交换作用强度和DMI强度等。通用型的磁光克尔显微镜很难对这些磁学参数进行直接的测量，为了降低使用门槛，使磁光克尔成像和磁畴动力学分析技术在磁学和自旋电子学中发挥更大作用，张学莹老师在多年积累的测试经验和仪器配置方案基础上，开发出了一款多功能、智能化的多场高分辨率磁光克尔成像系统。该系统能够让用户利用软件定义电、磁等多种想要的波形，一键触发后，在样品上同步施加垂直/面内磁场、电流脉冲、微波信号，可同时进行磁光克尔成像和电阻等参数的测量。这种多功能的设备将电输运测试和磁光克尔成像结合，预期将在自旋轨道矩、斯格明子磁泡动力学等方面发挥更大作用。 目前，这款多场高分辨率磁光克尔成像系统已经获得了清华大学、中国科学院物理研究所、北京工业大学、上海科技大学等客户多套订单。 图6多功能高分辨率磁光克尔显微成像系统 产品基本参数：向和纵向克尔成像分辨率可达300 nm；配置二维磁场探针台，面内磁场高达1 T，垂直磁场高达0.3 T（配置磁场增强模块后可达1.5 T）；快速磁场选件磁场反应速度可达1 μs；可根据需要选配直流/ 高频探针座及探针；可选配二次谐波、铁磁共振等输运测试；配置智能控制和图像处理系统，可同时施加面内磁场、垂直磁场和电学信号同步观测磁畴翻转；4K~800K，80K~500K 变温选件可选。 参考文献 [1] X. Zhang#, W. Cai#, M. Wang#, B. Pan#, K. Cao, M. Guo, T. Zhang, H. Cheng, S. Li, D. Zhu, L. Wang, F. Shi, J. Du, and W. Zhao*, Adv. Sci. 2004645, 2004645 (2021).[2] M. A. Zidan, J. P. Strachan, and W. D. Lu, Nat. Electron. 1, 22 (2018).[3] X. Lin, W. Yang, K. L. Wang, and W. Zhao*, Nat. Electron. 2, 274 (2019).[4] M. Wang, W. Cai, K. Cao, J. Zhou, J. Wrona, S. Peng, H. Yang, J. Wei, W. Kang, Y. Zhang, J. Langer, B. Ocker, A. Fert, and W. Zhao*, Nat. Commun. 9, 671 (2018).[5] M. Wang#, W. Cai#, D. Zhu#, Z. Wang#, J. Kan, Z. Zhao*, K. Cao, Z. Wang, Y. Zhang, T. Zhang, C. Park, J. P. Wang, A. Fert, and W. Zhao*, Nat. Electron. 1, 582 (2018).[6] S. Peng#, D. Zhu#, W. Li, H. Wu, A. J. Grutter, D. A. Gilbert, J. Lu, D. Xiong, W. Cai, P. Shafer, K. L. Wang, and W. Zhao*, Nat. Electron. 3, 757 (2020).[7] X. Zhao#, X. Zhang#, H. Yang#, W. Cai, Y. Zhao, Z. Wang, and W. Zhao*, Nanotechnology 30, 335707 (2019).[8] X. Zhang, W. Cai, X. Zhang, Z. Wang, Z. Li, Y. Zhang, K. Cao, N. Lei, W. Kang, Y. Zhang, H. Yu, Y. Zhou, and W. Zhao*, ACS Appl. Mater. Interfaces 10, 16887 (2018).[9] X. Zhao et al., Appl. Phys. Lett. 115, (2019).[10] S. S. P. Parkin, Phys.Rev.Lett. 67, 3598(1991)

项目编号：JXBJ22121372301项目名称：南昌大学第一附属医院科研仪器设备采购项目采购方式：公开招标预算金额：2390000.00 元最高限价：2390000.00采购需求：采购条目编号采购条目名称数量单位采购预算（人民币）技术需求或服务要求赣购2023F000827953二氧化碳培养箱2台90000.00元详见公告附件赣购2023F000827955超灵敏多功能成像仪2台590000.00元详见公告附件赣购2023F000827952快速湿转仪1台50000.00元详见公告附件赣购2023F000827950多功能酶标仪1套600000.00元详见公告附件赣购2023F000827951无创脉搏血氧仪1套220000.00元详见公告附件赣购2023F000827954活细胞荧光显微成像系统1台380000.00元详见公告附件赣购2023F000827956生物反应器1台460000.00元详见公告附件合同履行期限：合同签订生效后120个日历日内完成安装调试并交付使用。本项目不接受联合体投标。

项目编号：TC229D00Q项目名称：锁相红外热成像系统和多功能X射线光电子能谱仪采购预算金额：505.0000000 万元（人民币）最高限价（如有）：505.0000000 万元（人民币）采购需求：分包号采购内容数量最高限价（万元）投标保证金（万元）中标人数量采购标的对应的中小企业划分标准所属行业一锁相红外热成像系统1套140.0021名工业二X射线光电子能谱仪1套365.0071名备注：1.本次采购可以采购进口产品，进口产品价格为最终交货价。2.各投标人均可就上述两个分包分别进行投标，同一投标人可中两个分包。3.以上招标内容的具体技术需求，见第二篇相关内容。合同履行期限：各分包中标人在合同签订之日起6个月内交货并完成安装调试，同时向采购人提供设备供货清单，由采购人确认。本项目( 不接受 )联合体投标。

赵工李工，最近看你的工作效率很高呀，是有什么秘诀吗？求分享呀~秘诀谈不上，就是最近新添置了一个称手的工具——FLIR CM275，它既可以查明电气故障根源，还可以协助我做出正确的诊断，大大缩短了我的工作时间。李工FLIR CM275数字钳形表将红外成像与电气测量功能相结合，是强大的检测、故障排除和诊断工具。它到底是如何替李工提高工作效率？今天，小菲就来给大家揭开这个谜题！FLIR CM275视频详细解析01快速发现，安全定位FLIR CM275采用IGM红外成像引导测量技术，提供一种在安全距离内识别热点和过载电路的可靠方式，让您能够快速识别问题，无需直接接触可能存在安全隐患的配电柜和电气柜或凌乱不堪的电线和电缆。★ 借助高达160×120像素的热分辨率，快速扫描整个目标存在的电气问题；★ 借助激光指示器和十字准线确定热点的准确位置；★ 得益于细长夹钳与内置照明灯，可轻松检测难于接触、光线昏暗的位置；★ 符合CAT?IV-600V、CAT?III-?1000V安全等级要求，为您提供可靠防护。02确认问题，验证热点FLIR CM275借助数字钳形表的丰富功能获取精确的电流和电压读数以及中心点读数，采用2.4英寸TFT屏，便于查看数据和图像。★ 借助高压和低压测量功能，诊断错综复杂的系统；★ 使用高级电气测量功能，包括VFD模式、真有效值、LoZ(低阻抗输入)；★ 通过使用FLIR柔性电流钳可将交流、电流测量范围扩展至3000安培。03及时记录，方便分享FLIR CM275还具有无线连接功能，可直接连接至FLIR Tools™ 或FLIR InSite™ 专业工作流管理应用程序，让工作更加轻松。借助该应用程序，您可以上传与整理电气测量值和热图像，与您的团队分享信息，以及在现场提交即时报告。带数据记录功能的FLIR CM275 IGM™ 钳形表，是面向电气、机械和电子系统的理想多功能故障排除工具.

2023年7月8日，在江苏省研究型医院学会器官芯片分会成立大会召开期间，艾玮得生物于大会现场正式发布了AvatarInsight高内涵智能成像分析仪。AvatarInsight高内涵智能成像分析仪亮点一. 高速自动定位对焦■高精度识别待检测样本孔位及自动对焦，快速找到理想的成像焦面。■96孔整板精细对焦拍照可在5分钟内实现。亮点二. 孔板滴定导航与多通道采集孔板滴定导航■记录孔板孔位位置，实时/定时拍照。■使用每个孔多个观察点位的自定义采集模式。多通道采集可同时观察多色样品，结合相衬等其他成像模式，通过自动曝光和每个通道的Z偏移，在最佳条件下快速采集图像。亮点三. 丰富的拍摄模式延时/周期拍摄■持续记录活细胞或整个培养物随时间的变化。■与给药装置结合使用，实时观察给药细胞的即时反应。视频拍摄记录孔板孔位位置，实时/定时拍照。在样本观察过程中可选择视频拍摄，拍摄持续时长可达24H，更加有利于实验样本变化的动态记录。小鼠肠道类器官培养周期拍摄肝癌类器官培养周期拍摄亮点四. 超高清的成像高精画质自动切换Koehler照明不同模式，生成对应光学图像，可同时进行明场、相差、荧光高分辨率观察，并始终保持成像画质的高精确度。荧光成像原片(左) 白平衡(中) 相差(右)全景拼接以高分辨率快速采集组织样品或评估大面积细胞培养瓶的状况，清晰呈现全景图像；实现图像的高精度拼接、无拼接缝隙。Z-stack沿Z方向采集多个图像以适应厚样品；轻松点击即可创建全景在焦清晰图像。亮点五. AI智能算法与数据管理兼容丰富多样的样本来源，包括肝脏、胰腺、结肠、肺、心肌细胞、毛细血管等等组织器官的智能识别与分析。AI识别算法强大的智能训练单元能够即时、快速地完成特征提取，智能匹配类似特征样本，进而完成样本AI识别。AI分析算法可针对类器官、肿瘤球等实验项目进行AI分析。其中，智能识别类器官3D形态并进行涂色后，可完成类器官数量、大小和形态等各项指标的AI分析；AI描绘肿瘤球边际，并根据描边各项数据智能分析肿瘤球的入侵程度。快速、高效的数据管理功能具有快速、高效的数据管理功能，确保数据组织有序，可供反复调用，并有效避免混淆。亮点六. 便捷与友好的产品设计精密的光学技术■5孔位物镜转盘让您快速便捷地使用多种倍率观察样品。■实时呈现多荧光波段，丰富实验染料选择，为观测样本提供便捷性。倍镜依次：2X、4X、10X、20X、40X荧光：BP330-385 BP450-490 BP530-560BP545-580防污装置，可有效保护光学附件高内涵观测口设置的防污装置，可提供光学附件的保护，有效提升设备使用寿命。可拓展性高艾玮得生物科技全流程追溯与分析软件系统高内涵图片实时对接实验步骤和实验内容；实时记录和追溯样本和实验信息，包括实验步骤管理、试剂耗材管理等；可支持客户端安装、远程云端网页和微信小程序使用。细胞成像环境控制系统AvatarInsight高内涵智能成像分析仪可搭载细胞成像环境控制系统，用于活细胞在线研究，满足荧光、共聚焦等观察需求，可在显微镜载物台上为活细胞提供适宜的温度、湿度、二氧化碳、氧气环境，是活细胞观察系统必不可少的设备之一。

近日，国家级创新平台——公路养护技术国家工程研究中心自主研发的多功能路况快速检测系统(CiCS)获得英国SCANNER认证。迄今为止，除我国之外，只有英国、加拿大、瑞典三个发达国家的同类技术获得了SCANNER认证。 　　英国是世界上公路养护管理技术最为发达的国家之一，也是自动化检测技术研发与应用最早的国家。英国的SCANNER认证是检验设备性能、获得国际认可的重要渠道，被认为是“世界上最严格的认证”。 　　CiCS成功通过英国SCANNER认证，标志着我国公路路况快速检测技术及高端装备工程化研发制造能力达到国际领先水平，改变了该领域长期被发达国家技术垄断的局面，为我国公路养护自主创新成果深度参与国际竞争奠定坚实基础。

凝胶成像系统一般由CCD（电荷耦合器件）相机、光源、暗室和分析软件等部分构成，是分子生物学和生物化学研究的必备工具，常用于对蛋白质、多肽以及核酸等生物分子作定性、定量分析。其中，CCD相机在凝胶和印迹成像系统中已有超过30年的应用历史。然而，近年来CMOS（互补金属氧化物半导体）传感器性能的大幅提升为科学成像应用领域提供了另一种可能。2024年5月，伯乐（Bio-Rad）正式推出了首款搭载冷CMOS传感器的ChemiDoc Go荧光及化学发光成像系统，具有更高的光电转化效率和更大的像素密度（超2000万像素），并采用全LED光源设计不仅提升了系统性能，并具有超长使用寿命。2024年9月13日，全球科学仪器新品发布会暨“突破创新”主题论坛在北科建怀柔国际创新中心成功举办。仪器信息网特别采访了伯乐生命医学产品（上海）有限公司应用技术专家王恒，围绕新品ChemiDoc Go成像系统创新亮点、CCD与CMOS技术差异、凝胶成像技术发展趋势及市场前景展开深入探讨。以下是视频采访详情：仪器信息网：贵司今天带来的ChemiDoc Go荧光及化学发光成像系统最大创新亮点是什么？王恒：ChemiDoc Go是伯乐在2024年推出的一款全新成像系统，使用了最新的超高像素CMOS传感器代替传统的CCD传感器，并在保持成像功能增多性能变强的同时，还进一步缩小了机身体积，是一款现代化的智能成像平台。仪器信息网：作为伯乐首款搭载CMOS传感器技术的凝胶成像系统，与传统CCD成像相比，有哪些技术优势？王恒：无论CCD还是CMOS都是采用感光元件作为影像捕获的基本手段，其感光元件的核心也都是光电二极管。唯一区别在于读出方式的不同，CCD传感器每个像素输出的是电荷量，属于模拟信号，需要额外的电压驱动电路和转换器；而CMOS传感器每个像素都集成了放大器与转换器，可以直接输出数字信号，因此，成像速度上会有明显的提升。另外，得益于集成电路的设计水平及生产工艺的提升，本次ChemiDoc Go搭载的CMOS传感器光电转化效率更高，对制冷温度的要求也没有以往CCD那么严格，成像效果更加清晰灵敏的同时也更加节能。仪器信息网：未来几年内，凝胶成像技术将如何发展？会有哪些新兴技术与凝胶成像系统相结合？王恒：我认为未来凝胶成像技术将会向高精度、自动化、多功能和智能化方向发展。相信随着伯乐首款采用冷CMOS成像系统的推出，未来将有更多品牌采用CMOS传感器替代传统CCD传感器。同时，伴随着芯片技术和材料科学的快速发展，成像系统的灵敏度将会越来越高。对于新兴技术而言，我认为大数据分析、AI模型可能会植入到凝胶成像系统内。现代实验室越来越追求高效、精准的工作流程，具备自动化曝光成像、智能图像识别与分析功能的凝胶成像系统将极大提升实验效率与数据质量。大数据AI模型能够自动识别样本类型、智能优化曝光条件，并通过算法辅助分析实验结果，减少人为误差，当出现不满意的拍照结果时甚至能够进行Troubleshooting，找到拍照结果不理想的原因以及改善建议，使科研人员能够专注于科学问题的探索而不是繁琐的实验操作流程。仪器信息网：您如何看待凝胶成像系统市场现状以及未来前景？王恒：随着生物医药行业的蓬勃发展，凝胶成像系统作为科研实验室的必备工具，其市场正处于一个上升阶段，孕育着诸多投资机遇。尤其在国内，随着经济增长和科研投入的持续增加，凝胶成像系统的市场潜力显得尤为巨大。与此同时，行业内竞争日益加剧，众多国产品牌纷纷进军凝胶成像领域，导致产品同质化问题愈加突出。可以预见，随着生物技术的进步和科研资金的持续注入，凝胶成像系统的市场需求将不断攀升，特别是对高端、多功能产品的需求将更加旺盛。品牌方则需通过技术创新、优化生产流程、完善售后服务等方式提高产品竞争力，满足多元化的用户需求。鉴于目前凝胶成像市场竞争已进入到白热化阶段，未来如果没有颠覆性的新技术出现，单一品类将很难获得成功，只有将品牌与技术的优势整合成系统性的完整实验解决方案，或者说是构建“品牌生态”，并不断创新，才能够真正的打动用户，占领市场。

一、项目基本情况1.项目编号：1499002023AGK007912.项目名称：分子医学中心多功能酶标仪等设备项目3.预算金额：人民币伍佰伍拾捌万伍仟元整（￥5585000.00） 最高限价：人民币伍佰伍拾捌万伍仟元整（￥5585000.00）4.采购需求：本项目不分包。采购明细见下表：序号品目名称采购数量预算金额（万元）最高限价（万元）简要技术需求备注1多功能酶标仪2套7070连续波长检测系统&高灵敏度滤光片&优化二向色镜光路设计；配三种检测模块：可见/紫外光吸收、荧光强度、化学发光检测模块进口2实时荧光定量PCR仪2套7070用于基因表达分析研究，目的基因的定量分析，进行SNP单核苷酸多态性和突变位点的分析检测进口核心产品3大容积冰箱1组（6台）22制冷方式：风冷；总容积：≥535L；能效等级：一级能效；控温方式：电脑控温4立式压力蒸汽灭菌器4台2828设计容积≥83L，有效容积≥75L；灭菌温度：115~135℃，最小分度值0.1℃，溶解温度：60~110℃，最小分度值0.1℃保温温度：45~60℃，最小分度值0.1℃。5全自动核酸提取仪1套4949适用样本：全血、血浆、血清、新鲜冰冻组织、培养细胞、尿液、拭子、痰液、脑脊液、粪便等进口6活体测试设备1台3232系统可以灵活调节光敏感度，可以应对不同体重的动物；系统通过内光源折射方法全自动识别和分类四只脚印，自动计算脚印和步态参数7光纤激光器(成套)3套16.516.5波长以及性能660nm+/-6nm2.0W，808nm+/-10nm5.0W；980nm+/-10nm8.0W；1064nm+/-2nm5.0W；功率稳定性 5%8样品干燥设备(成套)2套3636整套设备由：真空干燥箱*2、鼓风干燥箱*6、马弗炉*2、气氛微波管式炉*2、旋转蒸发仪*1、冻干机*3、低温冷却液循环泵*1、玻璃气流烘干器*5组成；9单道进口移液器(成套)50套5050量程范围：0.1-2.5ul；0.5-10ul：2-20ul：10-100ul；20-200ul；100-1000ul；1-10ml进口10合成反应设备(成套)2套5050整套设备由：实验室制冰机*2、混匀仪*4、循环水真空泵*2、非接触式全自动超声破碎仪*2、实验室半微量电子天平*5、超声波清洗机*3、电化学工作站*1,微波合成系统*1组成；11实验室系列离心机5套1010整套设备由：低速离心机*1、高速离心机*1，离心机配套转子和套筒3套以上组成；12合成搅拌设备(成套)2套3636整套设备由：磁力搅拌器*40、集热式搅拌器*60、六联电动搅拌器*10、高温磁力加热套*5组成13超微量紫外分光光度计1套2020波长范围：190－850nm连续波长全光谱分析；光程：内含0.03,0.05,0.1,0.2,1mm5个光程，根据样品浓度进行自动匹配最佳光程14微循环动态影像系统1套4040监控相机：成像区域大于18×12cm。测量技术：基于激光散斑对比成像技术，可对大面积组织进行非接触及实时的血流动态成像监测，可为待测组织（如血管、皮肤、口腔内皮等）提供实时动态监测曲线和血流视频记录。功能成像速率（血流图像）：1-20帧/秒可调15微流控设备1套4949设备组成：紫外光刻机*1,注射泵*1,制胶系统*1,光刻胶*4,等离子清洗机*1,细胞电阻仪*1合计558.5558.55.上述内容中未特别标注为“进口”字样的，均必须采购国产产品。本项目其他采购需求的具体内容，以招标文件中商务、技术和服务的相应规定为准。6.合同履行期限：具体详见技术需求书。品目1、品目2、品目5：合同签订后40日内交货；品目3、品目4、品目8、品目9、品目10、品目11、品目13：合同签订后30日内交货；品目6、品目7、品目12、品目14：合同签订后45日内交货；品目15：合同签订后30个工作日内交货；7.本项目不接受联合体投标。项目编号：1499002023ACS00809项目名称：山西医科大学第一医院分子医学中心倒置荧光显微镜等设备采购项目采购方式：竞争性磋商预算金额：328.0000000 万元（人民币）最高限价（如有）：328.0000000 万元（人民币）采购需求：本次磋商共二包，供应商可对其一包或多包进行响应，所投包内项目必须完全响应磋商文件所列示内容。（具体内容、配置、技术要求等详见磋商文件）包号序号产品名称数量要求简述最高投标限价总金额（万元）备注第一包1倒置荧光显微镜2台主机：超强合金材料；92进口2正置荧光显微镜2台用途：该仪器主要用于观察组织形态和荧光标记92进口第二包1超低温冰箱4台内部容积：不小于 549L，2 英寸冻存盒的存放数量：不少于 400 个26/2进口纯水超纯水一体机4台满足实验室用III级水及I级水纯水的应用要求。58进口3细胞间设备（CO2培养箱*4，超净工作台*4，高速冷冻离心机*2，自动细胞计数器*2，液氮罐*4，加热制冷型恒温金属浴*4，细胞摇床*4，真空吸液系统*4）1组CO2培养箱*41 HEPA过滤器和高温干热灭菌技术，减少污染。 60/ 注：（1）采购内容中未特别标注为“进口产品”字样的，均必须采购国产产品。所采购的货物、服务必须符合国家的强制性标准。（2）供应商的报价不得超过最高限价，否则视为响应无效。（3）第二包进口纯水超纯水一体机为核心产品，若出现相同品牌，按照第三部分评审标准和评审方法正文第四条处理。采购范围：包括货物的供应、运输、安装、调试、培训和售后服务等。具体报价范围、采购范围及所应达到的具体要求，以磋商文件中商务、技术和服务的相应规定为准。采购需求：详见磋商文件第四部分商务、技术要求。合同履行期限：详见磋商文件本项目( 不接受 )联合体投标。项目编号：项目名称：山西医科大学第一医院分子医学中心激光共聚焦显微镜项目采购方式：竞争性磋商预算金额：380.0000000 万元（人民币）最高限价（如有）：380.0000000 万元（人民币）采购需求：货物名称数量单位最高限价简要规格描述备注激光共聚焦显微镜1套380万元通过可见激光对线虫，活细胞、组织和切片进行连续扫描，获得精细的单个细胞或一群细胞的各个层面结构（包括染色体等）的三维图像。可利用荧光标记测定细胞内如钠、钙、镁等离子浓度的比率、动态变化及pH值的动态变化进口产品合同履行期限：合同签订后 40 天本项目( 不接受 )联合体投标。二、获取招标文件1.时间：2023年6月1日00时00分00秒至2023年6月8日00时00分00秒（北京时间）2.获取地点：山西政府采购平台-政采云平台(https：//login.sxzfcg.zcygov.cn/user-login/#/login)线上获取；3.获取方式：政采云平台线上获取。不接受现场报名。

项目编号：GZWH-2022-23111 项目名称：贵州医科大学多功能食品研发及卫生分析检测采购项目--食品功能成分功效作用挖掘科研仪器设备采购项目 项目序列号： P520000202200052X 预算金额（元）：5137200最高限价（元）：4851800采购需求：标项名称: 贵州医科大学多功能食品研发及卫生分析检测采购项目--食品功能成分功效作用挖掘科研仪器设备采购项目 数量: 1 预算金额（元）: 5137200 简要规格描述或项目基本概况介绍、用途：贵州医科大学多功能食品研发及卫生分析检测采购项目--食品功能成分功效作用挖掘科研仪器设备采购项目招标项目的潜在投标人应在贵州省公共资源交易中心网上获取（交易中心网址：http://ggzy.guizhou.gov.cn/） 获取招标文件 。贵州医科大学多功能食品研发及卫生分析检测采购项目--食品功能成分功效作用挖掘科研仪器设备采购项目于2023年1月3日 9时30分0秒（北京时间） 前递交投标文件。 备注：无合同履约期限：标项 1，详见招标文件本项目（否）接受联合体投标。 贵州医科大学多功能食品研发及卫生分析检测采购项目--食品功能成分功效作用挖掘科研仪器设备采购项目_采购文件.pdf

近日，北京易科泰生态技术有限责任公司《FluorTron® 多功能高光谱成像分析技术及其应用》一文被“科创中国”科研仪器案例库正式收录。该活动由中国科学技术协会主办，旨在鼓励实验技术人员围绕国产仪器开发、应用撰写案例，助推国产仪器示范推广。 文章基于易科泰生态技术公司自主研发的FluorTron® 多功能高光谱成像分析技术，通过三个典型应用案例，印证了该技术可以在成像和光谱水平上解码生物荧光现象，灵敏检测解析植物对光系统II电子传递链阻断剂DCMU的时空和光谱响应、活体（in vivo）成像分析银杏叶黄酮含量等，具备高通量、非损伤、可视化等优势，可应用于植物表型分析、黄酮及花青素等次级代谢产物成像分析等。 FluorTron 多功能高光谱成像技术——解码生物荧光1) 多激发光叶绿素荧光高光谱成像，叶绿素荧光成像分析与荧光光谱分析，全面解析植物（包括藻类）光合生理生化信息2) UV-MCF紫外光激发生物荧光高光谱成像分析，同步成像分析叶绿素荧光、蓝绿荧光空间异质性分布及生物荧光光谱特征。3) （反射光）高光谱成像分析4) 可选配GFP、荧光素酶等生物活体荧光成像，用于转基因标记等5) 可选配成像室温控系统及温控载物台6) FluorVision专业荧光成像分析软件7）可应用于：a) 植物表型成像分析，特别适合叶片、种苗、根系等表型成像分析b) 种质资源研究检测鉴定，包括种子活力、萌发检测、种子分捡模型构建、种质资源数字化等，可同时采集构建种子反射光光谱指纹和荧光光谱指纹c) 作物遗传育种，如作物胁迫检测与生理生态研究分析、抗性筛选、高光效优良品种筛选等d) 智慧农业、光生物学研究，采后生物学研究e) 食品、中药材品质检测鉴定，珍贵中药材光谱指纹（包括反射光光谱指纹和荧光光谱指纹），劣质或掺假检测等f) 环境科学研究，如污染生态学、环境毒理学研究检测分析等

瑞士Cytosurge AG公司的多功能单细胞显微操作系统FluidFM BOT，是将原子力系统、微流控系统、细胞培养系统合为一体的单细胞操作系统，采用不同孔径的微型纳米注射器，可实现单细胞注射（Injection）、活细胞内物质提取（Extraction）、单细胞分离（Isolation）、粘附力测定（Adhesion）、纳米打印(Nano-printing)等多种功能，全程机械臂操纵，将污染风险和人为误差降到低，提高工作效率与实验可重复性，具有高度自动化、操作速度快与操作度高等特点，能够在单细胞水平上为研究者提供大的便利，可应用于单细胞质谱、单细胞力谱、单细胞基因编辑、细胞系构建、药物研发、医疗等领域。北京大学生命科学学院公共仪器中心的多功能单细胞显微操作系统FluidFM BOT，是国内套多功能单细胞显微操作系统，于2020年9月顺利安装于金光楼126室并开始试运行，由公共仪器中心覃思颖老师负责接样测试与维护管理。目前本中心的FluidFM BOT系统已成功应用于单细胞注射与物质提取（小鼠体外培养原代海马神经元、昆虫叶蝉细胞、MDA-MB-231细胞等）、单细胞分离（植物细胞原生质体、U2OS细胞等）与粘附力测定（细菌侵染细胞时细菌的粘附力、血管内皮细胞对不同基底的粘附力等）等多方面科研需求。以下是多功能单细胞显微操作系统FluidFM BOT的多个功能应用与实例介绍。FluidFM BOT结合原子力系统、微流控系统于一体（https://doi.org/10.1021/nl901384x）FluidFM BOT功能应用单细胞注射实例FluidFM BOT可以将多种不同类型的可溶性物质注入细胞核或细胞质中，可量化注射体积（fL别），可实现批量注射（每小时注射超过100个细胞），尤其适用于使用传统方法难转染的细胞，且对细胞几乎没有损伤。CHO细胞的Lucifier Yellow染料注射C57小鼠体外培养原代海马神经元DIV7的Dextran染料注射（北大生科院数据）活细胞内物质提取实例FluidFM BOT系统的活细胞内物质提取功能十分温和，可直接用微型纳米注射器吸取活细胞的细胞质或细胞核中的物质，无需经过化学或生物学手段进行破膜处理，不会产生裂解的细胞碎片，不会对内部细胞器造成任何破坏，可用于电镜成像、酶活检测、核酸表达检测、代谢组学、基因测序等多方面研究。活细胞提取物可结合电镜观察、酶活测定、转录检测等分析手段（http://dx.doi.org/10.1016/j.cell.2016.06.025）HeLa细胞的细胞质物质提取单细胞分离实例FluidFM BOT可进行无损细胞分离，对于悬浮细胞，可将细胞吸取并转移释放即可。对于贴壁细胞，可在探针的样品池中加入消化液如胰酶，对指定位置的细胞进行消化，然后再进行吸取与转移释放。FluidFM BOT实现的单细胞分离存活率很高，结合单细胞注射可实现快速转染细胞并建立单克隆细胞群，对于工程细胞株的建立十分有效。植物原生质体的单细胞分离（北大生科院数据）贴壁细胞CHO的单细胞分离粘附力测定实例FluidFM BOT系统通过负压将细胞吸附在探针针孔处，对细胞的吸附力比蛋白结合更加牢固，能够直接将细胞从基底上分离。这种方法不需要激活细胞的任何信号通路，可以得到接近细胞原生的数据。不同的探针针孔直径（2、4、8um）可适用于不同大小的细胞粘附力测定，我们甚至可使用孔径为300nm的探针进行更小个体的吸附与粘附力测定，目前在本中心的FluidFM BOT系统已成功应用于金黄色葡萄球菌侵染大鼠肠上皮细胞时的细菌粘附力测定（nN别）。不同大小的单细胞粘附力测定（https://doi.org/10.1038/s41598-019-56898-7）纳米打印实例FluidFM BOT系统还是一台纳米打印设备，可以在实验器材上铺设特定的基底膜，如打印亲水或亲脂性物质，从而实现对细胞贴壁的操纵，构建不同的细胞模式，实现对细胞信号转导机制、肿瘤细胞群落迁徙、神经细胞树突或轴突形成的研究。CMD基底打印cRGDfK的细胞贴壁生长Pattern研究（DOI: 10.1021/acs.langmuir.8b03249）多功能单细胞显微操作系统在高性能单元的监控下，通过全自动的工作站实施操作，可确保实验的平稳、顺利的进行。探针有多种孔径规格可选，也可结合FIB技术进行探针定制，结合不同的探针可实现各式各样的应用，以上仅展现部分应用，更多的新功能有待各位老师与同学结合自己的课题需求进行探索与发掘，欢迎大家联系前来测试样品！