材料中材料流变光学检测方案(流变仪)

智能文字提取功能测试中

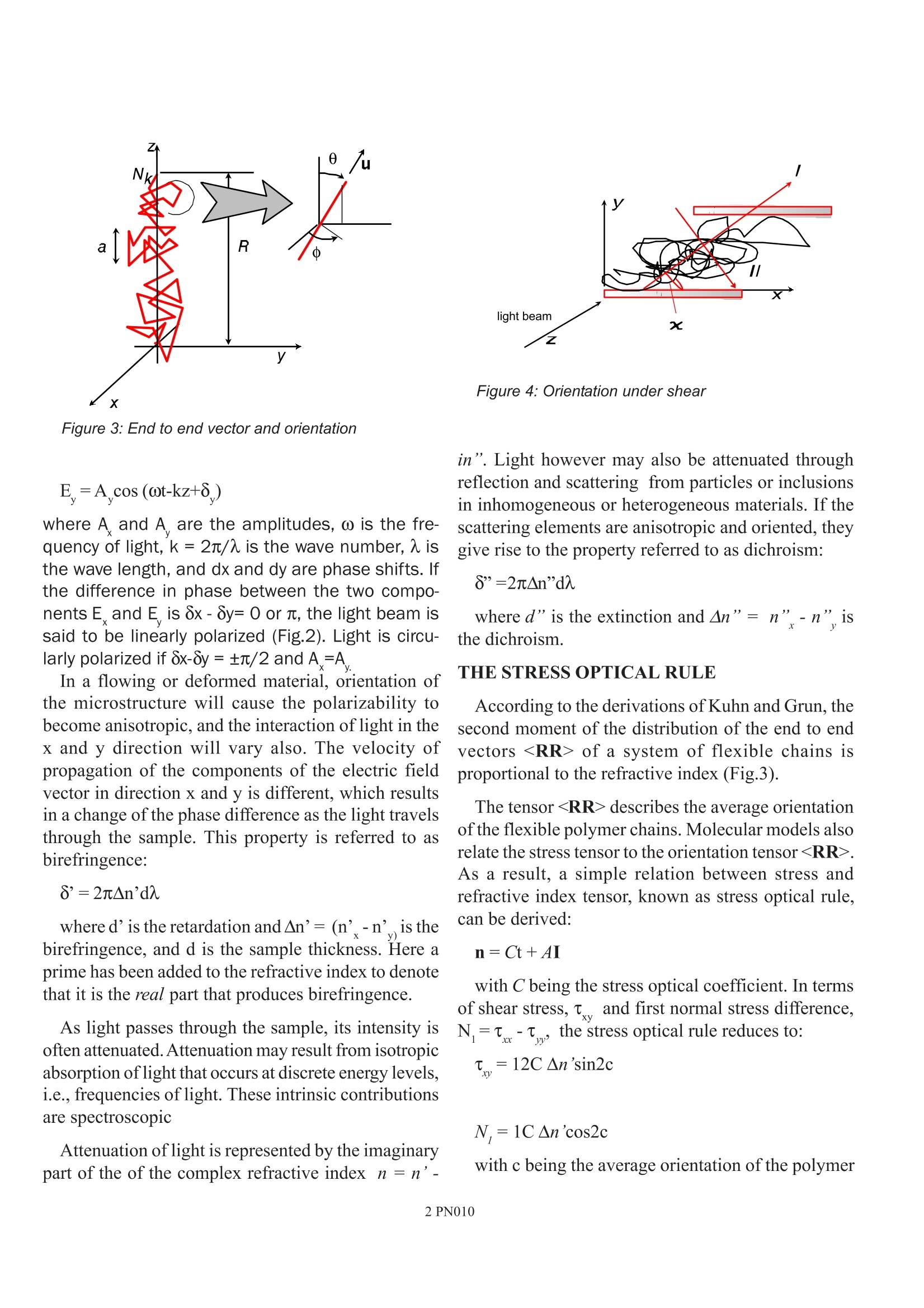
PN010 Rheo-optical measurements with the OAMII revised A.J. Franck， TA Instruments Keywords： polarimetry； dichroism； birefringance； refractive index； rheo-optics WHAT IS RHEO~OPTICS? Rheo-Optics refers to optical techniques applied todeforming systems to measure structure， orientationand stress. Optical measurements can be an importantcomplement to rheological mechanical measurementsas they can help to understand the mechanismscontrolling the flow properties exhibited by polymericand colloidal materials. The Optical Analyzer ModuleOAMII utilizes polarimetry， or the measurement oflight polarization， to determine anisotropy in therefractive index of materials subject to flow anddeformation. In contrast to rheometry， optical methodsdo not require contact with the material and focus on avery small volume of material. NATURE OF LIGHT& REFRACTIVE INDEX Figure 1： The electric field vector of light A beam of light may be thought as an oscillatingelectric field propagating through space. Whentraveling through matter， the electrically chargedelectrons and nuclei are affected by the electrical fieldand， as a result， the light beam is altered. This interactions is characterized by the polarizability ofthe material and causes the velocity of light to change.At the macroscopic level， this behavior is describedby the refractive index n， defined as the velocity oflight in vacuumc divided by the velocity of light inmatter. The refractive index is a scalar as long as themedium is isotropic. If light is traveling through acomplex anisotropic material， the refractive index willbe a complex tensor. POLARIZATION， BIREFRINGENCE ANDDICHROISM Light traveling along the axis z in space as a functionof time and distance is represented mathematically bythe electric field vector E and its two components inthe x and y direction (Fig.1)： Figure 3： End to end vector and orientation where A and A are the amplitudes，ω is the fre-quency of light， k=2n/ is the wave number， A isthe wave length， and dx and dy are phase shifts. Ifthe difference in phase between the two compo-nents E and E is 8x-8y=0 or n， the light beam issaid to be linearly polarized (Fig.2). Light is circu-larly polarized if 8x-8y=±/2 and A =A In a flowing or deformed material， orientation ofthe microstructure will cause the polarizability tobecome anisotropic， and the interaction of light in thex and y direction will vary also. The velocity ofpropagation of the components of the electric fieldvector in direction x and y is different， which resultsin a change of the phase difference as the light travelsthrough the sample. This property is referred to asbirefringence： where d’is the retardation and An’=(n’-n’is thebirefringence， and d is the sample thickness. Here aprime has been added to the refractive index to denotethat it is the real part that produces birefringence. As light passes through the sample， its intensity isoften attenuated. Attenuation may result from isotropicabsorption oflight that occurs at discrete energy levels，i.e.，frequencies of light. These intrinsic contributionsare spectroscopic Attenuation of light is represented by the imaginarypart of the of the complex refractive index n= n’- Figure 4： Orientation under shear in". Light however may also be attenuated throughreflection and scattering from particles or inclusionsin inhomogeneous or heterogeneous materials. If thescattering elements are anisotropic and oriented， theygive rise to the property referred to as dichroism： 8”=2元And where d”is the extinction and An”= n”- n”isthe dichroism. THE STRESS OPTICAL RULE According to the derivations of Kuhn and Grun， thesecond moment of the distribution of the end to endvectors of a system of flexible chains isproportional to the refractive index (Fig.3). The tensor describes the average orientationof the flexible polymer chains. Molecular models alsorelate the stress tensor to the orientation tensor As a result， a simple relation between stress andrefractive index tensor， known as stress optical rule，can be derived： with C being the stress optical coefficient. In termsof shear stress，T and first normal stress difference，N=T-， the stress optical rule reduces to： N，=1CAn'cos2cwith c being the average orientation of the polymer chains relative to the flow direction (Fig.4). The stressoptical rule enjoys wide validity for melts andconcentrated solutions of flexible chains. For large chain extensions (for example duringextreme elongational flow) the stress optical rule willfail due to saturation of the birefringence， while thestress is still increasing. The stress optical coefficientis dependent on the chemistry of the polymer (polarizability of the bonds between atoms and bondsin the direction of the backbone of the polymer) andthe solvent， but independent of molecular weight，concentration， and shear rate. Scattering and formbirefringence in heterogeneous and inhomogeneoussystems also cause deviations of the stress optical rule.These effects are not simply proportional to the secondmoment tensor. The stresses accessiblethroughh oopticalmeasurements depend on the direction， in which thelight travels in relation to the direction of the flow ororientation of a deforming or anisotropic material. Theconvention used here is shown in Fig. 4 where the flowis taken to be in the x direction， y is the gradientdirection， andz is the neutral direction. If the light beampropagates along the neutral axis z， shear stress andfirst normal force acting in the x-y plane can bemeasured. This is the case for Couette flow，where thelight beam enters through the bottom of the Couette. Ifthe light travels through a material in the directionofthe deformation gradient， only the third normal force(x-z plane) can be obtained. This is the case for shearflow in a cone and plate or a shear sandwich geometry，when then light beam is directed through a window inthe plate. BIREFRINGENCE AND DICHROISMMEASUREMENTS The optical train shown in Fig. 5 is used to measurebirefringence. With the circular polarizer removed，dichroism measurements can be made. The optical trainconsists of a solid state laser that generates awavelength of 670 nm， a polarizer fixed in position，followed by a rotating half wave plate spinning atQ=400 Hz. This produces linearly polarized light， thatspins at twice the frequency. The light is thantransmitted through the sample， held within a flow cell(normally two parallel quartz plates or a Couette cell). The light is analyzed with a circular polarizer anddirected to the detector for birefringence measurementsor directly send to the detector for dichroismmeasurements. In case that the system is set up for dichroismmeasurements， the light intensity at the photodetectorfor a birefringence and dichroism is given by： I=I (1-cos2ctanho"cos4Qt-sin2c tanh8"sin4t) with I the incident intensity. The signal of thephotodiode is sent to a signal conditioner， that alsoreceives signals from a modulation detector. Thisdetector produces a sinusoidal reference signal at thefrequency of the polarization modulation， 4Q. The timedependent signal produced by the samople detectorthat is given by the equation above is processed usinga lock-in amplifier that demodulates the signal. Thisresults in the following three Fourier coefficients： 'dc=1 lcos dc =-cos2x tanh8" 1 /1=-sin2x tanho" Once these three coefficients are known， theorientation angle， c， and dichroism An”， can becalculated. In the birefringence mode， with the circularpolarizer inserted between sample and detector， themeasured intensity signal is following： sin2ysin8']cos4Qt-[sin2ytanh8"+ cos2ysins8']sin4Qt) It should be noted， that the birefringencemeasurement is not independent of dichroism， whichhas to be taken into account if not negligible. Birefringence and dichroism data as a function ofapplied stress for a 6% polystyrene solution indioctylphtalate are shown in Figs. 6 and 7. The decreaseof shear rate above a stress of 300 Pa is due to adramatic increase of viscosity (shear thickening). Thedichroism changes sign at 300 Pa and its absolute valueincreases drastically. Since this solution does not absorb light， thedichroism is a direct measurement of shear inducedstructure， that scatter light. The change of sign reveals Figure 5： Optical train for birefringence and dichroisrnmeasurements that the orientation of the structure changes at the pointof shear thickening. The increase of birefringence isdue to a combination of intrinsic segmental orientationof the polymer chains and form effects due toconcentration fluctuations. In this example. dichroismis relatively more important f in understanding themicrostructural changes that cause the shearthickening. SIMULTANEOUS OPTICAL ANDRHEOLOGICAL MEASUREMENTS Simultaneous optical and mechanical measurementscan be used to study a wide variety of materials. *Determination of microstructure and dynamicsin block copolvmers. Multicomponent systems give rise to formbirefringence due to contrasts between refractiveindices of different phases. A block copolymer wellabove its ODT (order-disorder temperature)， wheremicro-domains exist can be expected to give rise tointrinsic birefringence. As temperature is loweredbelow the ODT， form effects occur and can often bereadily identified because form and intrinsiccontributions frequently are opposite in sign. * Determination of structure and dynamics ofsuspensions. When a suspension of particles becomes anisotropicupon shearing， it will show a dichroism due to the factthat light scattered by the sample will be independentof polarization. In a suspension of hard spheres， theonly mechanism to provide dichroism is the formation Figure 6： Birefringence for a PS solution in shearflow of anisotropy in the spatial arrangement of particles.If large clusters are formed， the relaxation time scaleof dichroism is expected to increase dramatically. Figure 7： Dichroism for a PS solution in shear flow *Measurement of structure and normal force insurfactants. Surfactants often follow the stress optical rule.Observed flow induced phase separations only affectthe normal stress. Birefringence measurements providea convenient and sensitive means to measure normalforce. PN Rheo-Optics refers to optical techniques applied to deforming systems to measure structure, orientation and stress. Optical measurements can be an important complement to rheological mechanical measurements as they can help to understand the mechanisms controlling the flow properties exhibited by polymeric and colloidal materials. The Optical Analyzer Module OAMII utilizes polarimetry, or the measurement of light polarization, to determine anisotropy in the refractive index of materials subject to flow and deformation. In contrast to rheometry, optical methods do not require contact with the material and focus on a very small volume of material.