现场总分析

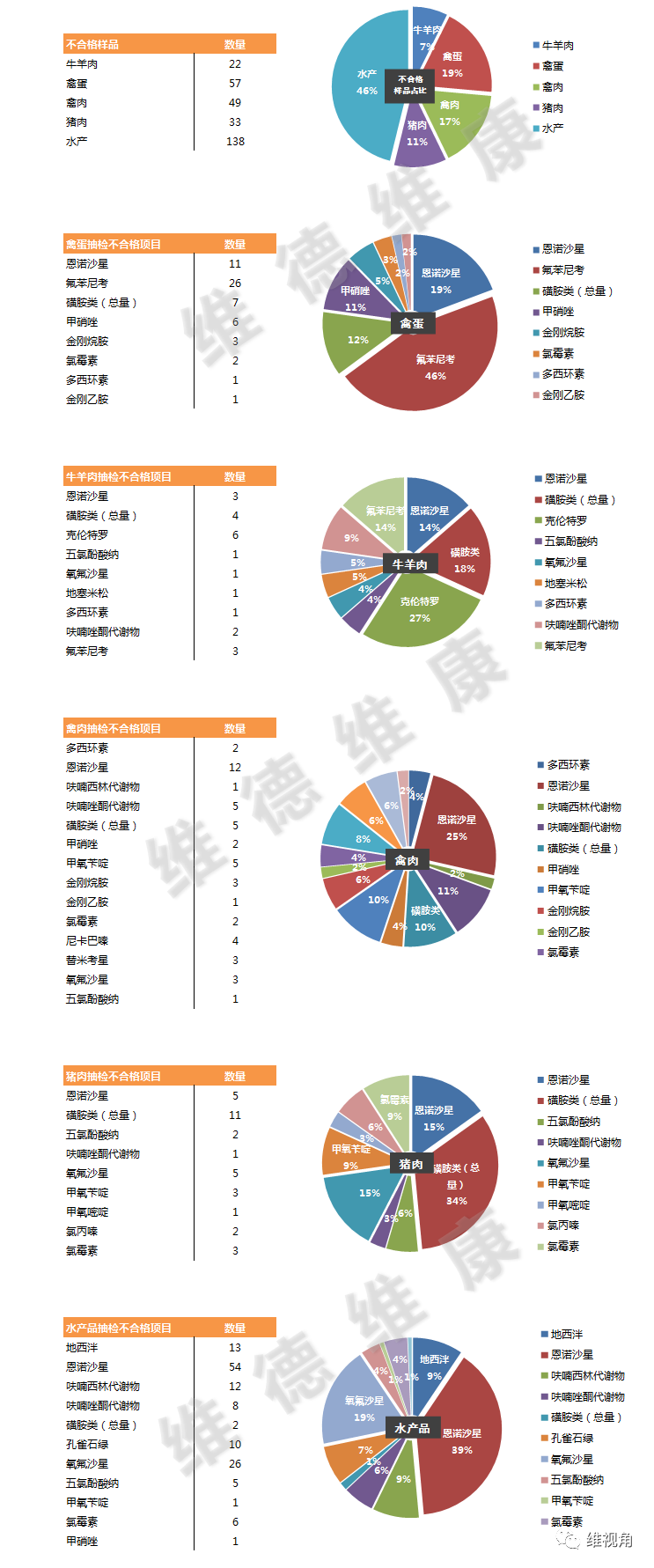
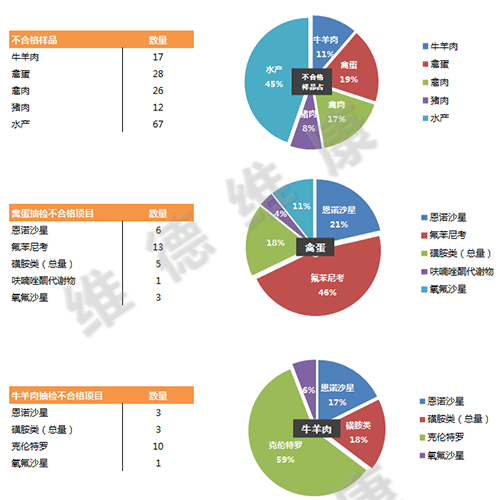
色谱柱效能指标n和柱的总分效能指标R有什么区别和联系

现场仪表系统的故障分析,一、现场仪表系统故障的基本分析步骤现场仪表测量参数一般分为温度、压力、流量、液位四大参数。现根据测量一、现场仪表系统故障的基本分析步骤现场仪表测量参数一般分为温度、压力、流量、液位四大参数。现根据测量参数的不同，来分析不同的现场仪表故障所在。1.首先，在分析现场仪表故障前，要比较透彻地了解相关仪表系统的生产过程、生产工艺情况及条件，了解仪表系统的设计方案、设计意图，仪表系统的结构、特点、性能及参数要求等。2.在分析检查现场仪表系统故障之前，要向现场操作工人了解生产的负荷及原料的参数变化情况，查看故障仪表的记录曲线，进行综合分析，以确定仪表故障原因所在。3.如果仪表记录曲线为一条死线(一点变化也没有的线称死线)，或记录曲线原来为波动，现在突然变成一条直线 故障很可能在仪表系统。因为目前记录仪表大多是DCS计算机系统，灵敏度非常高，参数的变化能非常灵敏的反应出来。此时可人为地改变一下工艺参数，看曲线变化情况。如不变化，基本断定是仪表系统出了问题 如有正常变化，基本断定仪表系统没有大的问题。4.变化工艺参数时，发现记录曲线发生突变或跳到最大或最小，此时的故障也常在仪表系统。5.故障出现以前仪表记录曲线一直表现正常，出现波动后记录曲线变得毫无规律或使系统难以控制，甚至连手动操作也不能控制，此时故障可能是工艺操作系统造成的。6.当发现DCS显示仪表不正常时，可以到现场检查同一直观仪表的指示值，如果它们差别很大，则很可能是仪表系统出现故障。总之，分析现场仪表故障原因时，要特别注意被测控制对象和控制阀的特性变化，这些都可能是造成现场仪表系统故障的原因。所以，我们要从现场仪表系统和工艺操作系统两个方面综合考虑、仔细分析，检查原因所在。

医学统计学是一门帮助人们透过偶然现象,分析和判断事物内在规律的科学。随着医学科研工作的深入,医学统计学的应用越来越广泛。由于统计学的内容非常丰富,并且仍在不断发展,而医务工作者常因各种原因不愿花费许多精力钻研统计学知识,故医学论文中误用统计学的现象较为严重。为了减少这一现象,提高论文的水平,现就论文中常见的统计学错误,分析讨论如下。1. 文中未交待所用统计方法论文中应将所用的统计方法交待清楚,例如,是配对设计的t检验还是成组设计的t检验,是Ridit分析还是卡方检验,是作相关分析还是作回归推断。使用不正确的统计方法会得出错误的结论,所以统计方法交待不清或根本不予交待,会使读者对论文结论的正确与否无法判断。有的作者只提一句“经统计学处理”后,就写出结论;有的甚至于直接用P值说明问题了事。正确的做法应写明具体的统计方法,如有特殊情况,还应说明是否采用了校正,这样才有说服力。严格地说,应写明精确的统计量值和P值,如t值、F值、χ2值等,不应笼统地以P0.05或P0.05代替。此外,最好能交待所使用的计算工具与统计软件名称。因采用公认的统计软件(如SAS、SPSS等)或程序型计算器进行计算,与手工计算相比,既准确又快捷,其计算结果易于被人接受。2. 使用统计方法时不考虑其应用条件每一种统计方法都有其适用条件。在表示数值变量资料(计量资料)的平均水平时常用到平均数。然而平均数有算术平均数(均数)、几何均数和中位数,各有其应用条件。应用均数时,必须首先确定数据为正态分布。如果数据是偏态分布,仍用均数表示其平均水平势必导致错误的结论,不少作者没有注意到这一点。对于偏态分布的数据,应该用几何均数或中位数表示其平均水平。t检验要求样本来自正态总体,作两样本均数比较时还要求方差齐。如果不符合这些条件,则应考虑进行数据转换或用非参数检验;当两小样本均数比较方差不齐时,可采用t’检验。例如临床研究中常涉及病人的病程,有的论文中病程5d至24年的平均水平和离散度为(311±613)年,这种标准差接近或大于均数的数据显然属于严重的正偏态,直接进行t检验,无疑是错误的。t检验是最常用的统计方法之一,但有许多误用的情况。t检验不能用于三组或三组以上的组间比较,即使资料符合t检验的条件也是不行的。因为一则将原来的多组整体设计割裂,失去了总变异和总剩余误差,与原设计思想不符;二则损失了部分信息,降低了检验效率。t检验误用于方差分析的现象还不少见。对于三组或三组以上组间的均数或分布的比较可以用以下方法:⑴如果各样本来自正态总体,且方差齐,可用方差分析;⑵如果各样本来自正态总体,但方差不齐,则可作数据转换,待方差齐后再用方差分析;⑶如果各样本分布不清或分布不明,则可考虑用秩和检验。在t检验中,把配对设计的资料作成组比较的t检验,是常见的失误之一。有的作者误将配对数据分为两个独立的组,分别设计两组各自的均数,并按两组均数作成组比较的t检验。这样使原来只有差值之间的变异扩大为“两个样本”各自的变异,错误地增大了标准差和标准误,同时样本含量也从原来的对子数变成了“两个样本”的例数之和。其结果大多使t检验所得P值增大,可导致差异从有统计学意义变为无统计学意义。卡方检验中的计算公式较多,各有其适用条件,稍有不慎,即有误用的可能,应根据实验设计和资料性质进行正确选择。常见的失误是:⑴四格表资料,当15,n(总例数)40时,没有计算校正χ2值;⑵四格表资料,当T1或n40时,没有选用四格表确切概率法;⑶行×列表资料,由于例数太少,致理论频数太小,没有采有适当的处理方法,而是直接计算χ2值,导致分析的偏性。例如两组共计15例,就不宜用一般的卡方检验公式计算,应该使用确切概率法。3. 统计学的基本概念不清楚在作统计推断时,对样本例数有一定的要求,一般认为,样本例数太少,所得到的数值不稳定,不能轻易下结论。有的论文中三组数据均为2例,便作出推断,其推断是不妥的。有一个常见的统计问题是多组间比较时的两两比较问题。统计学上,三组或以上的比较称为一揽子比较,在作这种比较时,应先将所有的组一起比较。在得出差别有统计学意义的基础上,再进一步作两两比较或多个处理与同一对照组比较。论文中常见的错误是将三组或以上组拆开分别作两两比较。正确的方法是:定量资料在方差分析P0.05后,再用Q检验或Dunnett法作两两比较;定性变量在R×C表资料χ2检验P0.05后,再作χ2分割法分析。对于有序分类资料(即等级资料)的统计处理,在比较各处理组的效应有无差别时,宜用秩和检验、Rid2it分析或交叉积差法及等级相关法,但有些作者则误用卡方检验,此时作卡方检验只能说明各处理组的效应在构成比上有无差异。部分作者对于“率”与“比”的概念不清,常将构成比误认为是发病率、患病率、死亡率。这三种率均为疾病统计指标,要做人群的流行病学调查才能得到。在临床疗效研究中,一般无法计算出这三种率。4. 相关回归分析中的问题相关分析是分析自变量x与因变量y的关系,医学领域里完全相关(相关系数r=1或-1)的事件极少,有作者将一组变量既作为自变量又作为因变量,r=1,认为有完全相关性,这说明对相关的概念还不十分清楚。不能把相关、回归关系直接看作因果关系。两事物间有数量关系,可能是因果关系,也可能不存在因果关系,而仅仅是伴随关系。如果求得了两个变量间数量关系的回归方程式,或算出了r,在做结论之前,应先作统计检验;若P0.05,此回归方程并无实际意义。r的实际意义如何,还要看r绝对值的大小,因r的统计学检验,不论P值多么小,只能提供两个变量是否相关的信息,却不提供相关是否密切的信息。相关的密切程度常以r的数值大小为指标。r的绝对值越接近于1,两变量的相关关系越密切;越接近0,越不密切。r的平方即r2(决定系数)也可表示因变量y与自变量x的关系密切程度,如果r2=0.22=0.04,说明因变量y的变异中仅有4%与x有联系;此时若P0.01,仍不能认为两者“明显相关”。5. 统计说法不严格统计学上对差异作是否有显著性意义的推断与日常生活中对差异作是否显著的推断完全是两个概念。主观感觉两个样本均数间的差异并不显著而统计学上作出差异有显著意义的推断,主观感觉两个样本均数间的差异很大而统计学作出其间差异无显著意义的推断都是有可能的。既往所用的“差异显著”、“差异非常显著”等字句,容易与日常生活判断的字句相混淆,故现在一般认为用“差异有或无统计学意义”较为清楚明白。对于假设检验的结果,不仅要恰当的解释、正确地分析,还要准确地予以表达。差异有无统计学意义,在检验水准α=0.05时,一般是以P0.05或P≤0.05为界线,有作者的结果为P0.01,由此判断差异无统计学意义,但P0.01不一定就是P0.05,也可能0.01 0.05,只有在P0.01同时也0.05,才能判断为差异无统计学意义。还有作者的假设检验结果为P=0.100000,虽然不能说是错误,可是不符合习惯用法。6. 数据统计的准确性文内所给出的各种数据及统计要准确无误,不能前后有别。有论文的文题是45例患者,而在统计表中相加为47例,但讨论中又说是46例,究竟是多少例患者似乎论文作者自己也说不清,只好退修;更有甚者,修改稿中数字错误更多。对于相对数,当例数较少时,一定要有相应的绝对数,如有的组只有4例,治愈2例,即报道治愈率为50%,这显然是不妥的。在计算构成比或有些率时,一定要注意合计必须是100%,有的时候因为四舍五入,合计为99.18%或100.11%,此时要作调整。严格地说,要按有效数字的运算法则“四舍六入,逢五前位奇进偶舍”计算。数据错误多,说明作者缺乏严肃认真的科学态度。7. 统计表不规范统计表的设计合理与否,对论文的质量和科学性有重大的影响。统计表存在的问题主要有⑴表题过于简略,甚至不写表题;或过于繁琐以及标题不确切；⑵标目过多,层次不清；⑶线条过多；⑷表内同一指标的小数位数不一致。表题应扼要说明统计表的内容, 一般不宜超过15个字。横标目说明各横行数字的涵义,纵标目说明各纵列数字的涵义,必要时在横、纵标目上可冠以总数目。通常把主语置于横标目,谓语置于纵标目。表的线条宜少勿多,常用三线表;除顶线、底线以及隔开纵标目与数字的横线外,其余线条均可省去,绝对不要用竖线,特殊情况下加辅助横线。表内数字一律用阿拉伯数字,同一指标的小数位数应一致,位次对齐。统计表强调以最小的篇幅说明最多的问题,避免一切不必要的线条与数字、符号和脚注,力戒繁琐,且勿堆累。若用简洁的文字已能说明问题,则尽量不用表。如用了统计表,则文中不宜再完全重复其数据,只需强调或描述其主要发现。同一资料,还要避免统计表与统计图之间的重复。总之,医学科研论文中所存在的统计学失误,大部分并非是深奥的数学问题,相当部分甚至是些统计学基础知识。只要我们加强医学统计学继续教育,打下扎实的医学统计学基础,就能减少统计学的失误,进一步提高论文的质量。