实验采集到的近红外光谱除包含与样本相关的有用信息外,往往也掺杂着干扰信息,包括随机噪声、背景干扰、杂散光及测样器件引起的光谱差异。这对定性或定量模型的质量和待测样本预测的准确度将产生严重的影响。因此,在用化学计量学方法建立模型之前,为了减小或消除光谱数据的噪声、散射的干扰和背景基线漂移等影响,有必要对光谱进行预处理。光谱预处理方法有很多,按照预处理效果,可以将预处理方法分为基线扣除、散射校正、平滑处理和尺度缩放四大类[18]。其中,每类预处理方法又包括多种具体算法。
一、背景扣除方法
光谱中除了组分的特征峰外,往往还存在连续、缓慢变化的背景,并且不同样本光谱的背景不同。背景的存在会使特征峰的峰位、峰宽以及峰的强度难以确定,并降低模型的解释性和稳健性。因此,扣除光谱中的背景很有必要。
1. 拟合或差值
对于给定的一些散点,拟合是用一个已知表达式而未知参数的连续函数来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续函数来穿过这些点。拟合和差值都可以对某些点进行估计。但插值没有误差,一定经过给定的点;而拟合有误差,不一定过给定的点,更多的是在表现数据的趋势。进行拟合或插值的连续函数可以是线性函数、多项式函数或样条函数等。
用拟合或插值进行背景扣除分为手动形式和自动形式两种。手动形式就是从原始光谱中挑出一些认为是背景的点,然后再进行拟合或插值,得到背景曲线,从原始光谱中扣除背景即达到背景扣除的目的。手动方法的精确度依赖于工作者的经验,并且不具有可重复性,由此发展了自动拟合或插值的方法。去趋势(de-trending)[19]就属于自动扣除背景的方法。该类方法在信噪比或者背景较小的情况下能取得较好的效果,但是对于高信噪比或背景复杂的光谱不能取得满意的效果。
2. 导数计算
光谱的一阶(1st derivative)和二阶导数(2nd derivative)是常用的背景扣除方法[20]。一阶导数可以简单用一阶差商代替,即相邻两点的差值除以相邻采样点的间隔。二阶导数可采用一阶导数继续求导获得。一阶导数主要解决基线的线性偏移,高阶导数则解决基线的非线性漂移。导数光谱在消除基线和其他背景干扰的同时也会带来噪声的增强,因此,可以在求导前先进行平滑处理。
常用的导数计算方法包括直接差分法、Savitzky-Golay(SG)求导和Norris-Williams(NW)求导。直接差分法就是用后一个光谱点与前一个光谱点依次作差,对于分辨率高的光谱,直接差分法得到的导数光谱与实际相差不大;但对于稀疏波长采样点的光谱,该方法所求的导数则存有较大误差,此时可以用SG求导。SG求导方法是将移动窗口多项式拟合进行求导,利用导数取代窗口的中心点,窗口每次只移动一个数据点,直到整个光谱的数据点都得到了求导的结果。与SG平滑一样,窗口宽度是SG求导中需要确定的一个重要参数。NW求导是由Norris于1983年提出的,该方法首先进行光谱的平滑,然后根据给定的窗口宽度和窗口间隔对平滑后的光谱进行一阶或二阶求导。窗口间隔是指两个窗口之间波长点的间隔。
3. 小波变换
小波分析是20世纪七八十年代基于Meyer、Daubeichies和Mallat等人奠基性工作而发展起来的一种数据分析方法,具有时频分析的特点,又被称为“数学显微镜”。小波分析的目标是用一组基函数及其变换,对原始信号给出丰富有效的描述。这些基函数就是由母小波通过尺度伸缩和位置平移扩展出来的一系列函数。在使用小波前首先要选定小波函数及小波参数等。小波变换(WT)就是将信号从原始空间通过基函数投影到小波空间,包括离散小波变换(Discrete wavelet transform, DWT)和连续小波变换(Continuous wavelet transform, CWT)。小波变换在分析化学的数据处理中得到了广泛应用[21],包括平滑滤噪、数据压缩、背景扣除、基线校正、分辨率提高、峰的校对等方面。
DWT将原始信号逐层分解为低频和高频信号。高频信号不作处理,而对低频信号持续进行分解。一般认为,分解后的高频信号一般为噪声信息,低频信号为背景信息。因此,DWT可以用于噪声和背景的扣除。CWT通过基小波位置平移或尺度伸缩,把一维信号扩展成二维信号。由于小波基函数可以认为是某平滑函数的导数,因此CWT可以看作是近似求导的过程,从而能达到扣除背景的目的[22]。
4. 峰位寻找-峰宽确定-拟合或差值三步法
以上背景扣除和基线校正的方法各有优缺点,人工拟合或插值需要借助经验,并且比较费时;自动拟合或插值在信噪比低或背景强时效果会很差;导数计算的方法会使峰的形状改变,难以对预处理后的谱峰进行解释;DWT的方法是假设背景、噪声与信号完全分离,去掉代表低频的背景,然而实际信号并非都可以完美分离。峰位确定、峰宽寻找、拟合或插值三步法可以结合以上方法的优点,为基线扣除提供了一种智能化的方法。Baek等[23]将SG平滑用于峰位的确定和峰宽的寻找,然后用插值确定背景。该方法应用于模拟光谱和真实样本的拉曼光谱。结果显示,该方法可以有效地去除模拟信号中的直线和曲线背景以及拉曼光谱中的背景。但是复杂背景的存在往往会影响峰位的确定,张等[24]充分利用小波变换的优势,把光谱转换到小波空间,再在小波空间寻找峰位。首先以墨西哥帽小波为母小波对拉曼光谱进行连续小波变换。根据小波系数的局部极大值来确定峰的位置,然后通过哈尔(Haar)小波变换导数计算来确定峰的宽度;最后,将光谱信号分为峰部分和非峰部分,非峰部分使用惩罚最小二乘拟合,从原始光谱扣掉拟合后的背景得到校正背景后的光谱。该方法可以很好地校正拉曼光谱的背景而无需对光谱进行任何预处理。
5. 自适应迭代不对称惩罚最小二乘法
用于平滑的惩罚最小二乘和不对称最小二乘虽然也可以用于背景扣除,但是用于复杂信号时容易产生负峰。张等[25]提出了自适应迭代加权惩罚最小二乘(airPLS)的背景扣除方法。此方法的实质是通过迭代过程优化一个包含两项的目标函数。第一项为扣除背景后的光谱的不对称最小二乘,用于计算拟合误差;第二项为拟合背景的一阶导数,用来限制背景的平滑程度。结果表明,该方法能有效地扣除模拟光谱、高效液相色谱和拉曼光谱信号中的背景,且计算速度很快。
二、散射校正方法
即使是相同的样本,但由于样本粒度大小的不均匀分布,多次测量的样本也会出现差异,此时需要散射校正的方法对其进行校正。散射校正包括标准正态变量(Standard normal variate, SNV)、多元散射校正(Multiplicative scatter correction, MSC)和辐射转移公式(Radiative transfer equation, RTE)。
1. 标准正态变量变换
标准正态变量(SNV)[19]用来校正样本中因颗粒散射、光程变化而引起的光谱误差。SNV认为每条光谱中各波长点的吸收度值应满足一定的分布(如正态分布),利用这一假设对每条光谱进行校正,即从原始光谱中减去该光谱的平均值后,再除以该光谱的平均偏差。经过SNV处理后的光谱矩阵每行元素均值为0,方差和标准偏差都为1。显然,SNV使信号的强度和尺度得到调整,从而达到散射校正的目的。SNV与标准化算法的计算公式相同,不同之处在于前者对光谱阵的行进行处理,不需要对性质数据同时处理;后者基于光谱阵的列,光谱与性质数据需同时处理。
2. 多元散射校正
多元散射校正(MSC)由Geladi等[26]在1983年提出,用于消除由于样本颗粒分布不均匀及颗粒大小不同产生的散射对其光谱的影响。MSC假定所有样本在各波长点具有相同的散射系数,并且每条光谱都应该与“理想”光谱成线性关系。显然能代表所有样本的理想光谱并不存在,一般用校正集的平均光谱来代替。因此,MSC算法中首先计算所有光谱的平均光谱,然后用最小二乘回归算法构建线性回归方程,拟合每条光谱与平均光谱的关系,最后从每条光谱中扣除其截距并除以其斜率,得到校正后的光谱。对于校正集外的光谱进行MSC处理时,则需用校正集样本的平均光谱先求取该光谱的截距和斜率,再进行MSC变换。MSC与SNV具有一定的相似性。由MSC的算法可知,它主要用于消除理想中的线性散射影响。
3. 辐射转移公式
体系的散射与粒子粒径大小有很大关系。对于均匀体系,比如溶液等,光透过时,不存在散射问题,如图5-4 (a) 所示。对于非均相体系,若粒子的浓度很低,主要存在粒子本身的散射,不存在不同粒子之间对光的折射,如图5-4 (b)所示。若粒子的浓度较高,粒子之间对光的传播也会产生影响,如图5-4 (c) 所示。SNV和MSC在散射较大且目标分析物的浓度较小时不能取得很好的效果。为解决低浓度粒子引起的散射问题,Thennadil等[27]在2009提出了基于辐射转移理论(RTE)的散射校正方法,并用于两组分及多组分体系。
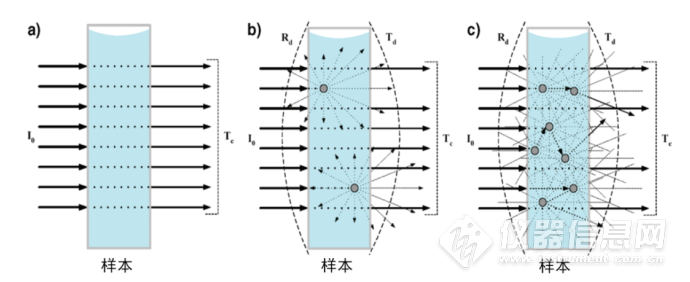
图5-4不同体系的溶液中散射情况示意图(a)匀质粒子;(b)低浓度粒子;(c)高浓度粒子
三、噪声去除方法
由于受温度、机械以及电磁等影响,光谱仪器产生的信号往往包含噪声。噪声的存在会降低信号分辨率,掩盖有效信号,降低建模的准确性。因此在进行光谱信号分析之前通常需要去噪。目前常用的去噪方法可以分为两大类:基于平滑和分解的去噪方法。前者包含移动窗口平滑去噪、Savitzky-Golay平滑。后者包含傅里叶变换(FT)、小波变换(WT)、经验模态分解(EMD)去噪。
1. MW平滑
移动窗口(MW)平滑是一种最简单的数据平滑方法。具体为将数据分割为具有一定宽度的窗口,将窗口内所有数据的平均值代替原始数据中窗口中心位置的数据的方法。采用MW平滑方法无法对数据两端半个窗口宽度范围的数据进行处理,可能导致该位置的光谱断裂。针对该情况可以采用将光谱数据向两端延拓的策略改善。
该平滑过程可表示为原始数据与长度为n的向量[1/n, 1/n, …1/n]T进行卷积操作。可以看出该向量为一个典型的低通滤波器,能够抑制频率较高的噪声成分。
2. SG平滑去噪
Savitzky-Golay(SG)平滑是一种改进的移动窗口数据平滑方式,其特点是窗口中心的数据具有更大权重,边缘位置权重较小加权移动窗口平滑方式。SG系数是通过多项式拟合的方式推导出来的,具体为:将窗口内的数据表示为特定阶数的多项式,通过最小二乘的原理可以求解多项式系数,基于拟合的函数可以求得原始信号的平滑结果及其高阶导数。
3. 小波变换分解去噪
小波变换包含离散小波变换(DWT)和连续小波变换(CWT),不仅具有背景扣除功能,也具有去噪功能。DWT通过对原始信号的不断分解,得到一个近似(Approximation)与多个细节(details)信号。近似信号即低频信息;细节信号即高频信息。将高频信息的噪声去掉,剩余的近似和细节信号重构为去噪后的信号。连续小波变换是原始信号与小波信号的卷积,同时具有平滑和求导的作用。
4. 经验模态分解去噪
经验模态分解(EMD)[28]是一种适用于非线性、非平稳信号的自适应分解方法。与小波变换相比,该方法不需要选择小波函数以及分解尺度。具体分解过程如图5-5所示,通过寻找原始信号极大值、极小值,上下包络线,计算平均包络线,作差值等步骤进行自适应分解。得到一定数目的按照频率从高到低的本征模态函数(Intrinsic mode functions, IMFs)和残差。所有IMFs和残差的加和等于原始信号。因此,将代表噪声的频率IMFs去掉,剩余IMFs和残差加和就得到去噪后的光谱信号。
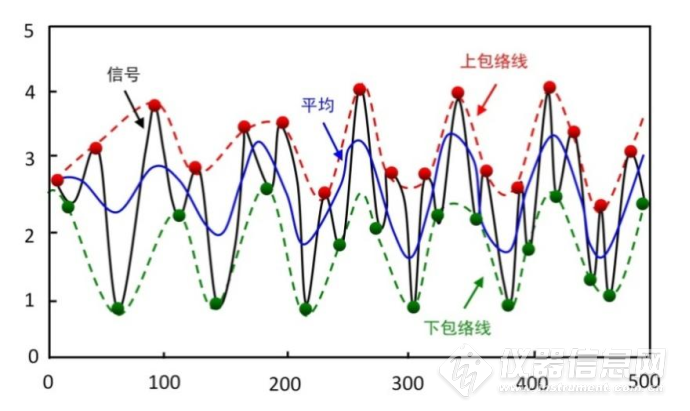
图5-5 经验模态分解过程示意图
四、尺度缩放方法
1. 数据中心化
数据中心化(Centralization)是从每个光谱数据中减去所有样本光谱的平均值,使得数据的变化以平均值为原点,从而充分反映光谱的变化信息,可以简化并稳定下一步的回归模型的计算。
2. 数据归一化
数据归一化(Normalization)是把量纲不同、范围各异的数据变为(0-1)之间无量纲的数据。数据归一化包括最大归一化、最小归一化、最大最小归一化和平均值归一化等。其中,最大最小归一化是常用的一种归一化形式,该方法将原始光谱矩阵的各个数据减去该数据所在列的最小值再除以该列数据的极差(最大值和最小值之差)。
3.数据标准化
数据标准化(Standardization)又称为均值方差化或方差归一化,用每列数减去该列数的平均值再除以该列的方差。经过标准化处理后的光谱矩阵每列元素均值为0,方差和标准偏差都为1。如果不同光谱同一吸光度下的波长变量之间数据差异较大,则需进行标准化处理。该方法既可以消除由于样本颗粒不均匀所带来的影响,也可以消除单位不同带来的影响。



