原子吸收中 积分吸收 和 峰值吸收 的概念

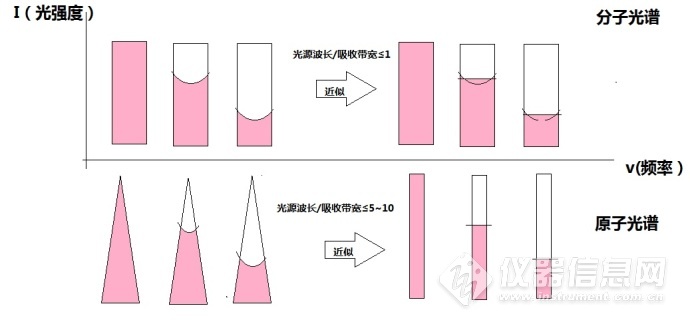
个人理解就是 当发射线宽度/吸收线宽度＜5~10时，可以近似认为 1.高斯分布的 I-v图近似认为是矩形分布，即I=C（常数）2.吸收线为水平线，而不是凹面
与分子光谱的不同之处在于，紫外—可见光谱的I-v图本身就是I=C（常数)，只需要发射线宽度/吸收线宽度＜1即可近似认为凹面吸收线为水平线。
汇总就是，原子吸收和分子吸收本质上都做了近似，当“发射线宽度/吸收线宽度＜1”时，可近似认为在中心线?△v范围内，吸收系数为常数；当“发射线宽度/吸收线宽度＜5~10“时，除了可以做上面的假设，还可近似认为发射线在中心线?△v范围内，光强度不随v变化。

非常抱歉，很多专业术语用的不是很严谨，加上脑子有点不清晰，但这就是在思考分子光谱法和原子光谱法光源要求的区别时，想到的内容。

应助工程师

原子吸收是动态测试，吸收系数不是一个固定值，

一般是积分吸收

其实我是理解不了教科书上 利用 经典色散理论中的 积分吸收 和 峰值吸收 推导 定量关系的内容
基本原理就是 Lamber-Beer定律吧，该定律在1852年就正式提出，有很多前提条件：
其中重要一条就是 摘自Wiki
“The incident radiation should preferably be monochromatic, or have at least a width that is narrower than that of the attenuating transition. ”
发射光必须为单色光，或者至少发射光谱宽度小于吸收宽度。
那就很容易理解了，就拿火焰原子吸收为例，吸收线半峰宽约为0.005~0.01nm，假设原子化效率和雾化效率恒定，则基态原子数正比于溶液中元素浓度，这里Beer定律中的溶液浓度就为火焰中基态原子的浓度。但为了满足定律要求，光源谱宽必须小于吸收线半峰宽，但普通光源（钨/氘） 单色器无法得到“小于吸收宽度”的光谱，故催生了空心阴极灯的产生（约为吸收宽度的1/10）。
问题是这中间没有和经典色散公式 和 峰值吸收 扯上半毛钱关系，L-B定律就解决了，不知道那两个公式在书上占据那么大的篇幅，意义何在？

额，突然想到，这难道就是 Lamber-Beer定律 前提条件“单色光或者小于吸收宽度的光谱” 的 内在机理？

刚扫了一眼 Walsh 1955发表的文章“The application of atomic absorption spectra to chemical analysis”
貌似教科书上的内容是摘自该文章，很奇怪的是，Walsh在1955年并没有直接引用 Beer定律，而是引用的Lambert定律，也就是 光强度 与 吸收光程 的关系，最后结合经典色散理论，进一步推导 吸光度 和 原子浓度 的关系，难道Beer定律提出时，有一定的使用限制？

应助达人

原吸理论理解起来很费力，但对大家的讨论很感兴趣，伫立旁观中。。。