


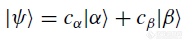
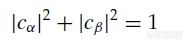
tcxuefeng
第2楼2012/08/25
说一下角动量的引入。
为了描述分子在三维空间随时间的自由旋转运动,我们采用了如下方程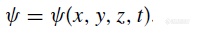
其中x,y,z是空间坐标,t为时间变量。而围绕此方程,我们引入了角动量算符*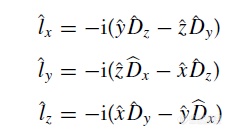
其中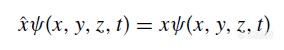
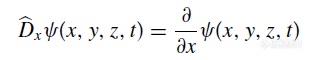
y,z同样。上面算符的给出我们并没有必要去深究,重要的是通过推导,我们发现了如下的规律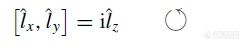
只需稍加变换,我们围绕角动量算符定义了旋转算符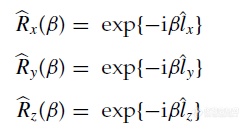
旋转算符的意义在于,它规定了向量在空间的旋转。其中x,y,z为旋转所围绕的轴,β为围绕此轴向量旋转的角度。举例说明,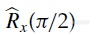 代表的是围绕+x方向90度的旋转(如下图)
代表的是围绕+x方向90度的旋转(如下图)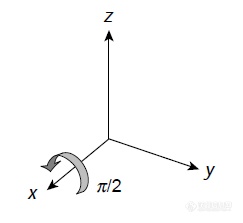
大家可能会好奇,是什么围绕x方向旋转呢?这正是算符的特殊之处——它只是规定的一种物理变换,就像加减乘除一样,本身没有任何取值。但是如果我们在其后面跟上一个实际物体空间坐标方程ψ(x,y,z,t),那么这一旋转就有了”依靠“。
*注:使问题从一种状态变化为另一种状态的手段称为操作符或算符。在物理学里,算符是一个函数,作用於物理系统的物理态 (physical state),使这个物理态变换为另外一个物理态。
tcxuefeng
第3楼2012/08/25
为什么要引入算符系统对量子系统进行描述呢?因为大部分情况下我们无法得到精确描述原子核的方程,但是我们却欣喜的发现,这些自旋核所处的状态是有规律可循的,通过一些外界变换(算符),我们可以直接”看“到自旋核的最终状态。就好像生活中我们可以自由控制身体来完成各种动作,却不必关心也无从知晓控制这些行为的生化反应过程一样。
为了区别前面广义的角动量算符,我们以符号I代替前面的L来描述自旋核的角动量。同样地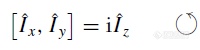
而对于任意自旋数为I的核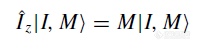
其中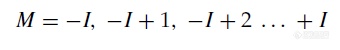
对于1/2核而言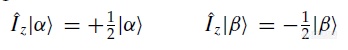
可见,对于|α﹥和|β﹥,Iz这一算符并不会对|α﹥和|β﹥所处的自旋状态带来任何影响(事实上±1/2被称作特征值,所描述的是这一系统所处的能量状态)。但是另外两种算符却会对系统自旋状态产生影响
其中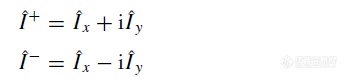
通过数学变换,我们最终可以将这些抽象的算符表示用矩阵形式来替代。对于1/2核而言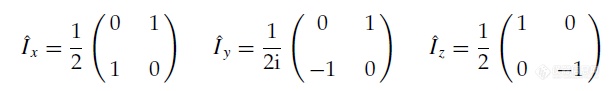
而它们各自所对应的旋转算符为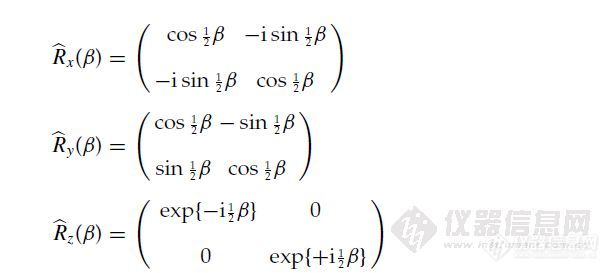
以上即为1/2核角动量算符及旋转算符的矩阵表示,将被大量应用到我之后对于核磁各种现象的描述中来。