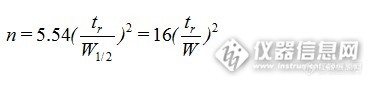色谱柱分析时，标样和样品的峰都随时间加宽，是否正常？

原因
一般来说，如果保留时间没有很大区别，只是加宽的峰拖尾，可能表明有活化点。如果加宽的峰是对称的，可能是由于正常的色谱柱“损耗和流失”。如果峰前伸，说明色谱柱过载。
这一问题需要从色谱的塔板理论进行解释。塔板理论是色谱学的基础理论，塔板理论将色谱柱看作一个分馏塔，待分离组分在分馏塔的塔板间移动，在每一个塔板内组分分子在固定相和流动相之间形成平衡，随着流动相的流动，组分分子不断从一个塔板移动到下一个塔板，并不断形成新的平衡。一个色谱柱的塔板数越多，则其分离效果就越好。
塔板理论是Martin和Synger首先提出的色谱热力学平衡理论。它把色谱柱看作分馏塔，把组分在色谱柱内的分离过程看成在分馏塔中的分馏过程，即组分在塔板间隔内的分配平衡过程。塔板理论的基本假设为：
①色谱柱内存在许多塔板，组分在塔板间隔（即塔板高度）内完全服从分配定律，并很快达到分配平衡。
②样品加在第0号塔板上，样品沿色谱柱轴方向的扩散可以忽略。
③流动相在色谱柱内间歇式流动，每次进入一个塔板体积。
④在所有塔板上分配系数相等，与组分的量无关。
虽然以上假设与实际色谱过程不符，如色谱过程是一个动态过程，很难达到分配平衡；组分沿色谱柱轴方向的扩散是不可避免的。但是塔板理论导出了色谱流出曲线方程，成功地解释了流出曲线的形状、浓度峰值的位置，能够评价色谱柱柱效。
解决方案
根据塔板理论，待分离组分流出色谱柱时的浓度沿时间呈现二项式分布，当色谱柱的塔板数很高的时候，二项式分布趋于正态分布。则流出曲线上组分浓度与时间的关系可以表示为：

这一方程称作流出曲线方程，式中Ct为t时刻的组分浓度；C0为组分总浓度，即峰面积；σ为半峰宽，即正态分布的标准差；tR为组分的保留时间。
根据流出曲线方程人们定义色谱柱的理论塔板高度为单位柱长度的色谱峰方差：

理论塔板高度越低，在单位长度色谱柱中就有越高的塔板数，则分离效果就越好。决定理论塔板高度的因素有：固定相的材质、色谱柱的均匀程度、流动相的理化性质以及流动相的流速等。
由流出曲线方程，经推导，可得出色谱峰宽W与理论塔板数之间存在关系：

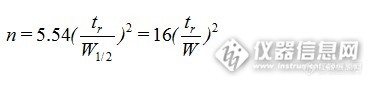
由这一公式可以得出如下结论：
a.在色谱柱不变的情况下，即理论塔板数n和长度L都不变的情况下，色谱峰宽度与保留时间t成正比。或者说：同一次分析里，色谱峰的宽度与其保留时间成正比。因此出峰越晚，峰宽越大。
b.在理论塔板数n不变的情况下，峰高与保留体积（时间）t成反比。或者说：同一次分析中，同样浓度的不同组分，出峰越晚峰高越小。
c.在色谱柱加长的情况下，理论塔板数n和保留体积（时间）t都同时等倍增加，因此色谱峰宽与色谱柱长度的平方根成正比。即色谱柱长增加一倍，峰宽增加到原来的1.414倍。还记得柱长增加一倍，保留时间差增加多少么？这是速度方程的结论，增加一倍。因此分离度R在柱长增加一倍的情况下，只能增加到原来的1.414倍。即：理论塔板高度H不变的情况下，分离度R与柱长的平方根成正比。
d.在色谱柱长度固定的情况下，即保留时间相等的情况下，色谱柱宽度W与理论塔板数n的平方根成反比。这意味着：在同样长度的不同色谱柱上，柱效率n越高，色谱峰越尖锐。通常理论塔板数n即柱效率n，但有时也把单位柱长下理论塔板数称为柱效率。由于毛细管具有极高的柱效，因此同样分析时间下，可以看到毛细管色谱峰明显要尖锐的多。
e.色谱峰高与组分总进样量m成正比。因此在进样体积一定的情况下，峰高与组分浓度c成正比，因此峰高可以用来定量。但峰高还会受到保留时间、理论塔板数n等影响，特别是当色谱峰形不正常，塔板理论不完全成立的时候，这个关系会受到影响，因此通常不用峰高定量。色谱峰面积都和进样量成正比，因此任何时候都能用峰面积定量。只有在峰形良好且尖锐的情况下，用峰高定量比较简单。
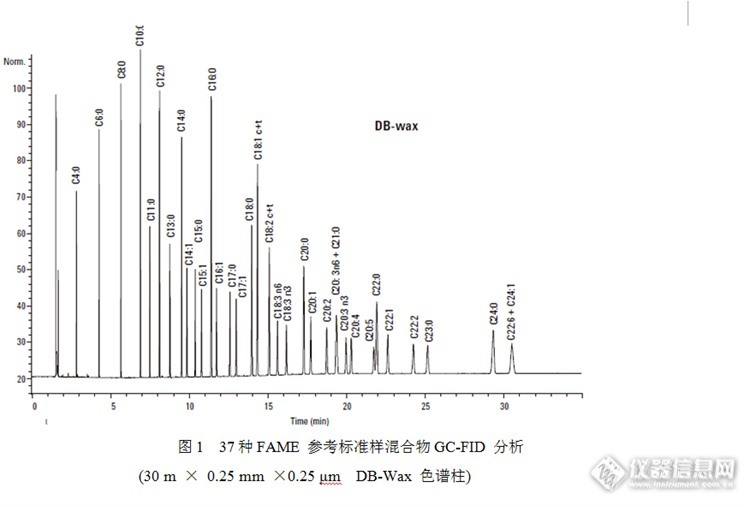
(4)案例分析
在DB-Wax 柱上分析37 种组分FAME 参考标准样的典型色谱图，如图1所示。从图中可以看出，样品的峰随保留时间延长而明显加宽，而且色谱峰的峰高也有明显下降趋势。

22323