中文摘要: 目的 通过近红外光谱技术对组分IV上清液酸沉过程中人血白蛋白的含量进行测定,实现酸沉过程人血白蛋白含量的过程监测。 方法 在实验室条件下模拟8批酸沉过程,以溴甲酚绿(Bromocresol Green, BCG)比色法测定人血白蛋白的含量;然后以5批作为校正集,3批作为验证集,建立人血白蛋白含量的PLSR定量测定模型。 结果 对变量选择方法进行了详细考察,最终选择35个有效变量建立模型,得到的模型Rc2、Rp2、RMSECV和RMSEP分别为0.977、0.978、0.7038 g/L和0.5893 g/L。 结论 评价结果显示模型有较好的预测能力,可用于酸沉过程中人血白蛋白的含量测定。
关键词:近红外光谱分析技术;组分IV;化学计量学;酸沉淀
人血白蛋白(Human Albumin,HA)是最早从人血浆中提取并应用于临床上的血液制品。在人血白蛋白(Human Albumin, HA)生产过程中,需要对FIV上清液进行酸沉,其目的为酸性条件下使HA沉淀下来,得到FV的沉淀,为下一步HA产品的纯化和精制做准备。在制药领域,NIRS作为一种重要的PAT工具,已成功用于药物的原辅料质量评价、关键过程的监测和控制、成品的快速放行和质量检测等各个环节,为保证产品质量、降低生产成本、革新生产过程发挥了重要的作用。本研究将PAT的理念引入到生产过程,对酸沉过程中HA的含量进行实时监测,根据HA的含量的变化即时调整醋酸缓冲液的加入速度,在保证产品的质量的同时提高生产效率。
1 材料
1.1 试剂
FIV压滤后上清液(山东泰邦生物制品有限公司);pH 4.0的醋酸缓冲液(山东泰邦生物制品有限公司);白蛋白检测试剂盒(美国BioAssay Systems公司);去离子水。
1.2 仪器和软件
Antaris II FT-NIR光谱仪(美国Thermo Fisherscientific公司);内径4×50 mm的玻璃小管(Kimble Chase,德国);低温反应仪(郑州长城科工贸有限公司);离心浓缩仪(Thermo Fisher Scientific公司);高速离心机(Thermo Fisher Scientific公司);酶标仪(Thermo Fisher Scientific公司);MATLAB 2013b(美国Mathworks公司);PLS_Toolbox工具箱(美国Eigenvector Research公司)。
2 方法
2.1 酸沉过程
实验室条件下模拟8批酸沉过程,反应在低温反应仪中进行,温度设置和实际生产相一致。具体过程如下:取100 mL FIV压滤后上清液置于圆底烧瓶中,然后将圆底烧瓶置于温度恒定的低温反应仪中;酸沉过程开始前取样1 mL后开始滴加醋酸缓冲液(pH4.0),醋酸缓冲液的加入方式为前9次每次加0.2 mL,后6次每次加0.8 mL;酸沉过程中每4 min加一次醋缓并取样1 mL并做离心处理,用于光谱的采集和HA含量的测定,每个酸沉过程得到16个样品。
2.2 样品光谱的采集
Antaris II FT-NIR光谱仪的透射模块进行原始近红外光谱的采集。光程4 mm,光谱范围10000-4000 cm-1,分辨率为8 cm-1,扫描次数32;每小时采集一次背景,以空气作为参考。所有样品采集3张原始光谱,以平均光谱作为最终的样品光谱。
2.3 白蛋白含量的测定
HA含量的测定方法为BCG法,采用市售的试剂盒进行测定。为了去除样品中乙醇对HA含量测定的影响, HA含量测定前通过离心浓缩仪将溶剂去除,然后去离子水复溶。含量测定的具体步骤如下。
标准曲线的制作:
① 将50 g/L的牛血清蛋白标准品用不同量的蒸馏水稀释,得到牛血清白蛋白含量在0-40 g/L范围内的标准品溶液;
② 向96孔板中加入5 μL不同浓度含量值的标准品溶液,然后加入200 μL试剂并轻敲孔板使其混合,使每个板孔中不要留有气泡;
③ 室温下静置5 min,利用酶标仪在630 nm处读取吸光度值;
④ 根据得到的吸光度值和标准品的浓度值拟合用于测定HA含量的标准曲线。
样品的测定:
① 向96孔板中加入5 μL的待测样品,然后加入200 μL试剂并轻敲孔板使其混合均匀,并将板孔中气泡赶出;
② 室温下静置5 min,利用酶标仪于630 nm处读取吸光度值;
③ 根据得到的吸光度值代入拟合的标准曲线中,算得样品的HA含量值。
2.4 数据的处理和模型的建立
研究中利用MATLAB 2013b 数学软件以及基于该软件的PLS_Toolbox工具箱对光谱数据进行处理,建立酸沉过程中HA含量测定的PLSR定量分析模型。首先将8批样品中的5批样品作为校正集,剩余的3批作为验证集;然后对光谱进行预处理和变量选择,以提取光谱的有效信息,得到稳健性和准确性高的定量模型;最后对模型进行验证和评价。在模型的建立中以留一法作为交互验证方法。为得到最佳的模型结果,本研究中引入缩小浓度区间的策略。
3 实验结果
3.1 样品原始光谱
本实验中平行进行了8个批次的酸沉过程,每个批次收集16个样品,共得到128个样品。图1为128个样品的原始近红外光谱图,。
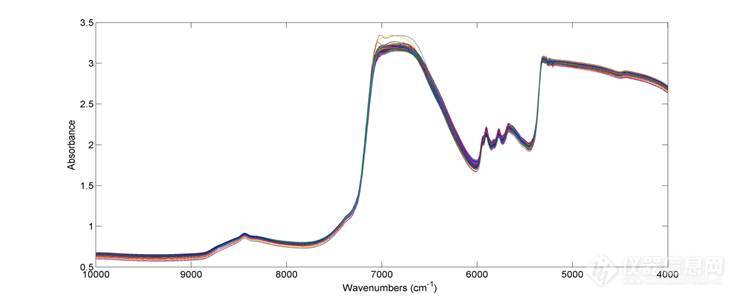
图1 酸沉过程原始光谱
3.2白蛋白含量测定结果
采用白蛋白检测(BCG法)试剂盒进行HA含量的测定,每次含量测定前进行标准曲线的建立,并保证R2在0.99以上。拟合的曲线类型为y=a*x/(b+x),测定范围为0.1-40 g/L。
测得的8批HA含量的结果如图2所示。由图中显示,在酸沉的开始阶段HA的含量变化不太明显;第5个取样点至第11个取样点HA的含量变化较为明显,出现急剧下降的趋势;第11个点之后HA的含量变化又趋于平缓,基本不再发生变化。由此可见,在第5至11个取样点间为主要的沉淀阶段,此阶段大量溶于溶剂中的HA沉淀下来,同时其它杂蛋白也有可能以共沉淀的形式沉淀下来。因此需要对酸沉过程进行实时监测,在HA沉淀较慢阶段可适当放大加酸速度,在沉淀下降较快阶段放缓加酸的速度,以便在得到最纯的HA沉淀的同时尽可能缩短酸沉淀的时间,一方面可以提高生产效率,一方面缩短HA在酸醇环境的时间,减少失活的可能性。
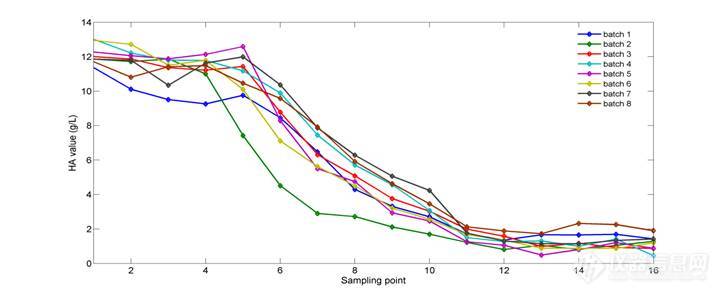
图2 酸沉过程HA含量变化趋势图
3.3 近红外模型的建立
为对酸沉过程进行监测,本研究中建立HA含量测定的PLSR定量分析模型。建立的模型可以对HA含量的变化实时监测,从而实现过程的有效监测和参数的实时调整。
3.3.1 样品集的划分
在模型的建立前需要对样品进行划分,从8批样品中选取5批样品作为校正集建立模型,选取3批样品作为验证集对模型进行验证。样品集的选择原则为HA含量的最大值和最小值批次作为校正集,剩余的6批样品进行随机的划分。表1为样品集划分信息表,校正集和验证集HA含量的平均值和SD值差别较小,样品集的划分符合要求。
表 1 样品集划分信息表
| 样品集 | 样品数 | 最大值(g/L) | 最小值(g/L) | 平均值(g/L) | SD(g/L) |
| 校正集 | 80 | 13.00 | 0.46 | 5.56 | 4.34 |
| 验证集 | 48 | 12.59 | 0.49 | 5.88 | 4.61 |
3.3.2 缩小浓度区间策略的应用
本研究中HA含量测定模型建立的目的在于监测酸沉过程中HA含量的变化,从而可以实时调整醋酸缓冲液的加入速率,实现过程的经济化和最优化。由图2可知,酸沉过程中HA的含量变化主要集中在前11个取样点,11个点后HA的含量变化不再明显。因此引入缩小浓度区间的策略,即将HA含量变化不明显且对模型应用作用较小的样品点去掉,保留含量变化趋势大的样品建立模型,从而提高模型的准确性和有效性。图3为光谱未经任何处理时采用全部样品点建模和去掉含量变化不明显的样品点建模得到的模型结果,表2列出了HA含量全样品建模和局部样品建模得到的各参数的结果比较,通过对Rc2、Rp2、RMSECV、RMSEP等参数的比较,结果显示采用缩小浓度区间的策略可以大大提高模型的准确性,从而更准确的进行酸沉过程HA含量的定量监测。
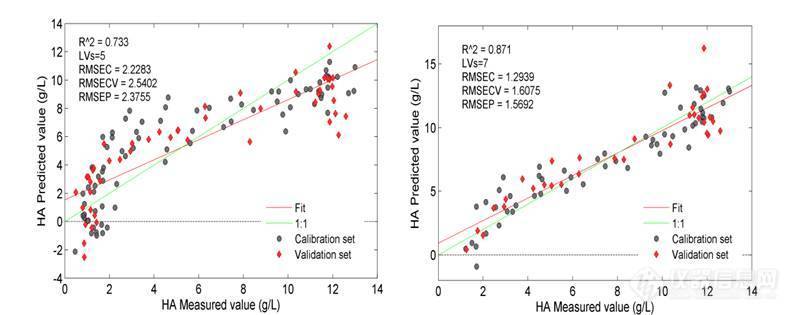
图3 无处理HA测定建模结果(a: 全部样品结果 b: 每个批次前11个样品结果)
表2 全样品和局部样品建模结果比较
| 建模样品 | Rc2 | Rp2 | RMSECV (g/L) | RMSEP (g/L) |
| 全样品 | 0.733 | 0.740 | 2.5402 | 2.3755 |
| 局部样品 | 0.890 | 0.838 | 1.6075 | 1.5692 |
3.3.3 光谱的预处理
本研究中以导数加SG平滑和mean center方法对光谱预处理。在对光谱进行导数加SG平滑的处理时两个主要的参数是导数的阶次和平滑窗口的宽度。由于在高阶次的求导过程中噪声会被不断的放大,因此过高的导数阶次可能无法提高光谱的质量。此外,在平滑过程中,过窄的平滑窗口宽度起不到消除噪声的作用,过宽的平滑窗口又会丢失大量的光谱信息。因此寻找合适的导数阶次和平滑点数对光谱的质量至关重要,本研究中对导数的阶次和最佳的平滑窗口宽度进行了考察。
表3为不同的导数阶次处理后得到的模型结果,以RMSECV和RMSEP值作为模型的评价标准,导数的同时采用软件默认的窗口宽度15点进行SG平滑,结果显示一阶导数对光谱进行预处理得到较好的模型结果。图4为对光谱进行一阶导数(图a)和四阶导数(图b)处理后得到的谱图,从图中可以看出经四阶导数处理后噪声明显比一阶导数处理后的光谱大很多,严重掩盖了有效的光谱信息,降低了光谱的质量。
表3 不同导数阶次建模结果
| 评价参数 | 导数阶次 |
| 一阶 | 二阶 | 三阶 | 四阶 |
| RMSECV (g/L) | 1.5499 | 2.0681 | 2.4368 | 2.8999 |
| RMSEP (g/L) | 1.4262 | 1.6234 | 2.5319 | 2.9745 |
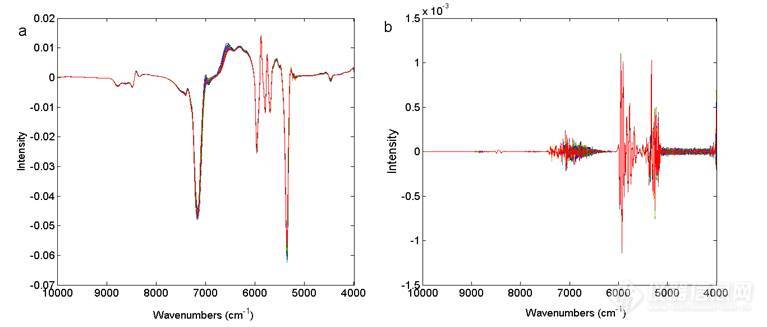
图4 一阶导数和四阶导数光谱对比图 (a: 一阶导数处理光谱图 b: 四阶导数处理光谱图)
图5为平滑窗口宽度的考察结果,以RMSECV和RMSEP值作为评价指标对结果进行评价,结果显示不同的平滑窗口宽度对模型有较大的影响。随着平滑点数的不断增加RMSECV值不断的下降,而RMSEP值在平滑点数为21时出现的最小值,随后不断的升高。由于过宽的平滑窗口宽度会致使一些有效信息的丢失,因此选择21点作为最佳的平滑窗口宽度。
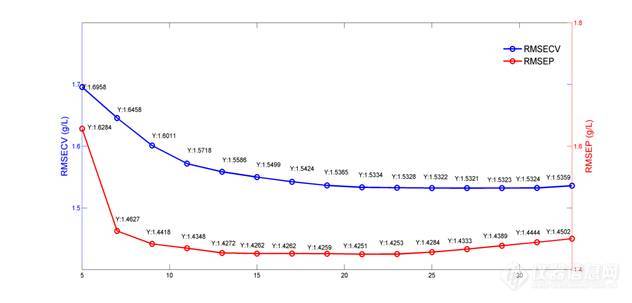
图5平滑中不同窗口宽度考察结果
图6为经过一阶导数+SG21点平滑后得到的HA含量测定的建模结果,通过和未经预处理的模型的RMSECV和RMSEP值(见图3 b)比较,结果显示经过对光谱的处理后,光谱的质量得到了提高,模型的结果变得更优。
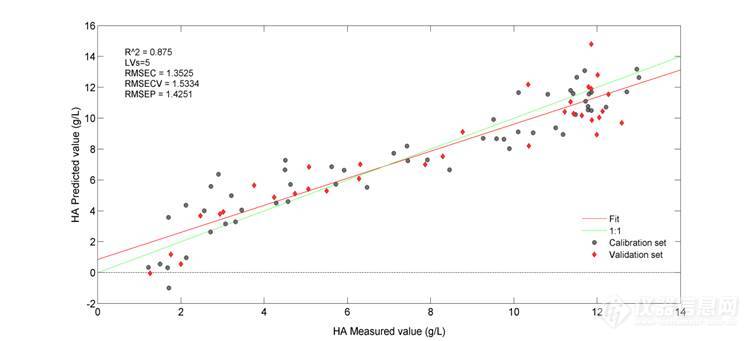
图6 一阶导数+SG21点平滑预处理后建模结果
3.3.4 建模变量的选择
为有效消除无关信息对模型的影响,提高定量分析模型的准确度,本研究中采用多种变量选择方法选出建模变量建立PLSR模型,以RMSECV和RMSEP值的和作为模型的评价标准,其值越小说明模型越好。通过对比选择最佳的参与建模的变量,从而实现模型的最优化和最简化。
3.3.4.1 CC法
将预处理后的校正集光谱与HA的含量值进行相关性分析,相关系数绝对值 (|R|)大的变量可能代表更多的有效信息,得到的建模结果更好。表4为得到的主要建模参数对比结果。由表中显示不同|R|下选择的变量建模较全光谱建模结果更优,表明CC法可以有效去除无用信息,提高建模结果。由RMSECV+RMSEP值可知当|R|为0.60时,即选择|R|大于0.60的变量建模时得到最佳的模型结果。这是因为|R|较小时,此时选择的变量包含有无关信息变量,对模型造成干扰;|R|较大时选择的变量较少,可能去除了一些有用信息,从而导致模型的有效性降低。因此CC法中|R|值的选择至关重要,决定了模型的优劣,需要科学的分析以选择最佳的|R|值,得到最佳的建模变量和最优的定量分析模型。
图7为CC法变量选择和建模结果图,选择的变量集中在6100-5700 cm-1和8500-8300 cm-1这两个波段,主要是C-H的一级倍频和二级倍频吸收,而C-H基团广泛存在于蛋白质分子中。最终得到的RMSECV+RMSEP值为1.3423 g/L,
表4 CC法建模参数比较
| 评价参数 | 相关系数绝对值 |R| |
| 全 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 |
| RMSECV (g/L) | 1.5334 | 0.7872 | 0.7821 | 0.7815 | 0.7765 | 0.7287 | 0.7226 | 0.7141 | 0.9250 | 1.0889 | 1.3281 |
| RMSEP (g/L) | 1.4251 | 0.9860 | 0.6337 | 0.6335 | 0.6303 | 0.6339 | 0.6320 | 0.6282 | 0.7191 | 0.9701 | 1.2708 |
| RMSECV+RMSEP (g/L) | 2.9585 | 1.7731 | 1.4158 | 1.4150 | 1.4069 | 1.3626 | 1.3547 | 1.3423 | 1.6441 | 2.0589 | 2.5990 |
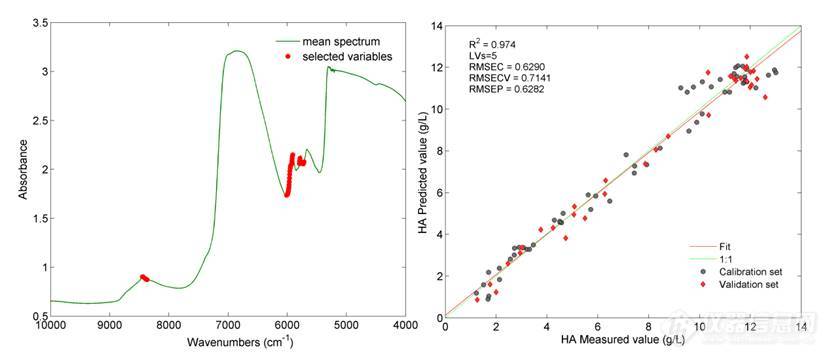
图7 CC法最佳变量选择及建模结果
3.3.4.2 SPA法
SPA是常用的建模变量选择方法。本研究中经过SPA法变量筛选后,建模变量由1557个减少到4个,分别为波数7173.9 cm-1、7100.6 cm-1、5959.0 cm-1和5773.8 cm-1,主要为C-H的一级倍频及组合频的吸收波段。表5为SPA法选择的4个变量建模与全光谱建模得到的对比结果,显示经SPA法选择后,参与建模的变量数大大减少,模型的有效性提高。图8为SPA法变量选择结果及建模结果图,4个变量建模得到的RMSECV+RMSEP值为1.7559 g/L。
表5 SPA法选择变量建模与全光谱建模结果对比
| 建模变量 | 变量数 | RMSECV (g/L) | RMSEP (g/L) | RMSECV+RMSEP (g/L ) |
| 全波段 | 1557 | 1.5334 | 1.4251 | 2.9585 |
| SPA选择变量 | 4 | 0.9966 | 0.7593 | 1.7559 |
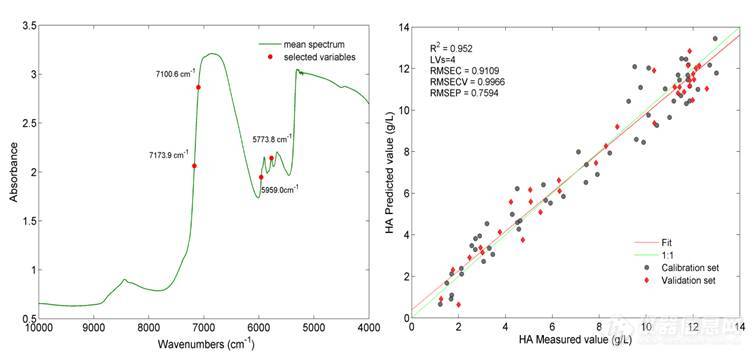
图8 SPA法变量选择及模型结果
3.3.4.3 UVE法
UVE法是根据噪声中回归系数平均值和标准偏差的商的绝对值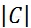 选择变量的方法。本研究中首先对噪声比例进行了考察,以噪声比例为0.9、噪声变量为1000为例,方法为将UVE法得到的噪声的
选择变量的方法。本研究中首先对噪声比例进行了考察,以噪声比例为0.9、噪声变量为1000为例,方法为将UVE法得到的噪声的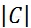 升序排列,选择光谱变量中
升序排列,选择光谱变量中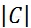 值高于第900个噪声的
值高于第900个噪声的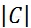 值的变量作为建模变量。由表6可知,当噪声比例为0.99时模型得到最佳的结果,原因可能是噪声比例较高时,可能会去掉一些
值的变量作为建模变量。由表6可知,当噪声比例为0.99时模型得到最佳的结果,原因可能是噪声比例较高时,可能会去掉一些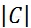 值较小的有用信息变量;噪声比例较低时,选择的变量中可能包含一些
值较小的有用信息变量;噪声比例较低时,选择的变量中可能包含一些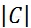 值较高的无关信息变量。
值较高的无关信息变量。
表6 噪声比例考察结果
| 评价参数 | 噪声比例 | |
| 全光谱 | 0.8 | 0.85 | 0.9 | 0.95 | 0.99 | 1 |
| RMSECV (g/L) | 1.5334 | 0.8707 | 0.8347 | 0.7753 | 0.9089 | 0.7218 | 0.7752 |
| RMSEP (g/L) | 1.4251 | 1.4009 | 1.3264 | 1.3062 | 1.1214 | 0.6771 | 0.6675 |
| RMSECV+RMSEP (g/L) | 2.9585 | 2.2716 | 2.1611 | 2.0815 | 2.0302 | 1.3990 | 1.4427 |
| | | | | | | | | |
由于UVE法根据随机产生的噪声选择变量,每次程序运行时随机产生的噪声不同选择参与建模的变量也会不同,得到的模型结果也有一定的差异。因此本研究考察了与光谱变量数相同的随机噪声数(即1557个随机噪声变量)以及光谱变量数两倍的随机噪声数(即3114个随机噪声变量)对模型的影响,同时每个条件下随机运行10次选择参与建模的变量,分析结果见表7所示。以RMSECV+RMSEP的值作为模型的评价指标,结果显示对于两个考察条件,10次变量选择得到的建模结果均有一定的差异,因此采用UVE法进行变量选择时需要对随机噪声数进行深入的考察,同时重复多次进行选择,以得到更加理想的模型结果。同时分析了10次模型结果的标准偏差,由表7中可知当随机噪声数为3114时得到的模型参数的波动性稍小于随机噪声数为1557时得到的建模结果的波动性,原因可能为当产生的随机噪声的数量越多时,多次运行得到的结果间的差异就会越小,得到的建模结果可能越接近。
表7 随机噪声变量数考察结果
| 随机噪声数 | 评价参数 | 随机运行数 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | SD |
| 1557 | RMSECV (g/L) | 0.7218 | 0.7530 | 0.7317 | 0.7206 | 0.7321 | 0.7414 | 0.7246 | 0.7192 | 0.7503 | 0.7485 | 0.0131 |
| RMSEP (g/L) | 0.6771 | 0.7118 | 0.6587 | 0.6772 | 0.6592 | 0.7007 | 0.6858 | 0.6796 | 0.7145 | 0.7171 | 0.0218 |
| RMSECV+RMSEP (g/L) | 1.3990 | 1.4648 | 1.3904 | 1.3978 | 1.3913 | 1.4421 | 1.4104 | 1.3988 | 1.4647 | 1.4656 | 0.0328 |
| 建模变量数 | 351 | 375 | 361 | 348 | 357 | 369 | 356 | 315 | 379 | 384 | 19.8 |
| 3114 | RMSECV (g/L) | 0.7485 | 0.7413 | 0.7236 | 0.7232 | 0.7219 | 0.7413 | 0.7219 | 0.7310 | 0.7530 | 0.7399 | 0.0117 |
| RMSEP (g/L) | 0.7171 | 0.6993 | 0.6760 | 0.6766 | 0.6772 | 0.6993 | 0.6774 | 0.6621 | 0.7118 | 0.7003 | 0.0181 |
| RMSECV+RMSEP (g/L) | 1.4656 | 1.4405 | 1.3996 | 1.3997 | 1.3991 | 1.4405 | 1.3993 | 1.3931 | 1.4648 | 1.4402 | 0.0290 |
| 建模变量数 | 384 | 366 | 340 | 344 | 350 | 366 | 352 | 364 | 375 | 368 | 14.0 |
由表7中可知随机噪声数为1557时第3次运行得到了最佳的模型结果,此时参与建模的变量为361个,图9为最佳模型变量选择结果,选择的变量所在的光谱区间主要集中在4700-4500 cm-1、6500-5300 cm-1、9000-7200 cm-1三个波段范围。图1-10为UVE法选变量得到的最佳模型结果,最终得到的RMSECV+RMSEP值为1.3904 g/L。
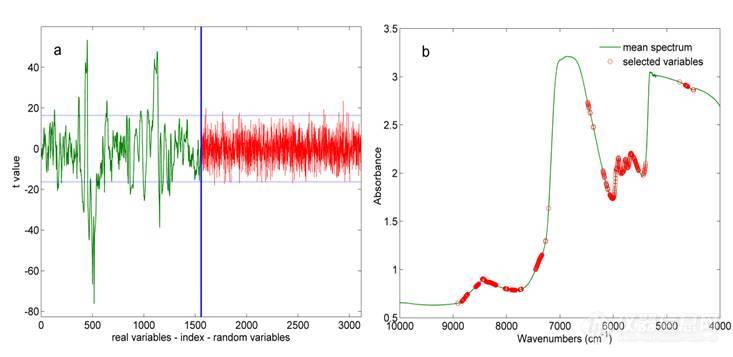
图9 UVE法变量选择结果
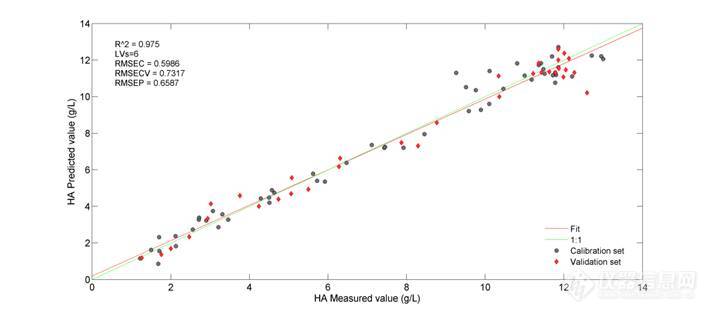
图10 UVE法变量选择最佳建模结果
3.3.4.4 CARS法
以CARS法进行变量选择时蒙特卡洛采样次数以及LVs的选择对模型结果影响较大,因此对这两个参数进行了考察。图11为考察结果图,由图中可知不同蒙特卡洛采样次数和LVs下选择的变量建模得到的结果均有一定的差异。当LVs高于7时,随着LVs的增加RMSECV+RNSEP值不断变大,说明模型的有效性不断下降。当蒙特卡洛采样次数为50,LVs为7时得到最佳的分析模型,此时参与建模的变量为7个,且7个变量集中在6100-5600 cm-1区间。图12为CARS法选择得到的参与建模的变量及最终得到的模型结果图,最优模型的RMSECV+RMSEP值的为1.4183 g/L。
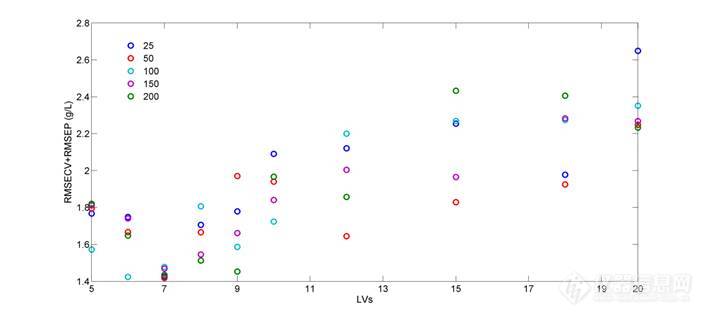
图11 CARS法最优参数考察
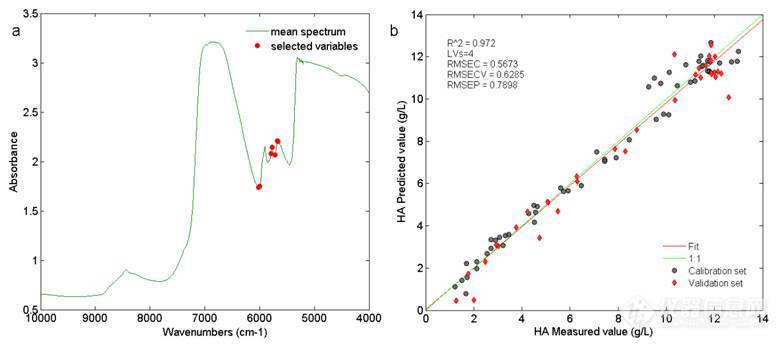
图12 变量选择及建模结果
3.3.4.5 SCARS法
SCARS算法是由CARS法演变而来的变量选择方法。在采用本方法进行变量选择时同样考察了蒙特卡洛采样次数和LVs对结果的影响以寻求最优参数。图13为参数考察结果,可知不同蒙特卡洛采样次数和LVs值下的模型结果不同且不具有规律性,总体上看当LVs值较大时得到的模型结果不理想。当蒙特卡洛采样次数为100,LVs为6时得到了最佳的分析模型,图14为SCARS法选择得到的最佳建模变量及最优模型结果,此时11个变量参与建模,主要集中在波段6100-5600 cm-1之间,得到模型的RMSECV+RMSEP值为1.3906 g/L。
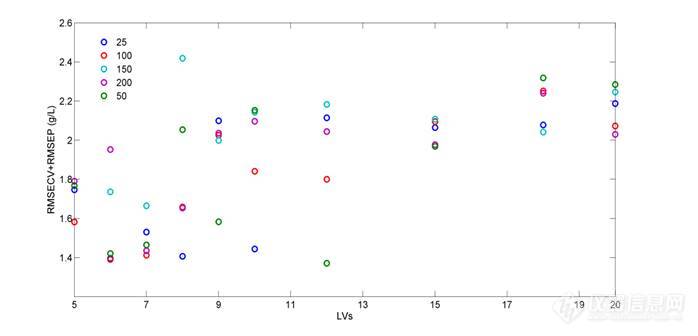
图13 SCARS法最优参数考察
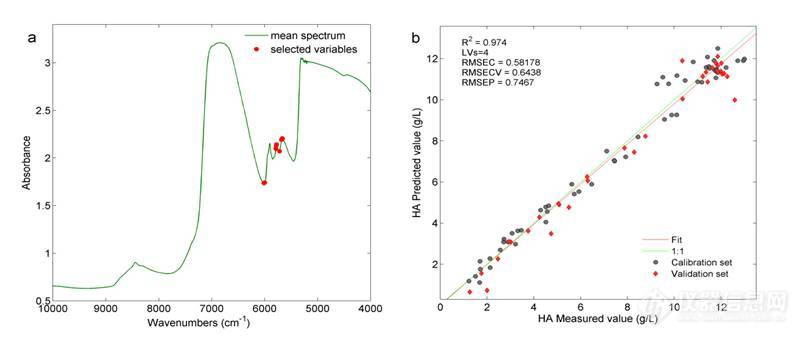
图14 SCARS法变量选择(a)及建模结果(b)
3.3.4.6 FiPLS法
FiPLS法选择变量时变量窗口宽度的大小对结果将产生较大的影响,如果宽度太小将大大增加计算量,宽度太大则有可能增加选择无用信息变量的机会。本研究中考察了50至400之间的8个窗口宽度值,表8为得到的窗口宽度考察结果,当每个宽度为100个变量时得到了最佳的模型结果。图15 a为变量选择结果图,此时选择的用于建模的变量区间为5924-5542 cm-1、8238-7857 cm-1和9781-9399 cm-1,主要反映了S-H的一级倍频吸收、C-H的二级倍频吸收以及O-H的二级倍频吸收。图15 b为FiPLS法最佳模型结果图,得到的RMSECV+RMSEP值为1.4395 g/L。
表8 FiPLS法窗口宽度考察结果
| 评价参数 | 窗口宽度 | |
| 全 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| RMSECV (g/L) | 1.5334 | 0.7258 | 0.7324 | 0.6768 | 0.8519 | 0.7316 | 0.7777 | 0.6807 | 0.7916 |
| RMSEP (g/L) | 1.4251 | 0.7273 | 0.7071 | 0.9978 | 0.8181 | 0.8269 | 0.8638 | 1.1031 | 1.3098 |
| RMSECV+ RMSEP (g/L) | 2.9585 | 1.4531 | 1.4395 | 1.6746 | 1.6700 | 1.5585 | 1.6415 | 1.7838 | 2.1014 |
| 建模变量数 | 1557 | 450 | 300 | 450 | 800 | 500 | 600 | 350 | 400 |
| | | | | | | | | | | |
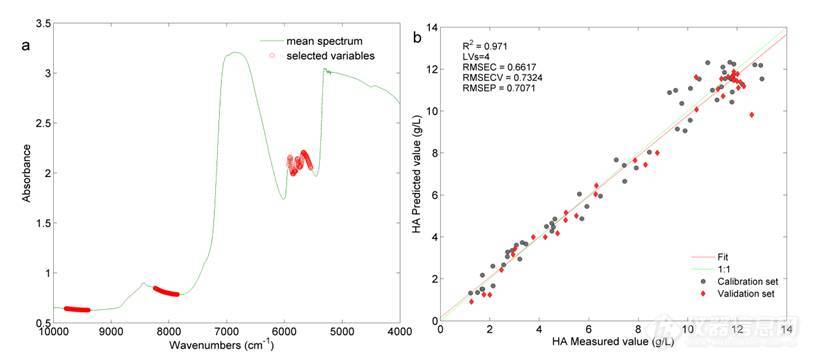
图15 FiPLS法变量选择(a)及建模结果(b)
3.3.4.7 MWPLS法
在用MWPLS法选择变量时窗口的宽度对结果影响较大,本研究中对不同的窗口宽度进行了考察,选择RMSECV值小于0.75 g/L的变量建立模型。表9为窗口宽度考察结果,可见MWPLS法选择变量后的建模结果均优于全光谱建模,随着窗口宽度的增加选择的变量数是先递增后递减的变化规律。以RMSECV+RMSEP值作为模型评价指标,当窗口宽度为151时得到最佳的模型结果。图16 a为选择的建模变量,图中蓝色线代表全波段范围的RMSECV值,红色的水平线为RMSECV为0.75 g/L的阈值线,选择小于0.75的变量建模,黑色线为平均光谱,红色的圆圈为选择的建模变量。此时选择的建模区间为6100-5500 cm-1和8800-7500 cm-1,主要反映了C-H的一级倍频、二级倍频以及组合频的特征吸收。图16 b为建模结果,此时得到的RMSECV+RMSEP值为1.3533 g/L。
表9 MWPLS法窗口宽度考察结果
| 评价参数 | 窗口宽度 | |
| 全 | 21 | 51 | 101 | 151 | 201 | 251 | 301 | 401 |
| RMSECV (g/L) |
1.5334 | 1.1383 | 0.7153 | 0.6548 | 0.6597 | 0.7125 | 0.7003 | 0.6908 | 0.6943 |
| RMSEP (g/L) | 1.4251 | 1.1755 | 0.7072 | 0.7131 | 0.6936 | 0.6726 | 0.7047 | 0.7522 | 0.7621 |
| RMSECV+RMSEP (g/L) | 2.9585 | 2.3138 | 1.4225 | 1.3679 | 1.3533 | 1.3851 | 1.4050 | 1.4430 | 1.4564 |
| 建模变量数 | 1557 | 9 | 40 | 352 | 459 | 520 | 651 | 627 | 593 |
| | | | | | | | | | | | |
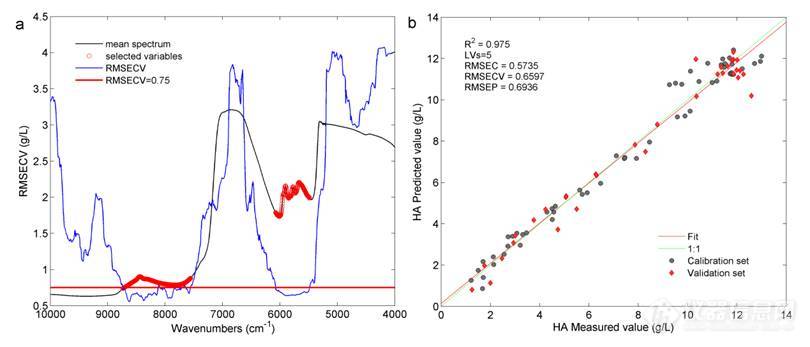
图16 MWPLS法变量选择(a)及建模结果(b)
3.3.4.8 BiPLS法
和其它iPLS法类似,窗口宽度(或区间数)对最终的结果将会产生较大的影响,因此本研究中对区间数进行了分析考察,结果见表10所示。以RMSECV+RMSEP值作为考察指标,当区间数为8时得到最佳的模型结果。图17 a为选择得到的建模变量,变量所在的光谱区间为8505-7760 cm-1和10000-9257 cm-1,主要反映了C-H的二级倍频及组合频的吸收和O-H的二级倍频吸收。图17 b为最佳模型结果,此时得到的RMSECV+RMSEP值为1.4637 g/L。
表10 BiPLS法区间数考察结果
| 评价参数 | 区间数 |
| 全 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 18 | 20 | |
| RMSECV (g/L) | 1.5334 | 0.7230 | 0.7518 | 0.6879 | 0.6949 | 0.6880 | 0.8215 | 0.6585 | 0.6597 | 0.6071 | 0.7504 | |
| RMSEP (g/L) | 1.4251 | 0.8562 | 0.8871 | 1.0278 | 0.7688 | 0.7801 | 0.7641 | 1.0676 | 1.1246 | 1.2782 | 0.9825 | |
| RMSECV+RMSEP (g/L) | 2.9585 | 1.5792 | 1.6389 | 1.7157 | 1.4637 | 1.4681 | 1.5856 | 1.7261 | 1.7843 | 1.8853 | 1.7329 | |
| 建模变量数 | 1557 | 622 | 518 | 444 | 388 | 346 | 622 | 259 | 829 | 605 | 777 | |
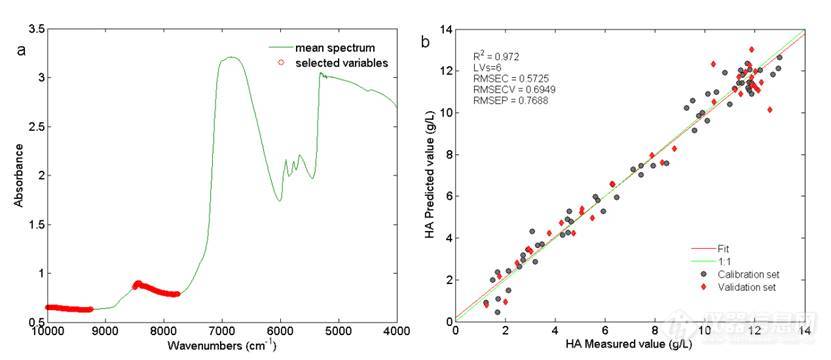
图17 BiPLS法变量选择(a)及建模结果(b)
3.3.4.9 与SPA联用变量选择
本研究中SPA变量选择方法可以有效的去除光谱变量的共线性问题,而其它方法则选择有效信息变量。实际上,选择的有效信息变量中常存在变量的共线性问题,增加了模型的复杂程度。因此,通过常用的变量选择方法选择有效信息变量,然后再利用SPA法去除所选变量的共线性将大大的简化模型。本研究中将不同的变量选择方法和SPA方法联合应用,以考察变量选择的有效性。首先,用CC、UVE、CARS、SCARS、FiPLS、MWPLS、BiPLS法等选择变量,然后通过SPA法对得到的有用信息变量进行进一步选择,以去除共线性变量,从而有效的简化模型。表11为不同变量选择方法与SPA法联用得到的模型结果,结果显示除了BiPLS-SPA法选择了17个变量外,其余方法参与建模的变量数均不高于5个,CARS-SPA和SCARS-SPA均选择了5774 cm-1和5670 cm-1两个变量点建模,这可能与这两种方法选择变量的原理相似有关系。以RMSECV+RMSEP值为模型评价指标,联用后得到的模型结果均优于仅采用SPA法得到的模型结果。BiPLS-SPA法选择变量建模得到的RMSECV+RMSEP值为1.2921 g/L,小于其它变量选择方法得到的结果,但是RMSEP(0.8455 g/L)和RMSEC(0.3221 g/L)的比值为2.62(远远大于1.2),说明模型存在过拟合现象,最终选择CC-SPA法为最佳的联用变量选择方法。
图18为不同算法与SPA联用得到的变量选择结果图,图中显示选择的建模变量主要集中在6000-5350 cm-1这一光谱区间,反映了C-H的一级倍频吸收峰,此外UVE-SPA和MWPLS-SPA法分别选择了波数为7212cm-1和7594 cm-1的变量,反映了C-H的组合频吸收峰。而BiPLS-SPA法选择的变量区间集中在8500-8000 cm-1和10000-9500 cm-1这两个光谱区间,反映了C-H的二级倍频吸收和O-H的二级倍频吸收。本研究中测定的目标物质是HA,C-H基团广泛存在于蛋白质分子中,因此选择的变量恰好为目标物质的基团吸收。
经过与SPA法联用后选择参与建模的变量数目大大减少,得到的模型RMSECV+RMSEP值有的优于单独一种方法选择变量得到的结果,有的则不如单独一种方法选择变量得到的结果,说明和SPA法联用后可能会进一步选择更有价值的信息变量,可能会丢失部分有价值的信息变量,在模型的建立中需要充分的考察和分析,以得到最佳的模型结果。
表11 与SPA法联用选变量建模结果
| 评价参数 | 变量选择方法 | |
| SPA | CC-SPA | UVE-SPA | CARS-SPA | SCARS-SPA | FiPLS-SPA | MWPLS-SPA | BiPLS-SPA |
| RMSECV (g/L) | 0.9966 | 0.7085 | 0.9218 | 0.7310 | 0.7310 | 0.7277 | 0.7789 | 0.4466 |
| RMSEP (g/L) | 0.7593 | 0.6267 | 0.6037 | 0.8160 | 0.8160 | 0.6622 | 0.5871 | 0.8455 |
| RMSECV+RMSEP (g/L) | 1.7559 | 1.3352 | 1.5255 | 1.5470 | 1.5470 | 1.3899 | 1.3660 | 1.2921 |
| 建模变量数 | 4 | 4 | 4 | 2 | 2 | 3 | 5 | 17 |
| | | | | | | | | | | |
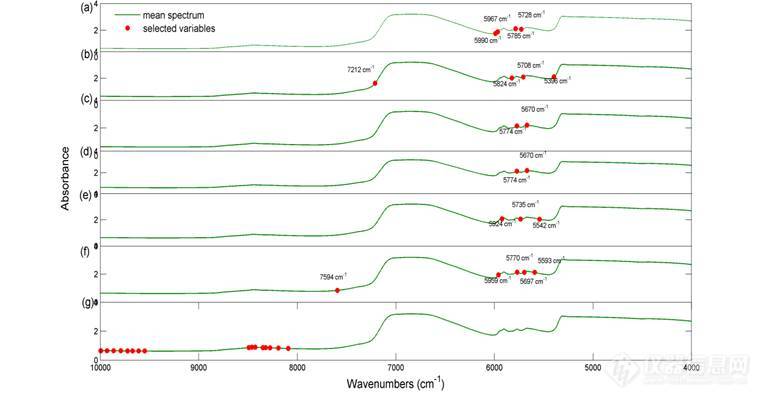
图18 与SPA联用变量选择结果
(a: CC-SPA b:UVE-SPA c: CARS-SPA d: SCARS-SPA e: FiPLS-SPA
f: MWPLS-SPA g: BiPLS-SPA)
3.3.4.10 基于与SPA联用的变量选择
为进一步寻找最佳的变量建立用于HA测定的定量分析模型,本研究中对不同变量选择方法和SPA法联用选择的总共35个变量(图18中所示35个变量)结合起来建立模型。表12为得到的建模结果,显示将不同方法与SPA联用后选择的35个变量组合在一起建模,RMSECV+RMSEP值小于各方法单独与SPA联用的结果,模型的有效性提高。其主要原因可能是将不同的变量组合在一起克服了不同变量选择方法的弊端,选择的变量包含了大部分的有效光谱信息。图20为参与建模的35个变量和建模结果图,其中参与建模的变量信息在3.3.4.9中已经进行了讨论,最终35个变量建模得到的RMSECV+ RMSEP值为1.2931 g/L。
表12 不同方法与SPA法联用选择变量考察
| 变量选择方法 | 变量数 | RMSECV (g/L) | RMSEP (g/L) | RMSECV+RMSEP (g/L ) |
| 基于SPA联用 | 35 | 0.7038 | 0.5893 | 1.2931 |
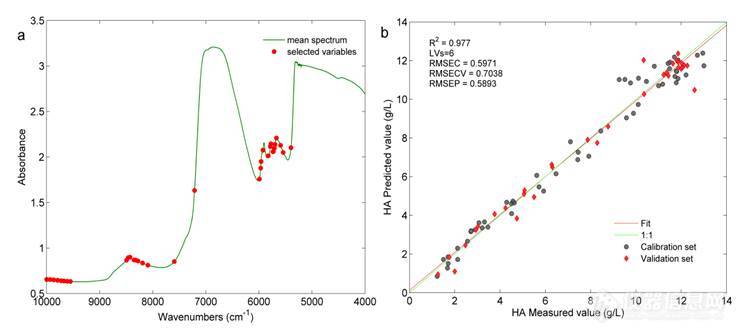
图20 变量组合及建模结果
3.3.4.11 不同变量选择方法比较
由上面不同变量选择方法选择变量得到的结果显示不同的方法选择的用于建模的变量数和变量所在的光谱区间存在较大的差异,表13为不同方法选择的变量得到的建模结果。与全波段建模结果相比,经过不同方法的变量选择后模型的预测能力均大大提高,参与建模的变量大大降低。其中不同的变量选择方法与SPA联用后得到的变量总和(35个变量)建模得到了最佳的模型结果,模型的Rc2、Rp2、 RMSEC、RMSECV、RMSEP分别为0.977、0.978、0.5971 g/L、0.7038 g/L、0.5893 g/L,该模型作为酸沉过程HA含量测定的最优近红外模型。
表13 不同变量选择方法建模结果对比
| 方法 | Rc2 | Rp2 | RMSEC (g/L) | RMSECV (g/L) | RMSEP (g/L) | RMSECV+RMSEP (g/L) | LVs | 变量数 |
| 无 | 0.879 | 0.869 | 1.3525 | 1.5334 | 1.4251 | 2.9585 | 5 | 1557 |
| CC | 0.974 | 0.976 | 0.6290 | 0.7141 | 0.6282 | 1.3423 | 5 | 52 |
| SPA | 0.945 | 0.962 | 0.9109 | 0.9966 | 0.7593 | 1.7559 | 4 | 4 |
| UVE | 0.976 | 0.973 | 0.5986 | 0.7317 | 0.6587 | 1.3903 | 6 | 361 |
| CARS | 0.979 | 0.965 | 0.5673 | 0.6285 | 0.7898 | 1.4183 | 4 | 7 |
| SCARS | 0.978 | 0.972 | 0.5818 | 0.6438 | 0.7467 | 1.3906 | 4 | 11 |
| FiPLS | 0.971 | 0.974 | 0.6617 | 0.7324 | 0.7071 | 1.4395 | 4 | 300 |
| MWPLS | 0.978 | 0.970 | 0.5735 | 0.6597 | 0.6936 | 1.3533 | 5 | 459 |
| BiPLS | 0.978 | 0.961 | 0.5725 | 0.6949 | 0.7688 | 1.4637 | 6 | 388 |
| CC-SPA | 0.972 | 0.978 | 0.6471 | 0.7085 | 0.6267 | 1.3352 | 4 | 4 |
| 基于与SPA联用 | 0.977 | 0.978 | 0.5971 | 0.7038 | 0.5893 | 1.2931 | 6 | 35 |
3.4 模型的评价
图21为3个验证集批次的样品参考值和预测值的对比图,由图中显示酸沉过程HA含量参考值的变化趋势和NIRS的预测值大致相同,但是有个别样品参考值和预测值间有较大的差别,其可能的原因包括模型的预测精度不够、参考方法测定的结果有偏差等。
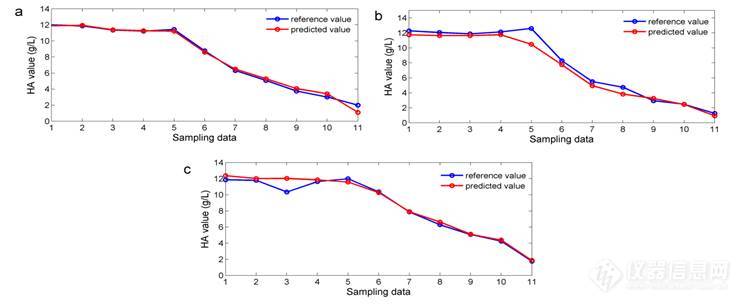
图21 验证集预测值与参考值对比图(a: batch 6 b: batch 7 c: batch 8)
为进一步考察模型的预测能力,利用配对t检验分别对验证集样品进行统计学分析。由表14配对t检验统计结果可知,NIRS法与传统的BCG法得到的结果的均值和SD值非常接近,在95%的置信限下得到的P=0.374>0.05,说明两种方法测定结果之间不存在显著性差异,说明NIRS法可替代传统方法进行HA含量的快速测定。
表14 验证集样品配对t检验统计结果
| 方法 | 样品量 | 平均值(g/L) | SD(g/L) | t检验(0.05) |
| t | P |
| NIRS | 33 | 8.06 | 3.9 | 0.902 | 0.374 |
| BCG | 33 | 7.97 | 3.9 |
4讨论和结论
本研究中基于缩小浓度区间策略和多种变量筛选方法,建立了FIV上清酸沉过程HA含量测定的定量分析模型,以实现酸沉过程中HA含量的测定。首先,实验室条件下模拟8批酸沉过程并在过程中进行取样,用传统的BCG法测定HA的含量,并采集原始近红外光谱。然后,以缩小浓度区间的策略将HA含量较低且变化不明显的样品点去除,在保证模型有效用于酸沉过程监测的基础上提高模型的预测能力。随后,经过光谱预处理和建模变量选择后建立得到最佳的用于酸沉过程HA含量测定的PLSR定量分析模型。最终用35个变量建立得到了用于HA含量测定的模型,Rc2、Rp2、RMSECV和RMSEP分别为0.977、0.978、0.7038 g/L和0.5893 g/L。配对t检验的结果显示,建立的模型可以实现酸沉过程HA的含量测定,对NIRS用于酸沉环节的过程监测和醋酸缓冲液滴加速率的调整有着重要的借鉴价值。
在模型的建立中采用多种变量选择方法选择建模变量,并且对不同变量筛选方法与SPA的联用进行分析,结果显示将不同变量选择方法与SPA联用选择的变量组合在一起得到的模型结果优于其它的模型结果,分析原因可能是这种方法集合了多种变量选择方法的优点,因此建立得到了最佳的模型。因此,在近红外模型的建立中为了提高模型的有效性,建立得到最佳的用于定量分析的模型,需要对建模变量进行详细的筛选。
同时,由于本研究基于实验室规模开展,和实际的产业化生产模式有一定的差别。但本研究成果作为一种理论指导和可行性分析,为酸沉过程HA含量在线监测和过程控制提供了解决问题的方向,为在线研究提供了扎实的基础。
参考文献
倪道明. 血液制品 (第三版) . 北京: 人民卫生出版社, 2013.
刘欣晏. 人血白蛋白连续流压滤工艺研究. 山东大学, 2008.
KistlerP, Nitschmann H. Large scale production of human plasma fractions. Eight yearsexperience with the alcohol fractionation procedure of Nitschmann, Kistler andLergier . Vox Sang, 1962, 7: 414-424.
杨海龙, 臧恒昌, 胡甜, 等. 近红外漫反射光谱法对不同产地山楂的定性鉴别和定量分析. 药物分析杂志, 2014, 34(3): 396-401.
Li L, Ding B, Yang Q, et al. The relevance study of effectiveinformation between near infrared spectroscopy and chondroitin sulfate in ethanolprecipitation process . J InnovOpt Heal Sci, 2014, 07(06): 1450022.
Wang P, Zhang H, Yang H, et al. Rapid determination of majorbioactive isoflavonoid compounds during the extraction process of kudzu(Pueraria lobata) by near-infrared transmission spectroscopy . Spectrochim Acta A Mol BiomolSpectrosc, 2015, 137: 1403-1408.
Zhang XB, Feng YC, Hu CQ. Feasibility andextension of universal quantitative models for moisture content determinationin beta-lactam powder injections by near-infrared spectroscopy . Anal Chim Acta, 2008, 630(2): 131-140.










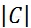 选择变量的方法。本研究中首先对噪声比例进行了考察,以噪声比例为0.9、噪声变量为1000为例,方法为将UVE法得到的噪声的
选择变量的方法。本研究中首先对噪声比例进行了考察,以噪声比例为0.9、噪声变量为1000为例,方法为将UVE法得到的噪声的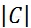 升序排列,选择光谱变量中
升序排列,选择光谱变量中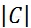 值高于第900个噪声的
值高于第900个噪声的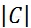 值的变量作为建模变量。由表6可知,当噪声比例为0.99时模型得到最佳的结果,原因可能是噪声比例较高时,可能会去掉一些
值的变量作为建模变量。由表6可知,当噪声比例为0.99时模型得到最佳的结果,原因可能是噪声比例较高时,可能会去掉一些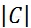 值较小的有用信息变量;噪声比例较低时,选择的变量中可能包含一些
值较小的有用信息变量;噪声比例较低时,选择的变量中可能包含一些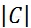 值较高的无关信息变量。
值较高的无关信息变量。










