试用SPSS对COD和BOD进行相关分析

试用SPSS对COD和BOD进行相关分析

依次Analyze分析-Regression回归-Linear线性，出现图1窗口

图1

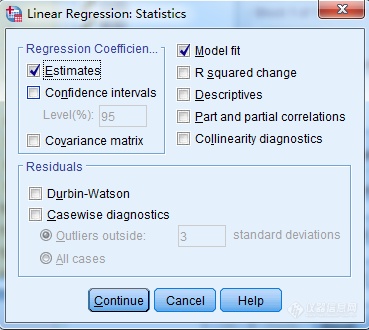
图2

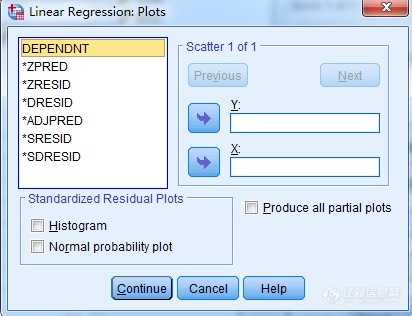
图3

点击save保存，出现图4窗口。此图中Prediction values预测值框中Unstandardized未标准化是回归模型中对因变量BOD的预测值。Standardized标准化是将预测值进行标准化处理即(Y-Y均)/S。Adjusted是当某条自变量记录没参与回归方程系数估计时，所得的回归方程对其对应的预测值。S.E. of Mean predictions是预测值的均值标准误差。

Distances框下各参数意义：Mahalanobis马氏距离：自变量与其均值的距离。此值过大表明自变量取值有异常。Cook库克距离表示把一条记录从计算回归系数的样本中去除时所引起的残差变化大小。此值越大表明此记录回归系数的影响越大。Leverage values杠杆值用以测量单个观测值对拟合效果的影响程度。取值范围是0~n/(n-1)。取0表示此单个观测值对拟合无影响。

Prediction intervals预测区间框用以选择预测值的均值和单个预测值的上下置信限，默认为95%。

Residuals框中Unstandardized未标准化是观测值与预测值之差。Standardized标准化是令残差均值为0，标准差为1。Studentized学生化是用残差除以残差标准差的估计值。Delete删除表示把某条记录从样本中去除时回归所得当前记录的残差，即观测值-调整预测值。学生化删除：用剔除残差除以单个记录的标准误差。学生化与学生化剔除残差间的不同能反映补剔除的观测值在预测自身时的作用大小。

Influence Statistics影响统计框中的各子项是把记录从回归样本中剔除后计算得到的一些统计量。DfBeta剔除某条记录后回归系数的改变（包括常项）。Standardized DfBeta剔除某条记录后回归系数的改变量标准化后的值（包括常项）。当它>2/SQRT(N)时，它对回归系数有较大影响。N为自变量的记录条数。DfFit剔除某条记录后预测值的改变量。Standardized DfFit剔除某条记录后预测值的改变量标准化后的值。当它>2/SQRT(p/N)时，它对回归系数有较大影响。p为模型中的参数个数。

此界面的其它项与一元回归分析无关，就不赘述。

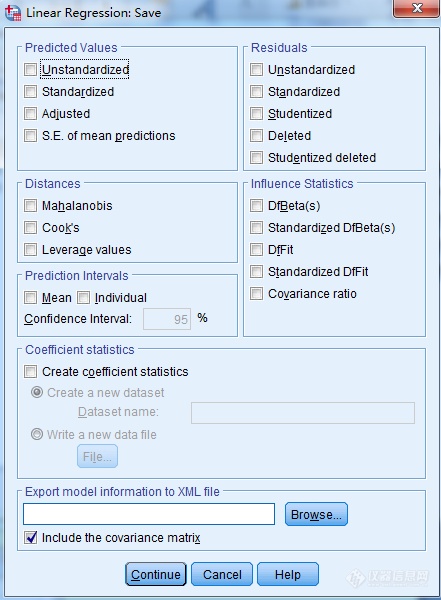
图4

1. 描述性的统计量，包括各变量平均数、标准偏差、有效个案数。

表1

2. 相关性表列出相关系数矩阵及其单侧显著性水平。COD与BOD的相关系数为0.979。显著性为0.000，也说明二者显著相关。

表2

3.模型摘要

表中显示了输入的变量COD，有一个模型，无剔除的变量。表4是模型摘要表，提供了模型拟合情况。表中可看出R2为0.958，调整后为0.956变化极微，说明COD自变量对模型的贡献较大。显著性F的变化量为0.000，说明COD和BOD间存在显著相关。DW值=2.061，接近于2，说明回归分析残差不存在自相关，也就是相互独立的。

表3

表4

4.ANOVA方差分析表解读

观测值COD的总离差平方和为1179.339，其可解释的变差为1130.109，抽样误差引起的变差为49.230。二者方差分别为1130.109和2.735，相除得F统计量的观测值=413.203，对应的概率P值=0小于显著水平α（一般取α=0.05）也表明COD和BOD有显著相关。

表5

5.回归系数的估计值表

根据此表给出的模型建立的回归方程为：BOD=0.561*COD-6.996。在95%的置信概率下斜率的范围在0.503~0.619之间，常数项范围在-10~-3.597之间。

表6

6. 残差分析

残差分析是指由回归方程计算所得的预测值与实际样本值之间的差距。这是回归方程的重要部分。如果回归方程能反映自变量与因变量的特征和变化规律，则残差不应有明显的规律性和趋势性。

从表7 的残差统计表及图5的直方图和图6的正态概率图可看出残差基本上服从正态分布。图7的残差散点图中也可看出回归标准化残差都在±3以内，无异常值，也说明残差是相互独立的。

表7

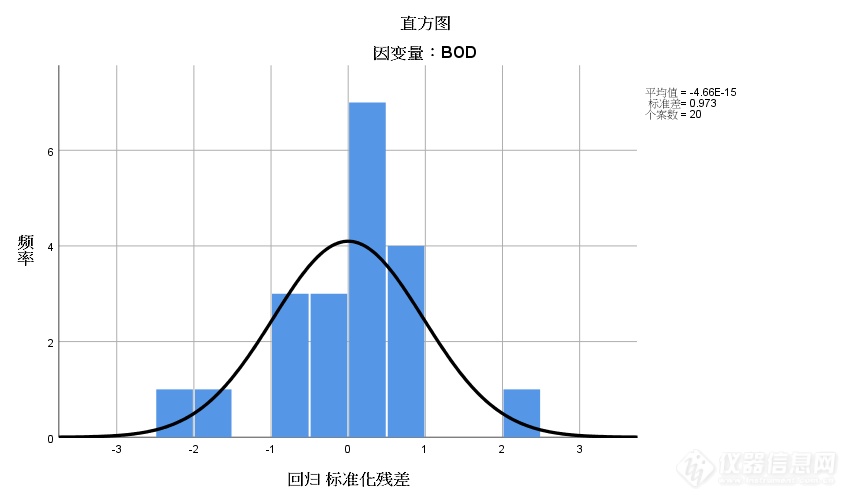
图5

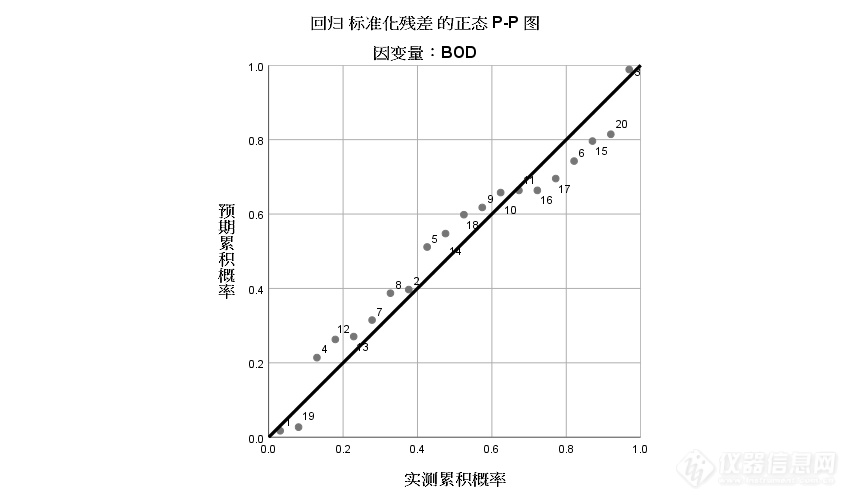
图6

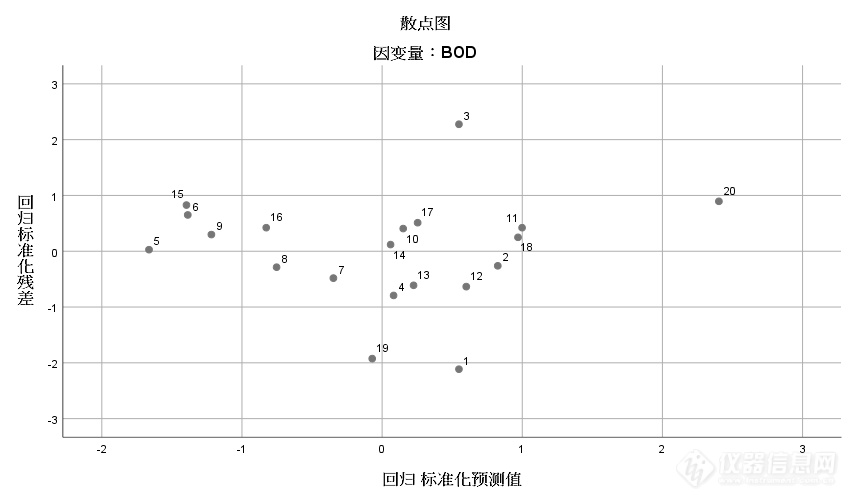
图7