

批次间数据的变异的计算和分析
——对2015年药物稳定性研究指导技术的思考
国家食品药品监督管理总局药品审评中心在2015年2月5日发布了新修订的《化学药物(原料药和制剂)稳定性研究技术指导原则》(以下简称指导原则)。该指导原则与老版本的指导原则相比最大的不同是新版本把原料药和制剂分开规定,增加了影响因素实验条件。在这里我们关注原指导原则的第五部分第三条“有效期的确定”在新的指导原则用“结果的分析评估”(原料药第六部分制剂第七部分来替换和扩充。
1新旧指导原则对结果统计分析的描述
旧的指导原则其中对结果论述“如三批统计分析结果差别较小,则取其平均值为有效期,如差别较大则取其最短的为有效期。若数据表明测定结果变化很小,提示药品是很稳定的,则可以不做统计分析”。新的指导原则论述“如果稳定性数据表明试验制剂的降解与批次间的变异均非常小,从数据上即可明显看出所申请的有效期是合理的,此时通常不必进行正式的统计分析,只需陈述省略统计分析的理由即可。如果稳定性数据显示试验制剂有降解趋势,且批次间有一定的变异,则建议通过统计分析的方法确定其有效期”。用变异很小来代替差别较小的说法,科学而且提供的分析方案。
2 数据变异——从一组数据到多组数据
首先说一下变异。我们最想到的统计量是变异系数(Coefficient of Variation,CV)。变异系数是标准偏差(SD)和平均值(x)的比值(式1),我们可以认为CV与常见的相对标准偏差(RSD,relative standard deviation)一致(有些地方认为两个统计量是有差异的)。在分析方法验证中,我们用RSD评价重复性精密度等指标,这些指标都是一组数据(一位实验人员一个仪器1份或者多份样品重复进样)。一般认为RSD≤5%的一组数据重复性就好,数据间的变异小(数据没啥变化)。在稳定性试验中,样品是多批次的,数据也是多组的,数据量比较大,新的指导原则要求稳定性数据要表明“试验制剂的降解与批次间”变异,其中“试验制剂的降解”通过计算每个批次不同时间段的数据RSD来评价变异,那么“批次间”的变异呢?我们一般会想到的计算方式有两种:1、三个或者多个批次(根据实际申报批次)所有数据合并在一块算RSD;2、每个批次计算平均值,计算平均值的RSD。以上两种计算方法都有不足,方法1首先进行了数据合并,在统计上对数据合并是有要求的,方差和均值相等的数据才能认为来自一个整体,数据可以合并,合并计算的前提就是认为几个批次间的数据变异小。在新的指导原则“结果的分析评估”中规定“如果分析结果表明批次间的变异较小(对每批样品的回归曲线的斜率和截距进行统计检验),即P值>0.25(无显著性差异),最好将数据合并进行整体分析评估。如果批次间的变异较大(P值≤0.25),则不能合并分析,有效期(复检期)应依据其中最短批次的时间确定。”方法2比较平均值,最终用来统计的数据只有3个(一般药物申报3个批次)或者多个,经过加工处理的数据会极大的掩盖数据的真实情况。
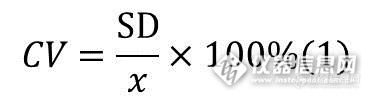
我们在比较不同组数据的变异主要比较的是两个指标:方差和均值,统计上均值比较的常用方法有t检验和单因素方差分析(one-way ANOVA),t检验比较的是两组数据,ANOVA比较的是多组数据(有人会问多组数据也可以两个配对的做t检验,当实验组数比较多的时候,比如6组,就需要比较15次,而且会增加误差),通过这两个检验来判断不同组数据是不是有差异。
3 多组数据分析——一个长期稳定性实验数据分析实例
以一次长期稳定性试验中数据为例(表1),实验周期为1年,2个月检测一次有效成分含量,对其做方差分析,所用软件为SPSS Statistics 19。分析结果如下:
| 检查时间 | 批次1 | 批次2 | 批次3 |
| 0 | 1.99081 | 2.06529 | 1.96563 |
| 2 | 2.10935 | 2.03058 | 1.98812 |
| 4 | 2.00003 | 2.06281 | 2.04345 |
| 6 | 1.98095 | 1.99775 | 1.98246 |
| 8 | 2.15492 | 2.0394 | 2.02218 |
| 10 | 1.99116 | 2.03012 | 1.98128 |
表1长期稳定性数据
结果1,该结果是对数据的统计描述,计算了均值,标准差等统计量。
| 描述 | ||||||
| 含量 | ||||||
|
| N | 均值 | 标准差 | 标准误 | 均值的 95% 置信区间 | |
| 下限 | 上限 | |||||
| 1 | 6 | 2.0378683 | .07467142 | .03048448 | 1.9595054 | 2.1162311 |
| 2 | 6 | 2.0376568 | .02489621 | .01016383 | 2.0115298 | 2.0637837 |
| 3 | 6 | 1.9971866 | .02937080 | .01199058 | 1.9663638 | 2.0280094 |
| 总数 | 18 | 2.0242372 | .04963229 | .01169844 | 1.9995557 | 2.0489188 |
结果2,该结果是ANOVA的分析结果,有三项平方和的计算。计算如下:
ANOVA | |||||
含量 | |||||
|
| 平方和 | df | 均方 | F | 显著性 |
| 组间 | .007 | 2 | .003 | 1.400 | .277 |
| 组内 | .035 | 15 | .002 |
|
|
| 总数 | .042 | 17 |
|
|
|
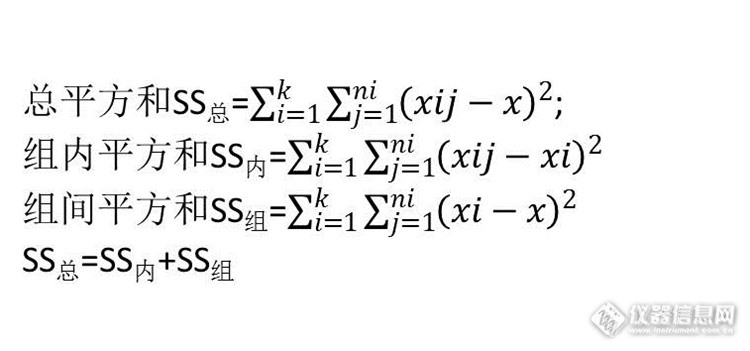
其中k为组数,n为一组数据数,xi为i组均值,x为全部数据均值。
组间平均平方和MS组=SS组/(k-1);
组内平均平方和MS内=SS内/(n-k);
F分布值F=MS组/MS内(看到这里有没有很熟悉,在两组数据里也会用到F检验,一般分析化学书第一章或者第二章会讲到),在F检验表格查某个置信区间的Fk-1,n-k的值,与计算的F值比较,如果F
严格的来说在做ANOVA分析之前要做方差分析,分析数据方差δ2是不是相同,方差不同一般会调整自由度k和n,这个我只会使用但是不理解,这里就不再讨论。ANOVA分析的特殊例子就是两组数据分析和比较,一般是F检验方差(Variances),根据方差检验情况用t检验比较均值。
4总结
新的《化学药物(原料药和制剂)稳定性研究技术指导原则》中数据的处理用了一个部分讲数据的统计处理,这也是未来药物生产和质控的趋势(一次好不是真的好,高概率的好才是真的好),其中对数据变异的描述较多,我们认为分析数据变异是一组数据是分析RSD,描述数据的离散程度;多组数据是比较平均值(mean),在比较均值之前先用方差分析,通过比较δ2来判断数据的离散程度是否相同,两组数据用t检验,三组以上用ANOVA。总结来说:对于数据,统计指标有方差(或者标准差)和平均值,我们对数据分析是方差和平均值是否相等的分析来判断数据是否是来自同一个数据总体,数据是否没有差别。
最后回答一下大家的提问,在药物分析板块帖子:怎样计算中间精密度http://bbs.instrument.com.cn/topic/4889112_3#floor_21,有些版友询问中间精密度的计算公式,我在22楼做了回答,因为公式不好编辑我推荐了一本书《Method Validation in Pharmaceutical Analysis》并指明了公式在书中位置,其实两组数据也可以用ANOVA分析,这两篇帖子可以对照着看,希望对大家会有帮助。