保留指数应用16--程序升温恒温段保留指数计算及不同计算办法探讨
保留指数作为气质定性一个强有力的辅助手段,在天然香精油,香气香味材料,香精产品等的分析鉴定中广泛应用。当然应用范围远不止这些。
对于异构体,同系物和结构特征相似的化合物,由于其质谱图非常相似,谱库检索结果匹配度,排列次序都很接近,检索给出的顺序也不一定正确。但它们的保留时间可能会不同,但保留时间只能在特定色谱条件下不变,而保留指数在固定相相同下有可比性。虽然在相同的柱子上和相同的色谱条件下,两个不同的化合物的保留指数有可能相同。但两个化合物同时具有相同的保留指数(或保留时间)和相同的质谱图的不可能性极小。虽然保留时间也可以帮助确认,但保留时间会随着柱子使用的不同阶段新旧等因素而变化,但保留指数是和固定相为主要因素的一个值,相对比较固定不变。所以才有保留指数辅助定性更具有优势。在谱库检索的基础上,用保留指数来确认结果。是一种很重要的手段。
本篇粗略讨论程序升温恒温段的保留指数计算。
附:保留指数基本概念
保留指数retention index或KovatsIndex(RI或KI)概念是由Kovats在1958年提出。是把组分的保留值用两个分别前后靠近它的正构烷烃来标定(这比仅用一个参比物质的相对保留值定向更为精确)。正构烷烃的保留指数规定为等于该烷烃分子中碳原子数的100倍。例如正己烷的RI为600,正庚烷为700,正十五烷为1500.正构烷烃的RI与所用的色谱柱,柱温及其它操作条件无关。
保留指数(RI)的计算公式如下:
I=100Z+100[logt’R(x)-logt’R(z)]/ [logt’R(z+1)- logt’R(z)] (恒温分析) (1)
式中:t’R为校正保留时间;
Z和Z+1分别为目标化合物(X)流出前后的正构烷烃所含碳原子的数目;
这里:t’R(z)< t’R(x)< t’R(z+1), 一般正构烷烃所含碳原子的数目Z大于4.
以上的保留指数(RI)的计算只用于恒温分析。对于沸点范围较宽的复杂组分混合物的分析,一般采用程序升温的方法。在程序升温时,组分的保留指数的测定有所不同。两者有差异,需要校正。
1963年Van Den Dool 等经过推算(详细的推导过程略)引入线性程序升温保留指数的概念。
IT=100Z+100[TR(x)-TR(z)]/[TR(z+1)-TR(z)] (线性程序升温) (2)
式中:TR(x),TR(z),TR(z+1)分别代表组分及碳数为Z,Z+1正构烷的保留温度。且TR(z)R(x)R(z+1)。
一般讲,保留温度的测量比保留时间的测定要麻烦一点。由于保留温度和保留时间通常具有高度的相关性,所以用保留时间代替上式中的保留温度来进行计算保留指数。
IRT=100Z+100[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)] (线性程序升温) (3)
式中:RTR(x),RTR(z),RTR(z+1)分别代表组分及碳数为Z,Z+1正构烷的保留时间。且RTR(z)R(x)R(z+1)。
保留指数与保留时间的转换
从IT=100Z+100[TR(x)-TR(z)]/ [TR(z+1)-TR(z)](3)式可以导出:
TR(x)= [IT-100Z]*[TR(z+1)-TR(z)]/100+TR(z) (4)
(16)程序升温恒温段保留指数计算及不同计算办法探讨
公式(1)是用于恒温情况下的保留指数计算,公式(2)和(3)是用于线性程序升温情况下的保留指数计算。但往往会遇到多阶程序升温的情况,升温过程既有不同的升温速率的线性程序升温又有恒温阶段。
1试验部分
1.1 仪器与装置
美国安捷伦6890N/5973I气相色谱-质谱联用仪。
1.2样品和标样、试剂
所用香气化合物标准品均来自Sigma-Aldrich等主要试剂公司,少数为实验室内部精制标样。C6-C30正构烷混合标准物来自上海安谱。
1.3 gc/MS条件
1.3.1 色谱条件:
色谱柱:HP-Innowax (60m×0. 25 mm ( i.d.)×0.25μm)毛细管柱;
升温程序: 60℃保持0 min,以3 ℃/min升至240℃,保持20 min;
载气(He, 纯度99.999%以上)流速1.9 mL/min;
进样口温度250℃,分流进样,分流比20:1,进样量1ul;
1.3.2质谱条件:
电子轰击(EI)离子源;电子能量70eV;传输线温度280℃;离子源温度230℃;
四级杆温度150℃。SCAN扫描范围:29-400。EMV:1515V。
1.4 标样配制
正构烷混合标准混合物,用正戊烷稀释至约0.05%浓度。
2 结果与讨论
2.1 C6-C30正构烷出峰和程序升温出峰
下面为C6-C30正构烷的总离子色谱图。程序升温:60℃保持0 min,以3 ℃/min升至240℃,保持20 min。
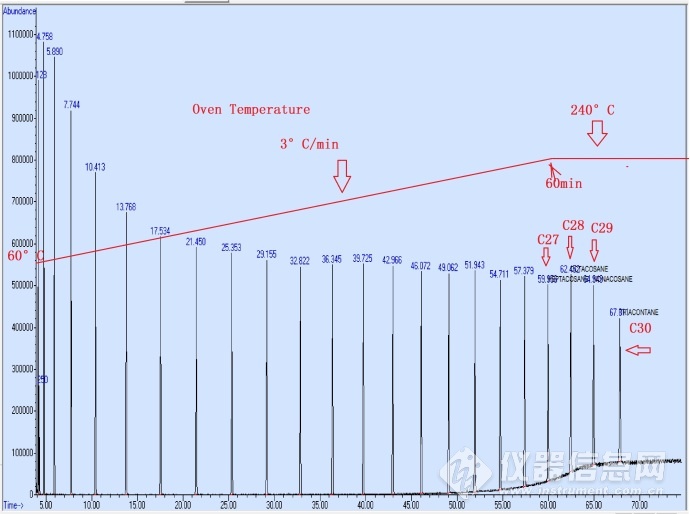
图 C6-C30正构烷的总离子色谱图和程序升温示意图
****************************************************************************************
2.2恒温阶段的保留指数计算
恒温阶段C27-C30正构烷的保留时间和保留温度如下:
表1 恒温阶段C27-C30正构烷的保留时间和保留温度
| 正构烷名称 | 正构烷保留时间(min) | 正构烷保留温度(°C) |
| C27 | 59.956 | 239.87 |
| C28 | 62.452 | 240 |
| C29 | 64.949 | 240 |
| C30 | 67.811 | 240 |
计算保留指数举例。
分别用公式(1)、(2)和(3)来计算保留指数。
程序升温的恒温阶段,理应按照公式(1)来进行保留指数计算,结果参见表2。
公式(2)里面使用保留温度来计算保留指数,在恒温阶段柱温是相同的,保留温度都是一样的,公式的分子和分母都是0,无法进行计算,不适应。
公式(3)本来是计算线性升温的保留指数的,但不妨试试,看看结果怎样,结果参见表2。
表2 三种计算方式计算保留指数结果
| 恒温保留指数 | 线性升温温度保留指数 | 线性升温保留时间保留指数 |
| 化合物名称 | 化合物保留时间(min) | 化合物保留温度(°C) | 式(1)计算保留指数 | 式(2)计算保留指数 | 式(3)计算保留指数 |
| 丁位癸内酯丙二醇反应物1 | 64.513 | 240 | 2882.8 | 不适应 | 2882.5 |
| 丁位癸内酯丙二醇反应物2 | 65.314 | 240 | 2913.0 | 不适应 | 2912.8 |
| 丁位十一内酯丙二醇反应物1 | 67.358 | 240 | 2984.5 | 不适应 | 2984.2 |
| 棕榈酸 | 63.856 | 240 | 2856.7 | 不适应 | 2856.2 |
| Frambinone | 67.794 | 240 | 2999.4 | 不适应 | 2999.4 |
2.3 两种计算方式结果比较
从表2 看出,利用公式(1)恒温保留指数计算公式和利用公式(3)线性升温保留指数计算公式的保留指数居然几乎一样,相差极小,可以忽略不计。两种方法都可以用。有意思,这个是原来没有想到过的。相对于恒温保留指数计算公式(1),线性升温保留指数计算公式(3)更简单一些,可以不用对数来计算。
2.4 恒温保留指数计算公式(1)和线性程序升温计算公式(3)的对比和关系
为什么两种计算办法(计算公式)的保留指数数值几乎一样呢?
纵观公式(1)和(3),粗略看到公式(1)是利用对数进行计算,而公式(3)是普通加减计算。初次感觉不好统一,关系难以看出来。
但把两个公式相除,则出现下面的结果:
{100Z+100[logt’R(x)-logt’R(z)]/ [logt’R(z+1)- logt’R(z)] }/{100Z+100[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)]}
={Z+[logt’R(x)-logt’R(z)]/ [logt’R(z+1)- logt’R(z)] }/{Z+[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)]} (同除以100) (5)
从式(5)可以看出,分子分母Z是相同的,只有后半部分分别是对数和一般数值{[logt’R(x)- logt’R(z)]/[logt’R(z+1)- logt’R(z)] }和{[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)]}。
利用对数公式:

把式(5)的不同部分相除,则
{[logt’R(x)-logt’R(z)]/ [logt’R(z+1)- logt’R(z)] }/{[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)]}
={[logt’R(x)- logt’R(z)]/ [logt’R(z+1)-logt’R(z)] }/{[RTR(x)-RTR(z)]/ [RTR(z+1)-RTR(z)]}
={[logt’R(x)- logt’R(z)]/ [logt’R(z+1)-logt’R(z)] }/{[log 10RTR(x)-log 10RTR(z)]/ log10RTR(z=1)-log 10RTR(z) }
={[logt’R(x)/R(z)]/ [logt’R(z+1)/R(z)]}/{[log 10RTR(x)/10RTR(z)]/ log 10RTR(z=1)/10RTR(z)}
={[logt’R(x)/R(z)]/ [logt’R(z+1)/R(z)]}/{[logtR(x)/R(z)]/ [logtR(z+1)/R(z)]} (都是10的x次方简化)
=1 (6)
把式(6)带入式(5),则:
{100Z+100[logt’R(x)-logt’R(z)]/ [logt’R(z+1)- logt’R(z)] }/{100Z+100[RTR(x)-RTR(z)]/[RTR(z+1)-RTR(z)]}
={Z+1}/{Z+1}=1
这就是为什么两种计算办法(计算公式)的保留指数数值几乎一样的原因。表2中两者方式计算的保留指数数值尾数设置略有差异可能是计算过程数值取舍引起的误差。
以上是程序升温恒温段的保留指数计算的粗略探讨及恒温保留指数计算公式和线性升温保留指数计算公式关系的粗浅探讨。如果不妥,请各位老师批评指正。



