（紫外/可见）吸光光度法讲座（共20讲）

（紫外/可见）吸光光度法讲座（2）

——紫外与可见光吸收光谱的形成



原子或分子中的电子，总是处在某一种运动状态之中。每一种状态都具有一定的能量，属于一定的能级。这些电子由于各种原因（如受光、热、电的激发）而从一个能级转到另一个能级，称为跃迁。当这些电子吸收了外来辐射的能量就从一个能量较低的能级跃迁到一个能量较高的能级。因此，每一跃迁都对应着吸收一定的能量辐射。具有不同分子结构的各种物质，有对电磁辐射显示选择吸收的特性。正像我们在光度分析中经常见到的，有色物质的溶液对不同波长的入射光线有不同程度的吸收。吸光光度法就是基于这种物质对电磁辐射的选择性吸收的特性而建立起来的，它属于分子吸收光谱。分子吸收光谱形成中所吸收的能量与电磁辐射的频率成正比，符合普朗克条件：

ΔE＝E₂－E₁＝hν＝hc/λ （l-28）

ΔE＝ΔE_振＋ΔE_转＋ΔE_电子 （1-29）

（σ）＜（π）＜（n）＜（π^*）＜（σ^*）

吸光光度法（紫外/可见光谱）讲座（3）

——吸光光度法的基本原理及摩尔吸光系数





实验表明，有色溶液对光的吸收程度，与该溶液的液层厚度、浓度以及入射光的强度等因素有关。如果保持入射光的强度不变，则光吸收程度（A）与液层厚度及溶液的浓度有关。
其定量关系式为：

A＝lgI₀/I＝Kcl

式中 I₀——单色光通过待测溶液前的强度；

I——单色光通过待测溶液后的强度；

K——吸光系数，为一常数，其数值与溶液的性质及入射光波长有关；

c——溶液中待测物质的浓度；

l——待测溶液的厚度。

1-30式称作朗伯-比尔定律，它是吸光光度分析的基本原理。这个关系式仅适用于单色光及均匀非散射的液体、固体和气体。

朗伯-比尔定律是由表示液层厚度和光吸收关系的朗伯定律（A＝lgI₀/I＝K₁l）及表示溶液浓度与光吸收关系的比尔定律（A＝lgI₀/I＝K₂l）合并而得。

在朗伯-比尔定律中，如果有色物质溶液浓度单位为mol/L，液层厚度的单位为cm，则公式中的K就可以用摩尔吸光系数ε表示，其单位为L·mol^-1·cm^-1。换言之，摩尔吸光系数就是当有色物质溶液浓度为1mol/L，液层厚度为1cm时的吸光度。

在实际分析工作中，我们不可能直接取1mol/L这样高浓度的有色溶液来测定摩尔吸光系数ε值，而是对适当的低浓度溶液测定吸光度，然后通过计算求出ε值。

例：在用新钴试剂（5-Cl-PADAB）测定钴的标准曲线中，用2cm厚度的吸收皿，在575nm波长处测得Co²⁺为5μg／50mL这一点的吸光度A＝0.383，计算其摩尔吸光系数。

解：Co的相对原子质量为58.93

[Co²⁺]＝（5×10^－6）/（50×58.93）×1000

＝1.70×10^－6（mol/L）

所以 ε＝A/cl＝0.383/（1.70×10^－6×2）

＝1.13×10⁵（L·mol^－1·cm^－1）

应该指出，上面测得的摩尔吸光系数是表观摩尔吸光系数。因为在测定中我们把被测组分看作完全转变成有色化合物进行计算的。实际上，溶液中的有色物质的浓度常因离解等因素而有所改变，但通常不考虑这些变化。

摩尔吸光系数是有色化合物的重要特性，也是鉴别光度法灵敏度的重要标志。它与入射光的波长、溶液的性质和温度、仪器的质量有关，而与溶液的浓度和液层的厚度无关。在一定条件下它是一常数，可以表明有色溶液对某一特定波长光的吸收能力。ε值越大，吸光光度法测定的灵敏度就越高。如以硫氰酸盐测定钴，ε₆₂₀＝1.90×10³，而用新钴试剂测定钴，
ε＝1.13×10⁵，后法比前法的灵敏度提高了50多倍。灵敏的光度法的摩尔吸光系数ε的值通常应在10⁴～10⁵。



图1 产生紫外与可见吸收光谱常见的几种跃迁

（紫外/可见）吸光光度法讲座（4）
——导致偏离朗伯-比尔定律的因素

在吸光光度分析中，导致偏离朗伯-比尔定律的原因很多，但基本上可分为物理和化学两个方面。属于物理原因的主要是入射光的单色性不纯所造成的；化学方面主要是由于溶液本身化学变化造成的。
（1） 单色光不纯引起的偏离
严格说来，朗伯-比尔定律只适用于单色光。但由于仪器分辩能力所限，入射光实际为一很窄波段的谱带，即在工作波长附近或多或少含有其他杂色光。这些杂色光将导致朗伯-比尔定律的偏离。
（2） 溶液本身引起的偏离
溶液本身引起的偏离有以下原因：
1）溶质和溶剂的性质。碘在四氯化碳溶液中呈紫色，在乙醇中呈棕色，在四氯化碳溶液中即使含有1％乙醇也会使碘溶液的吸收曲线形状发生变化。溶液的折光指数（n）随溶液的浓度改变而变化，并对吸光度有影响。当溶液浓度低于0.01mol／L时，n基本上是一常数，这也说明朗伯-比尔定律只有在低浓度中应用才是正确的。
2）介质不均匀性。朗伯-比尔定律是适用于均匀、非散射的溶液的一般规律，如果被测试液是胶体溶液、乳浊液或是浊液，则入射光通过溶液后，除了一部分被试液吸收，还会有反射、散射使光损失，导致透光率减小，吸光度异常增大，造成对朗伯-比尔定律的偏离。
3）溶质的离解、缔合、互变异构及化学变化。离解是偏离朗伯-比尔定律的主要化学因素。溶液浓度的改变，离解程度也会发生变化，吸光度与浓度的比例关系便发生变化，导致偏离朗伯-比尔定律。
溶液中有色质点的聚合与缔合，形成新的化合物或互变异构等化学变化以及某些有色物质在光照下的化学分解、自身的氧化还原、干扰离子和显色剂的作用等，都对遵守朗伯-比尔定律产生不良影响。

吸光光度法（紫外/可见光谱）讲座（5）

——应用吸光光度法测定配合物的组成





用吸光光度法测定配合物的组成是比较简便有效的，这里介绍几种测定有色配合物组成的方法。

1 连续变化法（等摩尔系列法）

此法又称Job法，在实验条件下，将所研究的金属离子M与试剂R配制成一系列浓度比（c_M：c_R）连续变化的，而其总浓度（Q＝c_M＋c_R）相等的溶液。对这一系列溶液，在一定波长下测定其吸光度A，用A作纵坐标，以连续变化的浓度比c_M ：c_R（常用浓度相同的M与R的体积比）为横坐标作图。吸光度最高点相应的横坐标c_M ：c_R（在浓度相同时为体积比V_M ：V_R），即为配合物的组成比。

假设金属离子M和试剂R有如下反应：

aM十bR ＝ M_aR_b

lgy＝a lgm＋b lgn＋lgK

dy/y＝a dm/m＋b dn/n

dy/y＝0

吸光光度法（紫外/可见光谱）讲座（6）

——应用吸光光度法测定配合物的组成

2 平衡移动法

在一系列相同体积的容量瓶中，加入一定量的金属离子M，以及逐点增量的显色剂R（保持M尚未全部形成配合物），显色定容使反应达到平衡，相对于各自的空白测量这一系列溶液的吸光度。在另一同体积容量瓶中，加入同样量M，过量的显色剂R，以便使M最大限度地被R配合，然后相对其空白测定最大吸光度A_max，以lg [A_i /（A_max－A_i）]对lg[R]作图，所得直线斜率即为配合比。这种方法称为平衡移动法又叫做有限对数法。此法对离解度较大的配合物以及可形成几种配合物的体系，也能得到满意的结果，因此应用较广。

假设配合平衡为

M＋nR ＝ MR_n

K_稳＝[MR_n] /（[M][R]ⁿ）

lg（[MR_n] / [M]）＝lgK_稳＋n lg[R]

吸光光度法（紫外/可见光谱）讲座（7）

——应用吸光光度法测定配合物的组成



3 摩尔比法

摩尔比法也称饱和法。此法是根据在配合反应中金属离子M被显色剂R所饱和的原理来测定配合物的组成的。

在实验条件下，我们制备一系列体积相同的溶液。在这些溶液中，固定金属离子M的浓度，依次从低到高地改变显色剂R的浓度，然后测定每份溶液的吸光度A，随着[R]的加大，形成配合物的浓度[MR_n]也不断增加，吸光度A也不断增加，当[R] ：[M]＝n时，[MR_n]最大，吸光度也应最大。这时M被R饱和，若[R]再增大，吸光度A即不再有明显增加。用测得的吸光度对[R] / [M]作图，所得曲线的转折点相对应的[R] / [M]值，即为配合物的组成比。
用摩尔比法可以求配合物MRn的稳定常数K稳，其反应式为
M＋nR＝MRn
K稳＝[MRn] /（[M][R]n）
当金属离子M有一半转化为配合物MRn时，即[MRn]＝[M]，则
K稳＝1 / [R]n （1-33）
因此，只要取摩尔比法曲线的最大吸光度的一半所对应的[R]，并将已求得的n代入，即可求得配合物的稳定常数K稳。

吸光光度法（紫外/可见光谱）讲座（8）
——应用吸光光度法测定配合物的组成

4 斜率比法
它是利用两条直线的斜率之比来测定配合物的组成。主要用来测定离解度小的配合物。
如果溶液中只存在下述反应：
aM十bR＝MaRb
先固定R的浓度，并保证过量，加入少量不同浓度的M，则配合物MaRb的平衡浓度与加入溶液中M的浓度cM成正比：
[MaRb]＝cM / a
A＝εl[MaRb]＝εl cM / a
以A对CM作图，就得到一条斜率为S1的直线：
S1＝εl / a
同理，如果保持M大量过剩并固定浓度，改变R的浓度，则得到一条斜率为S2的直线：
S2＝εl / b
S2 / S1＝（εl / b）/（εl / a）＝a / b （1-34）
因此，两直线斜率之比，就是配合物的组成比a / b。

吸光光度法（紫外/可见光谱）讲座（9）
——应用吸光光度法测定配合物的组成

5 直线法
此法又称阿斯马斯（Asmus）法。在一系列容量瓶中，加入固定量的金属离子M的标准溶液，加入不同体积V的试剂R的溶液。在实验条件下，显色，定容，测定吸光度A。根据阿斯马斯的计算，对形成MRb型配合物来说，加入试剂R的体积V的b次方之倒数与其吸光度A的倒数成直线关系。
对于下列平衡
aM十bR＝MaRb
K不稳＝[M]a[R]b / [MaRb]
[M]a[R]b＝K不稳[MaRb] （1-35a）
当达到平衡时，溶液中有
[M]＝cM－a[MaRb] （l-35b）
[R]＝cR－b[MaRb]
由朗伯-比尔定律得
[MaRb]＝A /εl （1-35c）
由式1-35a、b、c得
（cM－a×A /εl ）a[R]b＝K不稳×A /εl （1-35d）
当a＝1时，即为MRb型配合物，整理式1-35d得
1 / [R]b＝εlcM / K不稳×1 / A－1 / K不稳 （1-35e）
式1-35e中，K不稳、ε、l、cM在实验条件下，均为常数，且[R]与其加入的体积V成正比，则式1-35e可写为：
1 / Vb＝α×1 / A－β （1-35f）
式中 α＝εlcM / K不稳，β＝1 / K不稳
将式1-35f改写成一般函数式：
1 / Vb＝f×1 / A （1-35g）
令b＝1，2，3，…，用1 / Vb对1 / A作图，得出数条曲线，其中为直线的一条，其相应的b即为配合物中R与M之比。

吸光光度法（紫外/可见光谱）讲座（10）
——提高吸光光度法灵敏度和选择性的某些途径

1.2.5.1 示差吸光光度法
示差吸光光度法是用一已知浓度的标准显色溶液与未知试样的显色溶液相比较，测量吸光度，从测得的吸光度求未知浓度。
设标准溶液的浓度为c，试样溶液的浓度为cx，则
A0=-－lg(I/I0)=abc
Ax=-－lg(Ix/I0)=abcx

lgI0－lgI＋lgIx－lg I0＝abc－abcx
lgIx－lg I＝ab（c－cx）
A差＝－lg（Ix / I）＝ab（c－cx） （1-36）
以A差对（c－cx）作图，可以求出c－cx，c为已知，则cx可求得。按所选择测量条件
不同，示差吸光光度法有三种操作方法：
（l）高吸光度法。光电检测器未受光时，其透光度为零，光通过一个比试样溶液稍稀的参比溶液后照到光电检测器上，调其透光度（T）为100％，然后测定试样溶液的吸光度。此法适用于高含量测定。
（2）低吸光度法。先用空白溶液调透光度为100％，然后用一个比试样溶液稍浓的参比溶液，调节透光度为零，再测定试样溶液的吸光度。此法适用于痕量物质的测定。
（3）双参比法。选择两个组分相同而浓度不同的溶液作参比溶液（试样溶液浓度应介于两溶液浓度之间），调节仪器，使浓度较大的参比溶液的透光度为零，而浓度较小的参比溶液的透光度为100％，然后测定试样溶液的吸光度。
示差吸光光度法可以提高光度法的精确性，从而实现用吸光光度法对物质中某一含量较高或较低的组分的测定。例如对高含量成分的测定，有时可达到与重量法、滴定法同等的精确度。其降低分析误差的主要依据就是对刻度标尺的放大作用。例如，假定用普通光度法测量参比溶液的透光度为10％，试样溶液的透光度为 7％，仅相差 3％。若用示差法，将参比溶液的透光度调到100％，则试样溶液的透光度为70％，两者之差增为30％，相当于放大读数标尺10倍。从而相对地增大了这种测量方法的精确性（图1-4）。
在示差吸光光度法的测量中，要求一个实际具有较高吸收的参比溶液的表观刻度读数为A＝0或T＝100％，故所用的仪器必须具有出光狭缝可以调节，光度计灵敏度可以控制或光源强度可以改变等性能。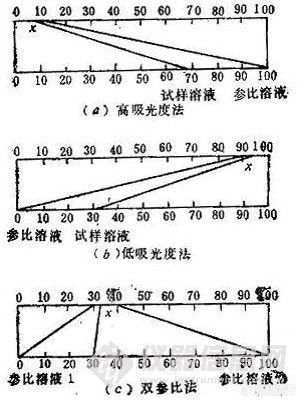

图1-4 不同测量方法的示差吸光光度法的精确性