

标准曲线对原吸测定的重要性是毋庸置疑的。只有好的标准曲线才能准确地表达待测元素的浓度与测试信号值的关系。也只有这样,我们才能根据样品溶液的测试信号值计算出样品的准确含量。原吸测定过程中产生的误差随处可见,相对于极微量的样品含量,样品结果那狭小的波动范围实在是太容易“出轨”了。这一点做过考核样的同行们相信都深有体会。正所谓“差之毫厘,谬以千里”,当我们拿样品的吸光度值去求结果浓度时,标曲方程准确性的重要性是不言而喻的。但是关于标曲方程,你又知道多少呢?老老实实,按部就班地去做检样,是不是就可以高枕无忧了?答案是NO! 请先看下文。我保证,下面所说的一切都是事实。
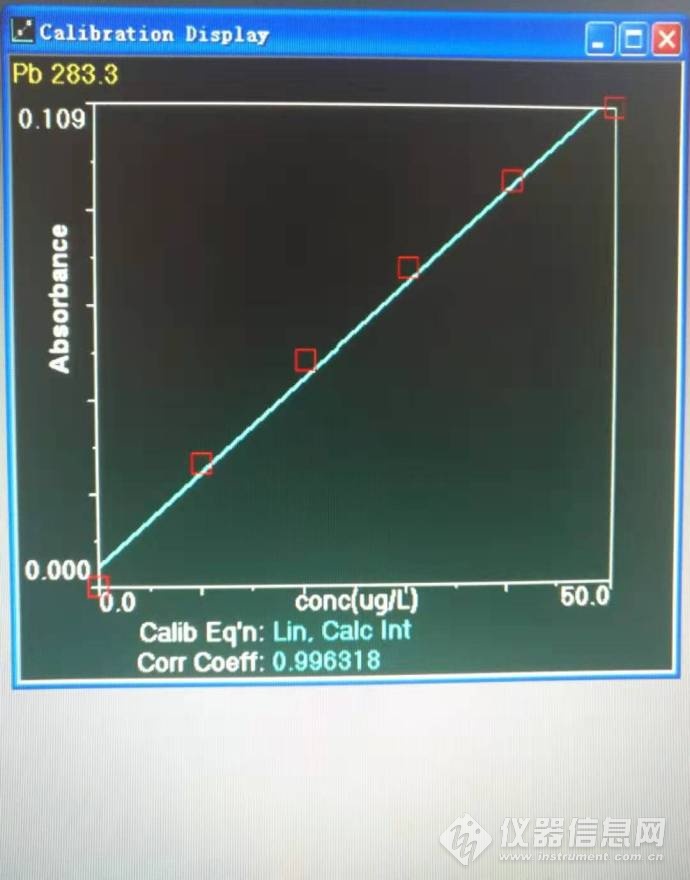
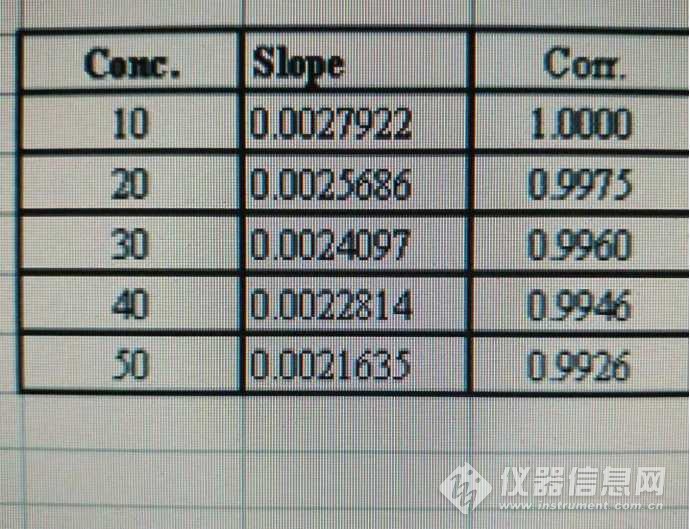
图1 线性标准曲线
这是一条普通的铅标准曲线。它太普通了,普通到我都没有什么话好讲。哦,我选择的是线性方程,它的回归系数有点低!
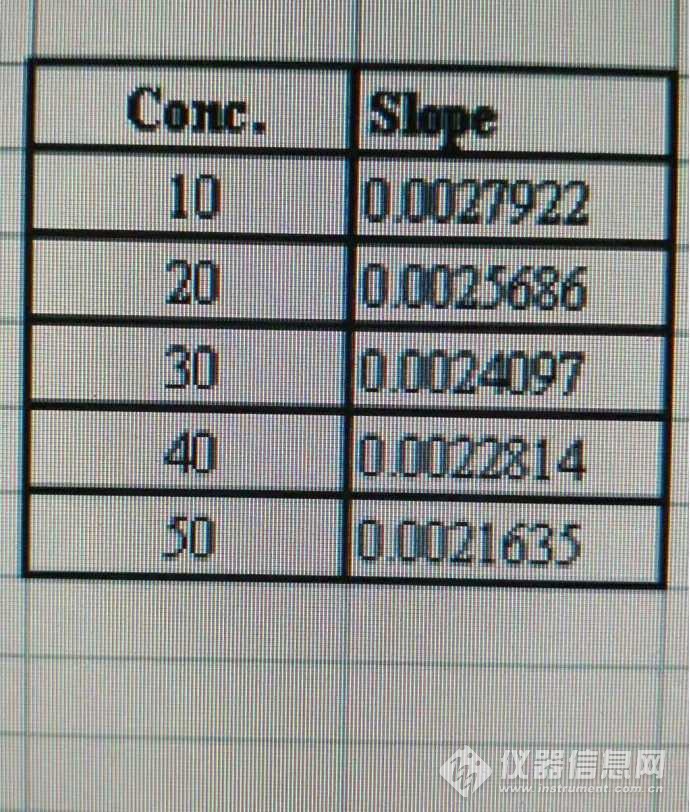
图2 标曲的逐点斜率
逐点斜率,这个是我给它起的名,所以需要亲自解释一下。逐点斜率,就是标曲从零点开始,做到某点时标曲的斜率。比如,Conc.:10,Corr.: 0.0027922这一组数据的意思是当只有零点和10ug/L这两个点时标曲的斜率,Conc.:20,Corr.: 0.0025686这一组数据是指包括零点、10ug/L和20ug/L这三个点时标曲的斜率,以此类推。。。从图2可以看出,逐点斜率越来越低,这说明标曲不是一条直线,而是逐渐弯曲,也即大家常说的“弯头”现象。
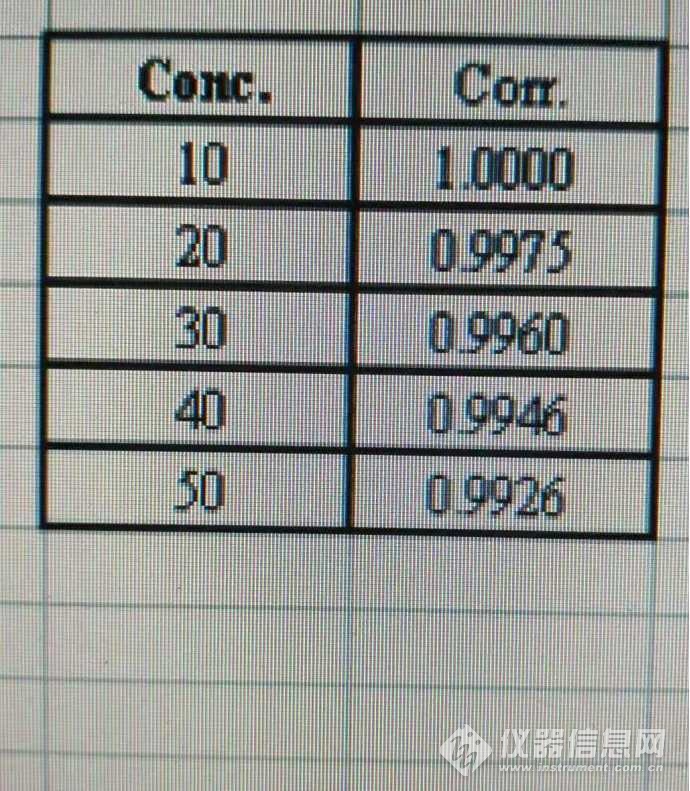
图3 标曲的逐点回归系数
逐点回归系数,与上面的逐点斜率一样,也是我起的名,意思也跟上面一样,就是标曲从零点开始,做到某点时标曲的回归系数。从图3可知,逐点回归系数越来越低,显示标曲的不确定度越来越大,标曲方程越来越不能准确反映标液浓度与吸光度值之间的关系。
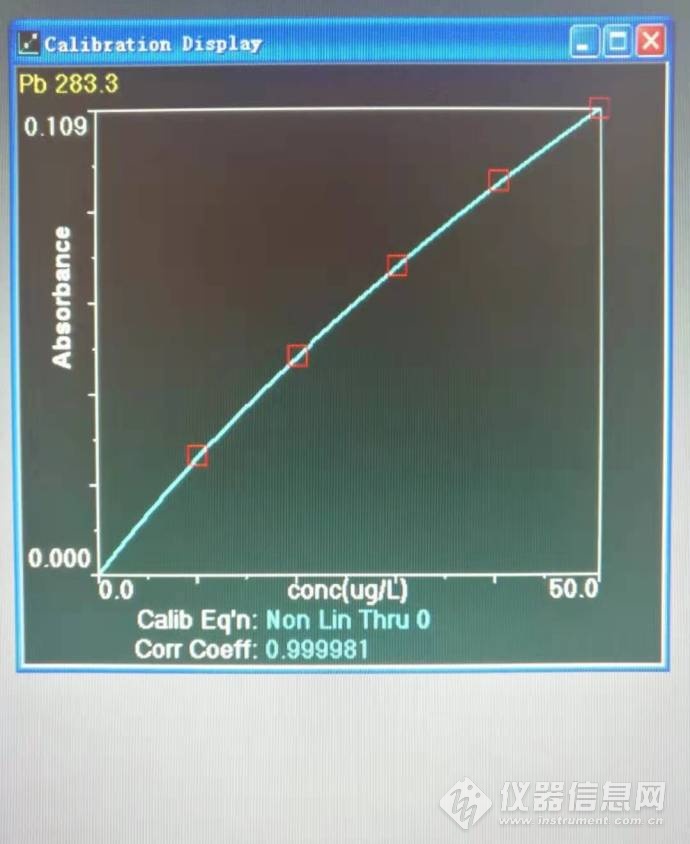
图4 非线性标准曲线
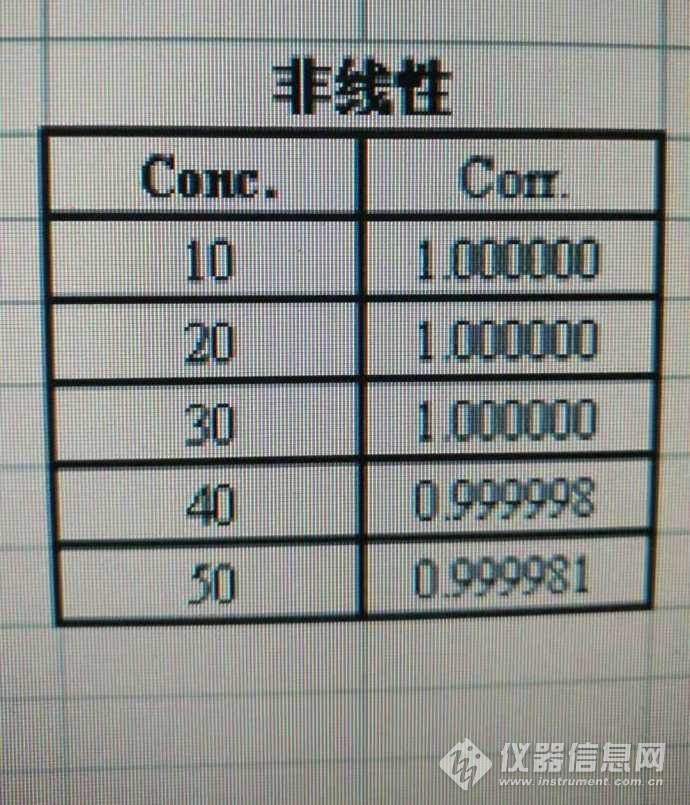
图5 非线性标曲的逐点回归系数
与上面的线性标准曲线所用的是同样的数据,但这一次我选择非线性标曲。从图5来看,非线性标曲的逐点回归系数要比线性的好很多,表明该方程更能准确反映标液浓度与吸光度之间的关系,也就是说,用这样的方程计算出来的样品溶液的浓度会更准确。
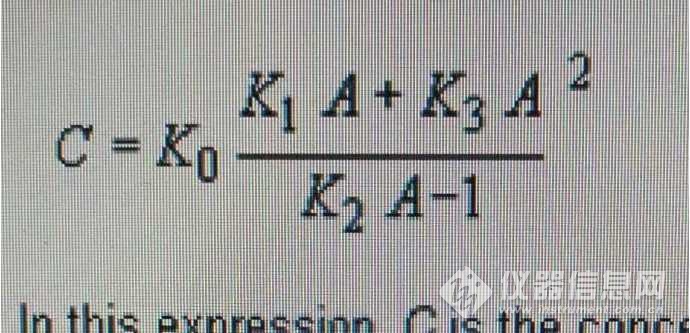

图6 非线性方程
上图即是非线性方程。我在EXCEL做图时,只能选用二阶方程来描述曲线,上面的公式才是正宗的非线性方程,这是我从PE的工作软件里找出来的。
再看下面的数据就更清楚了:
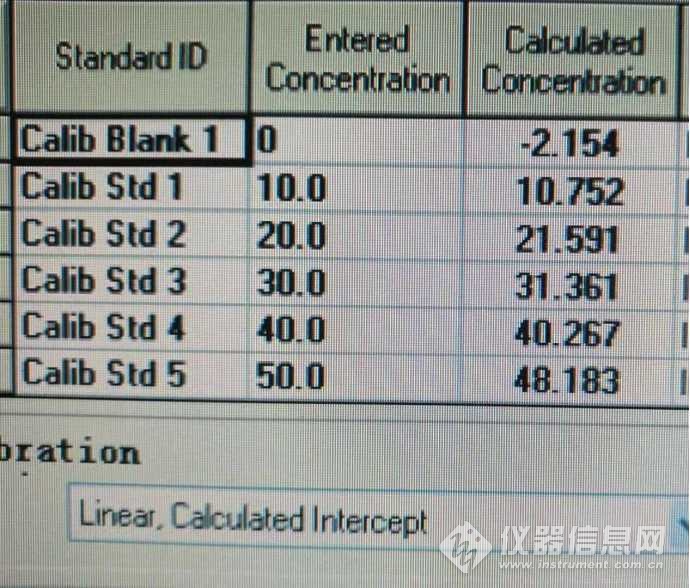
图7 线性截距标曲方程 计算浓度与实际浓度对比
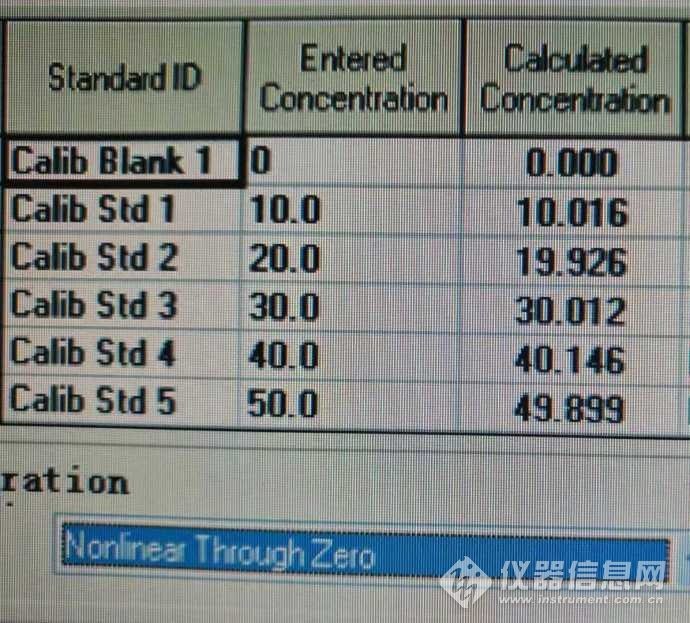
图8 非线性标曲方程 计算浓度与实际浓度对比
大家都知道,样品浓度最好要在标曲的中间位置,这样得到的结果是最准确的。这一点,从图7、图8两图可以看出来。30ug/L这个位置点的计算浓度与实际浓度相差是最小的。从两图中还可以看出,采用不同的标曲方程得到的计算浓度与实际浓度之间相差较大,非线性标曲方程的计算结果明显要优于线性截距标曲方程。
以上是我近来偶然所得。由于本人水平有限,不当之处在所难免,在此,真诚愿与大家探讨。
冰山
第10楼2019/07/25
本来我是笃信线性方程的,可看了图2逐点斜率以后改变了想法。除非线性方程外,PE的校准方程中还有一种"linear,bracting",把零点舍去,在某些情况下不过零点得到的方程线性相关系数更好。朗伯比尔公式A=KCT只是一个近似式,只在浓度低且较小范围内适应。有种想法,似乎标曲点越多越好,样品测试液的信号值出来以后直接找相同或接近的标液数据,从而得到浓度值。不用靠方程计算样品测试液的浓度,这样才准确。不然,看标曲计算结果,明明是10ug/L,算出来的却是10.752ug/L,多冤!可好象说关非标曲上点越多越好